Главная страница
Навигация по странице:

  • H0={Распределение нормальное}

  • Справедливо предположение о том, что данные выборки имеют нормальное распределение.

    		•

    проверка статистических гипотез. 8.2. Проверка статистической гипотезы (3). 8 Проверка статистической гипотезы о виде неизвестного распределения Задание


    Скачать 58.76 Kb.
    Название8 Проверка статистической гипотезы о виде неизвестного распределения Задание
    Анкорпроверка статистических гипотез
    Дата06.01.2023
    Размер58.76 Kb.
    Формат файлаdocx
    Имя файла8.2. Проверка статистической гипотезы (3).docx
    ТипДокументы
    #874000
    страница4 из 4
    1   2   3   4

    7. Проверка гипотез о виде распределения.

    Выдвинем гипотезу: H0={Распределение нормальное}

    1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.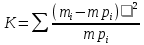



    где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону

    Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа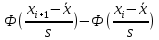



    где

    s = 0.922, xср = 0.0958

    Теоретическая (ожидаемая) частота равна mi = mpi, где m = 100

    Вероятность попадания в i-й интервал: pi = Ф(x2) - Ф(x1)

    xi÷xi+1
    mi
    x1 = (xi - xср)/s
    x2 = (xi+1 - xср)/s
    Ф(x1)
    Ф(x2)
    pi=Ф(x2)-Ф(x1)
    Ожидаемая частота, 100pi
    Слагаемые статистики Пирсона, Ki

    -2.42 - -1.821
    3
    -2.7145
    -2.0682
    -0.4967
    -0.4812
    0.0155
    1.55
    1.3565

    -1.821 - -1.222
    7
    -2.0682
    -1.4219
    -0.4812
    -0.4236
    0.0576
    5.76
    0.2669

    -1.222 - -0.623
    9
    -1.4219
    -0.7756
    -0.4236
    -0.2823
    0.1413
    14.13
    1.8625

    -0.623 - -0.024
    23
    -0.7756
    -0.1293
    -0.2823
    -0.0517
    0.2306
    23.06
    0.000156

    -0.024 - 0.575
    28
    -0.1293
    0.5171
    -0.0517
    0.1985
    0.2502
    25.02
    0.3549

    0.575 - 1.174
    18
    0.5171
    1.1634
    0.1985
    0.379
    0.1805
    18.05
    0.000139

    1.174 - 1.773
    10
    1.1634
    1.8097
    0.379
    0.4649
    0.0859
    8.59
    0.2314

    1.773 - 2.372
    2
    1.8097
    2.456
    0.4649
    0.4931
    0.0282
    2.82
    0.2384




    100












    4.311

    Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы.

    Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).

    Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры xcp и s оценены по выборке).

    Kkp = χ2(8-2-1;0.05) = 11.07050; Kнабл = 4.31

    Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу.

    Справедливо предположение о том, что данные выборки имеют нормальное распределение.


    1   2   3   4

    написать администратору сайта