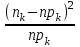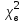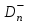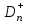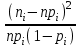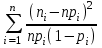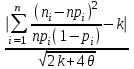Практ.раб 4.к надеж.Эмпир.. Построение кривой нормального распределения по опытным данным. Проверка гипотезы о нормальном распределении выборки
 Скачать 378.01 Kb. Скачать 378.01 Kb.
|
Практическая работа 4Построение кривой нормального распределения по опытным данным. Проверка гипотезы о нормальном распределении выборки (лекция 4) Содержание работы: Проверка статистических гипотез включает в себя большой пласт задач математической статистики. Зная некоторые характеристики выборки (или имея просто выборочные данные), мы можем проверять гипотезы о виде распределении случайной величины или ее параметрах (примеры этих задач на странице Проверка гипотез о параметрах распределения).Ниже в примерах разбираются основные учебные задачи на проверку гипотез о виде распределения. Чаще всего для этого используется критерий согласия χ2χ2 Пирсона, а также критерий Колмогорова-Смирнова. Критерий согласия Пирсона (или критерий χ2χ2 - "хи квадрат") - наиболее часто употребляемый для проверки гипотезы о принадлежности некоторой выборки теоретическому закону распределения (в учебных задачах чаще всего проверяют "нормальность" - распределение по нормальному закону). В учебных задачах обычно используется следующий алгоритм: Выбор теоретического закона распределения (обычно задан заранее, если не задан - анализируем выборку, например с помощью гистограммы относительных частот, которая имитирует плотность распределения). Оцениваем параметры распределения по выборке (для этого вычисляется математическое ожидание и дисперсия): a,σa,σ для нормального, a,ba,b - для равномерного, λλ - для распределения Пуассона и т.д. Вычисляются теоретические значения частот (через теоретические вероятности попадания в интервал) и сравниваются с исходными (выборочными). Анализируется значение статистики χ2χ2 и делается вывод о соответствии (или нет) теоретическому закону распределения. Основная задача работы проверить согласованность эмпирического распределения с теоретическим нормальным, применяя критерии и гипотезы: 1.О нормальном распределении 2.О распределении по закону Пуассона 3. О распределении по показательному закону 4.О распределении по равномерному закону 5. По критерию Колмогорова 6. По критерию Колмогорова-Смирнова 7. по критерию Вилкоксона 8.Проверка гипотезы по критерию 2 1. Проверка согласованности эмпирической функции с теоретическим нормальным распределением 1) Критерий Пирсона Покажем, как применять данный критерий в двух случаях: а) без объединения интервалов и б) с объединением интервалов, в которые попало менее 5 значений а) Вычисляем статистику критерия хи-квадрат: 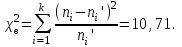 Для уровня значимости α=0.95 и числе степеней свободы l=k-r=8-3=5по Приложению 4, входом к которую является p=1-α=0.05 и K=l=5, находим критическое значение 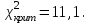 Условием принятия гипотезы о нормальном распределении является условие 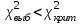 , которое выполняется. Гипотезу о соответствии данного распределения нормальному закону распределения принимаем. , которое выполняется. Гипотезу о соответствии данного распределения нормальному закону распределения принимаем.б) Подробнее покажем, как вычисляется статистика критерия в случае объединения интервалов, содержащих малое количество эмпирических частот. Исходные данные:
*Примечание. Числа -5 и 5 как левый конец первого и правый конец последнего интервалов взяты вместо -∞ и ∞ соответственно для подсчета вероятности попадания в эти интервалы. После объединения интервалов, содержащих малочисленные эмпирические частоты получаем
*Примечание. Для подсчета вероятности попадания в соответствующий интервал использовалась статистическая функция Excel НОРМРАСП. Например, для подсчета вероятности попадания в первый из интервалов, в соответствующую ячейку вводилась формула =НОРМРАСП(G4;$D$12;$C$23;ИСТИНА)-НОРМРАСП(F4;$D$12;$C$23;ИСТИНА), где G4 и F4 – адреса ячеек, в которых находятся соответственно правая и левая границы интервала, $D$12 – адрес ячейки, в которой находится 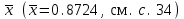 ,$C$23 – адрес ячейки, вкоторой находится смещенная оценка σ (S=0.054279, см. с.34). ,$C$23 – адрес ячейки, вкоторой находится смещенная оценка σ (S=0.054279, см. с.34).По заданному уровню значимости α=0.05 и f=5-2-1=2 степеням свободы с помощью статистической функции ХИ2ОБР(J12;H13), первый аргумент которой – адрес ячейки, содержащей значение уровня значимости, второй – адрес ячейки, содержащей число степеней свободы, находим 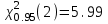 . Так как . Так как 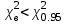 , гипотезу о нормальном распределении генеральной совокупности принимаем. , гипотезу о нормальном распределении генеральной совокупности принимаем.2) Критерий Романовского Воспользуемся результатами предыдущих расчетов. а) для случая без объединения интервалов: 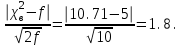 б) для случая с объединением интервалов, в которые попало менее 5 значений: 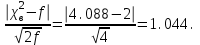 Условием принятия гипотезы о нормальном распределении является условие 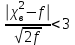 , которое выполняетсяв обоих случаях. , которое выполняетсяв обоих случаях.Гипотезу о соответствии данного распределения нормальному закону распределения принимаем. 3) Критерий Колмогорова-Смирнова По несгруппированной выборке находим 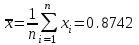 и и 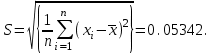
Теоретическая функция распределения F(xcp,S) вычислялась с помощью статистической функции НОРМ. РАСП. Так, первое значение этой функции равно F(x1)=P(X<x1)=НОРМ.РАСП(A6;$C$3;$C$2;ИСТИНА) где A6 – адрес ячейки, содержащей первое значение х1;$C$3 – адрес ячейки, содержащей значение 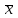 ;$C$2 – адрес ячейки, содержащей значение S. ;$C$2 – адрес ячейки, содержащей значение S.По двум последним столбцам таблицы определяем Dn. Dn=max(0.065262; 0.111368)= 0.111368. В качестве статистики критерия используется величина 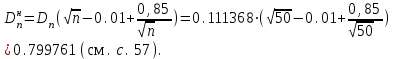 Критические точки взяты из таблицы (см. с. 58). Так, для α=0.05 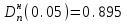 . Так как . Так как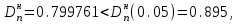 гипотеза о нормальном распределении не отклоняется. гипотеза о нормальном распределении не отклоняется.Критерий Колмогорова для сгруппированной выборки: Критическое значение статистики Колмогорова подсчитывается по формуле: 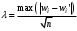 . .Для нахождения максимума абсолютного значения разности между накопленными эмпирическими и теоретическими частотами |wi- wi'| построим таблицу
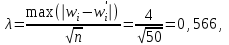 K(λ)= 0,9228 Гипотеза о нормальном распределении принимается, еслиK(λ)>0.05.Это условие выполняется. Гипотезу о соответствии данного распределения нормальному закону распределения принимаем. Критерий Ямстремского 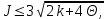 где где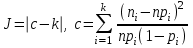 , , ni– эмпирические частоты, 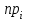 - теоретические частоты,k– число интервалов дискретного вариационного ряда, n- объем выборки. - теоретические частоты,k– число интервалов дискретного вариационного ряда, n- объем выборки. Так как k<20, то Θ=0,6. а) без объединения интервалов: Обозначим 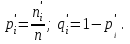 Для вычисления величины c составляем таблицу. Теоретические частоты взяты со с. 68. Для вычисления величины c составляем таблицу. Теоретические частоты взяты со с. 68.
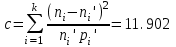 . .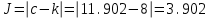 . .Условие принятия гипотезы о нормальном распределении (т.е. 3.902≤12.8686) выполняется. б) для случая с объединением интервалов, в которые попало менее 5 значений, имеем:
Поскольку 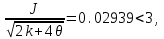 гипотеза о нормальном распределении экспериментальных данных принимается. гипотеза о нормальном распределении экспериментальных данных принимается.5) Приближенный критерий Средние квадратические отклонения асимметрии и эксцесса вычисляют по формулам: 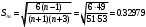 . .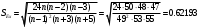 . .Условием принятия гипотезы о нормальном распределении являются условия 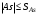 (0.279<0.32979) и (0.279<0.32979) и 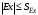 (0.293<0.62193).Оба условия выполняются. (0.293<0.62193).Оба условия выполняются.Вывод: гипотезу о соответствии данного распределения нормальному закону распределения принимаем. Задачи: |