Практ.раб 4.к надеж.Эмпир.. Построение кривой нормального распределения по опытным данным. Проверка гипотезы о нормальном распределении выборки

• Название: Построение кривой нормального распределения по опытным данным. Проверка гипотезы о нормальном распределении выборки
• Дата: 06.12.2021
• Размер: 378.01 Kb.
• Имя файла: Практ.раб 4.к надеж.Эмпир..docx
• Тип: Лекция; #293612
• страница: 5 из 9

Проверка гипотезы по критерию Колмогорова-Смирнова

ЗАДАНИЕ.

В течение месяца выборочно осуществлялась проверка торговых точек города по продаже овощей. Результаты двух проверок по недовесам покупателям одного вида овощей приведены в таблице:



Можно ли считать при уровне значимости 0,05, что недовесы овощей являются устойчивым и закономерным процессом при продаже овощей в данном городе (т.е. описываются одной и той же функцией распределения)?

РЕШЕНИЕ.

Используем критерий Колмогорова-Смирнова (проверяем гипотезу

^{H0 : F1}  ^x ^{ F2}  ^x ^{- о}

том, что данные описываются одной и той же функцией распределения). Вычислим накопленные частоты для обоих выборок и значения эмпирических функций (относительные накопленные частоты). Расчеты будем вести в таблице.

интер- вал	n1	n2	níàê 1	níàê 2	* níàê F1  x 1 n1	* níàê F2  x 2 n2	F*  x  F*  x 1 2
1	3	5	3	5	0,027	0,050	0,023
2	10	12	13	17	0,118	0,170	0,052
3	15	8	28	25	0,255	0,250	0,005
4	20	25	48	50	0,436	0,500	0,064
5	12	10	60	60	0,545	0,600	0,055
6	5	8	65	68	0,591	0,680	0,089
7	25	20	90	88	0,818	0,880	0,062
8	15	7	105	95	0,955	0,950	0,005
9	5	5	110	100	1,000	1,000	0,000

Найдем наибольшее отклонение, затем вычисляем значение критерия:

^{  max F*}  ^x ^{ F*}  ^x ^{  0, 089   0, 644 .}

_xi 1 2

Так как

  _0,05  1, 36 , то гипотеза принимается, можно считать, что недовесы овощей

описываются одной и той же функцией распределения.

Проверка гипотезы по критерию Вилкоксона

ЗАДАНИЕ.

Имеется выборка прибыли коммерческой фирмы за 14 недель до (х_i) и после (y_i)проведения новой экономической политики. На уровне значимости α = 0,05 по критерию Вилкоксона проверить гипотезу о том, что введение новой экономической политики в среднем привело к увеличению производительности.

Вар.№		Выборка
8	х	52	51	48	52	54	50	51	51	52	52	53	56	51	50
	y	44	47	57	54	39	65	46	51	58	46	62	52	65	47

РЕШЕНИЕ.

Вычислим разности наблюдений, абсолютные значения разностей и ранги последних значений. Результаты занесем в таблицу:

x	y	y x	y x	ранг
52	44	-8	8	9
51	47	-4	4	4,5
48	57	9	9	10,5
52	54	2	2	2
54	39	-15	15	13,5
50	65	15	15	13,5
51	46	-5	5	6
51	51	0	0	1
52	58	6	6	7,5
52	46	-6	6	7,5
53	62	9	9	10,5
56	52	-4	4	4,5
51	65	14	14	12
50	47	-3	3	3

Найдем эмпирическое значение критерия (сумму рангов для тех наблюдений, где была замечена неправильная тенденция, в данном случае уменьшение производительности, эти значения выделены жирным в таблице).

Получаем T_эмп 4, 5 13, 5  6  7, 5  4, 5  3  39 .

Найдем критическое значение критерия для уровня значимости

  0, 05

и числу

кр
наблюдений n 14 из таблицы, T 25 .

Так как эмпирическое значение больше критического, нельзя утверждать, что производительность увеличилась.

Проверка гипотезы по критерию  ²

ЗАДАНИЕ.

Используя критерий «хи-квадрат» при уровне значимости α = 0,05, проверить, существует ли зависимость уровня интеллектуального развития учеников от типа школы по результатам обследования 100 сельских и 100 городских школьников:

Тип школы	Уровень интеллектуального развития
	низкий	нормальный	высокий
Городская	25	50	25
Сельская	52	41	7

РЕШЕНИЕ. Заполним таблицу до конца, подсчитывая суммы по столбцам и строкам:

Тип школы	Уровень интеллектуального развития
	низкий	нормальный	высокий	Сумма
Городская	25	50	25	100
Сельская	52	41	7	100
Сумма	77	91	32	200

Вычислим теоретические частоты. Для этого вычислим долю школьников с низким, нормальным и высоким развитием в выборке:

p₁ 

77

200

 0, 385 ,

p₂ 

91

200

 0, 455 ,

p₃ 

32

200

 0,16 .

Теперь вычисляем теоретические частоты, зная значения долей и количество учебников в каждой школе (100 человек):

Тип школы	Уровень интеллектуального развития
	низкий	нормальный	высокий	Сумма
Городская	38,5	45,5	16	100
Сельская	38,5	45,5	16	100
Сумма	77	91	32	200

Суммы по всем строкам и столбцам должны остаться те же, что подтверждает правильность расчетов.

Теперь находим величину

 ² :


^{25  38, 5}2 ^{52  38, 5}2 ^{50  45, 5}2 ^{41 45, 5}2

2

íàáë

    

38, 5 38, 5 45, 5 45, 5

^{25 16}2 ^{7 16}2

   20, 48.

16 16

Критическое значение при

^{v } ^k1^c1 ^{ 1 2  2}

и уровне значимости 0,05 равно 6,0.

Так как наблюдаемое значение больше критического, следует принять гипотезу наличии различий между двумя эмпирическими распределениями.

H₁ о

Другими словами, существует зависимость уровня интеллектуального развития учеников от типа школы (для городской школы уровень развития выше).

0,597	0,6714	0,075
0,865	0,8286	0,036
0,975	0,9571	0,018
0,998	1,0000	0,002

Так как

  
0,05

 1, 36 , то распределение можно считать нормальным на уровне

значимости 0,05.

0	403	0,40657	406,57	12,7449	0,031347
1	370	0,36591	365,91	16,7281	0,045716
2	167	0,16466	164,66	5,4756	0,033254
3	46	0,0494	49,4	11,56	0,234008
4	12	0,01111	11,11	0,7921	0,071296
5	2	0,002	2	0	0
				Сумма	0,416

Из расчетной таблицы находим наблюдаемое значение критерия Пирсона

 ²  0, 416 .

Критическая точка для уровня значимости 0,05 при количестве степеней свободы

k 6  2  4

(число групп минус два) равна 9,5. Так как наблюдаемое значение критерия

0,416 меньше критического значения 9,5, следует принять нулевую гипотезу о распределении генеральной совокупности по закону Пуассона

xi	ui	 (ui )	n 0 i	ni	(n  n0 )2 i i n0 i
0,3	-1,930	0,062	5,204	7	0,620
0,5	-1,528	0,124	10,422	9	0,194
0,7	-1,126	0,212	17,762	28	5,901
0,9	-0,725	0,307	25,760	27	0,060
1,1	-0,323	0,379	31,793	30	0,101
1,3	0,079	0,398	33,390	26	1,636
1,5	0,481	0,355	29,842	21	2,620
1,7	0,882	0,270	22,697	25	0,234
1,9	1,284	0,175	14,689	22	3,638
2,1	1,686	0,096	8,090	9	0,102
2,3	2,087	0,045	3,792	5	0,385
Сумма					15,491

₂ ¹¹ (n 

Наблюдаемое значение критерия вычислим по формуле

_набл  _^{i i}  15, 491.

n
0



i1 _i

По таблице критических значений

² при уровне значимости   0, 05

и числе степеней

кр
свободы

k l 3  11 3  8

найдем

 ²  15, 507 . Так как  ²  15, 491   ²

 15, 507 ,

кр набл кр

нулевую гипотезу о нормальном распределении можно принять при данном уровне значимости.

Проверка гипотезы о нормальности распределения

ЗАДАНИЕ.

Были исследованы 200 готовых деталей на отклонения истинного размера от расчетного. Сгруппированные данные приведены в следующей таблице:

Границы интервалов в микронах	-20 ÷ -10	-10 ÷ 0	0 ÷ 10	10 ÷ 20	20 ÷ 30
Число деталей с данной величиной отклонения	19	42	71	56	12

По данному статистическому ряду построить гистограмму. По виду гистограммы выдвинуть гипотезу о виде закона распределения (например, предположить, что исследуемая величина имеет нормальный закон распределения). Подобрать параметры закона распределения (равные их оценкам на основе опытных данных). На том же графике построить функцию плотности вероятности, соответствующую выдвинутой гипотезе. С помощью критерия согласия проверить, согласуется ли гипотеза с опытными данными. Уровень значимости взять, например, равным 0,05.

РЕШЕНИЕ. Построим гистограмму частот, для чего дополнительно вычислим плотность

частот

p ⁿⁱi <sub>h

</sub> n_i

10

. Получаем:

xi	-20 ÷ -10	-10 ÷ 0	0 ÷ 10	10 ÷ 20	20 ÷ 30
ni	19	42	71	56	12
pi	1,9	4,2	7,1	5,6	1,2

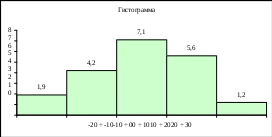По виду гистограммы можно предположить, что исследуемая величина имеет нормальный закон распределения.
Найдем точечные оценки параметров распределения. Для этого перейдем к простому вариационному ряду, выбирая в качестве вариант середины интервалов, составим расчетную таблицу:

xi	-15	-5	5	15	25	Сумма
ni	19	42	71	56	12	200
xini	-285	-210	355	840	300	1000
(x x)2 n i i	7600	4200	0	5600	4800	22200

Выборочное среднее:

x ¹ _∑ xn

¹ 1000  5 .

_n i i

200

Выборочная дисперсия:

D ¹ _∑(x x)²n

¹ 22200  111 .

_n i i

200

Выборочная исправленная дисперсия:

S²  ⁿ D ²⁰⁰111  111, 558 .

n1 199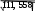

Выборочное исправленное среднее квадратическое отклонение: S  10, 562 .

Таким образом, предполагаем, что исследуемая величина имеет нормальный закон

распределения с параметрами a 5 и   10, 562 .
Построим теоретическую нормальную кривую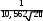

1 ^ (x a)^{2  } (x 5)^{2 }

f(x) 

exp_ 

2 <sup>2  

exp </sup> 2 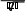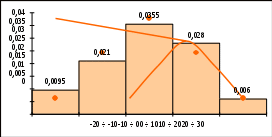10, 562^{2 }

   


и гистограмму относительных частот на одном чертеже

Расчетная таблица:

xi	-20 ÷ -10	-10 ÷ 0	0 ÷ 10	10 ÷ 20	20 ÷ 30
ni	19	42	71	56	12
pi	1,9	4,2	7,1	5,6	1,2
wi	0,095	0,21	0,355	0,28	0,06
fi	0,0095	0,021	0,0355	0,028	0,006
f(xi)	0,006289	0,024127	0,037771	0,024127	0,006289

С помощью критерия согласия Пирсона проверим, согласуется ли гипотеза с опытными данными на уровне значимости   0, 05 .

Пронормируем случайную величину X, то есть перейдем к величине

_Z x x_,

S

вычислим концы интервалов по формулам

_z x_i x_,

i _S

^zi1

_ x_i1  x_.

S

Вычислим теоретические (выравнивающие частоты) n_i'  nP_i, где n 200 ,

P_i (z_i1 )  (z_i) - вероятность попадания в интервал (z_i, z_i1 ) , (z) - функция Лапласа.

Для нахождения значений составим расчетную таблицу (первые два интервала объединили как малочисленные):

xi	xi1	ni	zi	zi1	(zi)	(zi1 )	Pi	ni'	(n n')2 i i ni'
-20	-10	19		-1,42	-0,5	-0,4222	0,0778	15,56	0,761
-10	0	42	-1,42	-0,47	-0,4222	-0,1808	0,2414	48,28	0,817
0	10	71	-0,47	0,47	-0,1808	0,1808	0,3616	72,32	0,024
10	20	56	0,47	1,42	0,1808	0,4222	0,2414	48,28	1,234
20	30	12	1,42		0,4222	0,5	0,0778	15,56	0,814

Сумма 200,000 1,000 200,000 3,650
Сравним эмпирические и теоретические частоты, используя критерий Пирсона:

_{ 2  ∑} (n n')² _

i i

n_i'

3, 65 .

По таблице критических точек распределения ² по уровню значимости   0,05 и числу степеней свободы k = 5 - 3 = 2, находим ² _кр. = 6,0. Так как ² _набл. = 3,65 < ² _кр. = 6,0, то следует принять гипотезу о нормальном распределении данной величины.