Практ.раб 4.к надеж.Эмпир.. Построение кривой нормального распределения по опытным данным. Проверка гипотезы о нормальном распределении выборки

• Название: Построение кривой нормального распределения по опытным данным. Проверка гипотезы о нормальном распределении выборки
• Дата: 06.12.2021
• Размер: 378.01 Kb.
• Имя файла: Практ.раб 4.к надеж.Эмпир..docx
• Тип: Лекция; #293612
• страница: 2 из 9

Тема: Проверка гипотезы о нормальном распределении

ЗАДАНИЕ. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X по результатам выборки:
X 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,1 2,3

N 7 9 28 27 30 26 21 25 22 9 5
РЕШЕНИЕ.

Вычислим параметры выборки. Составим расчетную таблицу:

xi	ni	xini	(x  x)2 n i i
0,3	7	2,1	6,461
0,5	9	4,5	5,209
0,7	28	19,6	8,805
0,9	27	24,3	3,514
1,1	30	33	0,775
1,3	26	33,8	0,040
1,5	21	31,5	1,202
1,7	25	42,5	4,823
1,9	22	41,8	8,990
2,1	9	18,9	6,339
2,3	5	11,5	5,400
Сумма	209	263,5	51,558

Выборочное среднее:

x  ¹ _ x n

 ¹ 263, 5  1, 261.

_n ii

209

Выборочная исправленная дисперсия:

S ²  ¹ _(x  x )² n  ¹ 51, 558  0, 248 .

n1 ^{i i} 208

Выборочное исправленное среднее квадратическое отклонение:

S  0, 498 .

Выдвинем гипотезу

H₀ : распределение генеральной совокупности Xподчинено

нормальному закону с параметрами

a  1, 261 и

  0, 498 . Проверим эту гипотезу по

критерию Пирсона при уровне значимости   0, 05 .


i
Рассчитываем теоретические частоты n⁰ по формуле

n⁰  ^nh (u ) , где u  ^{xi  x} , h  0, 2 – шаг между вариантами, (u) 



¹ _eu ² / 2 _.

i _S i i _S

Вычисления представим в виде таблицы:

xi	ui	 (ui )	n 0 i	ni	(n  n0 )2 i i n0 i
0,3	-1,930	0,062	5,204	7	0,620
0,5	-1,528	0,124	10,422	9	0,194
0,7	-1,126	0,212	17,762	28	5,901
0,9	-0,725	0,307	25,760	27	0,060
1,1	-0,323	0,379	31,793	30	0,101
1,3	0,079	0,398	33,390	26	1,636
1,5	0,481	0,355	29,842	21	2,620
1,7	0,882	0,270	22,697	25	0,234
1,9	1,284	0,175	14,689	22	3,638
2,1	1,686	0,096	8,090	9	0,102
2,3	2,087	0,045	3,792	5	0,385
Сумма					15,491

₂ ¹¹ (n  n⁰ )²

Наблюдаемое значение критерия вычислим по формуле

_набл  _^{i i}  15, 491.

n
0



i1 _i

По таблице критических значений

² при уровне значимости   0, 05

и числе степеней

кр
свободы

k l 3  11 3  8

найдем

 ²  15, 507 . Так как  ²  15, 491   ²

 15, 507 ,

кр набл кр

нулевую гипотезу о нормальном распределении можно принять при данном уровне значимости.

Проверка гипотезы о нормальности распределения

ЗАДАНИЕ.

Были исследованы 200 готовых деталей на отклонения истинного размера от расчетного. Сгруппированные данные приведены в следующей таблице:

Границы интервалов в микронах	-20 ÷ -10	-10 ÷ 0	0 ÷ 10	10 ÷ 20	20 ÷ 30
Число деталей с данной величиной отклонения	19	42	71	56	12

По данному статистическому ряду построить гистограмму. По виду гистограммы выдвинуть гипотезу о виде закона распределения (например, предположить, что исследуемая величина имеет нормальный закон распределения). Подобрать параметры закона распределения (равные их оценкам на основе опытных данных). На том же графике построить функцию плотности вероятности, соответствующую выдвинутой гипотезе. С помощью критерия согласия проверить, согласуется ли гипотеза с опытными данными. Уровень значимости взять, например, равным 0,05.

РЕШЕНИЕ. Построим гистограмму частот, для чего дополнительно вычислим плотность

частот

p ⁿⁱi <sub>h

</sub> n_i

10

. Получаем:

xi	-20 ÷ -10	-10 ÷ 0	0 ÷ 10	10 ÷ 20	20 ÷ 30
ni	19	42	71	56	12
pi	1,9	4,2	7,1	5,6	1,2

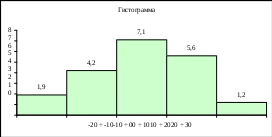По виду гистограммы можно предположить, что исследуемая величина имеет нормальный закон распределения.
Найдем точечные оценки параметров распределения. Для этого перейдем к простому вариационному ряду, выбирая в качестве вариант середины интервалов, составим расчетную таблицу:

xi	-15	-5	5	15	25	Сумма
ni	19	42	71	56	12	200
xini	-285	-210	355	840	300	1000
(x x)2 n i i	7600	4200	0	5600	4800	22200

Выборочное среднее:

x ¹ _∑ xn

¹ 1000  5 .

_n i i

200

Выборочная дисперсия:

D ¹ _∑(x x)²n

¹ 22200  111 .

_n i i

200

Выборочная исправленная дисперсия:

S²  ⁿ D ²⁰⁰111  111, 558 .

n1 199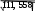

Выборочное исправленное среднее квадратическое отклонение: S  10, 562 .

Таким образом, предполагаем, что исследуемая величина имеет нормальный закон

распределения с параметрами a 5 и   10, 562 .
Построим теоретическую нормальную кривую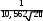

1 ^ (x a)^{2  } (x 5)^{2 }

f(x) 

exp_ 

2 <sup>2  

exp </sup> 2 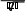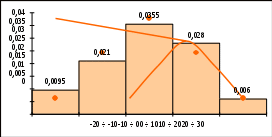10, 562^{2 }

   


и гистограмму относительных частот на одном чертеже

Расчетная таблица:

xi	-20 ÷ -10	-10 ÷ 0	0 ÷ 10	10 ÷ 20	20 ÷ 30
ni	19	42	71	56	12
pi	1,9	4,2	7,1	5,6	1,2
wi	0,095	0,21	0,355	0,28	0,06
fi	0,0095	0,021	0,0355	0,028	0,006
f(xi)	0,006289	0,024127	0,037771	0,024127	0,006289

С помощью критерия согласия Пирсона проверим, согласуется ли гипотеза с опытными данными на уровне значимости   0, 05 .

Пронормируем случайную величину X, то есть перейдем к величине

_Z x x_,

S

вычислим концы интервалов по формулам

_z x_i x_,

i _S

^zi1

_ x_i1  x_.

S

Вычислим теоретические (выравнивающие частоты) n_i'  nP_i, где n 200 ,

P_i (z_i1 )  (z_i) - вероятность попадания в интервал (z_i, z_i1 ) , (z) - функция Лапласа.

Для нахождения значений составим расчетную таблицу (первые два интервала объединили как малочисленные):

xi	xi1	ni	zi	zi1	(zi)	(zi1 )	Pi	ni'	(n n')2 i i ni'
-20	-10	19		-1,42	-0,5	-0,4222	0,0778	15,56	0,761
-10	0	42	-1,42	-0,47	-0,4222	-0,1808	0,2414	48,28	0,817
0	10	71	-0,47	0,47	-0,1808	0,1808	0,3616	72,32	0,024
10	20	56	0,47	1,42	0,1808	0,4222	0,2414	48,28	1,234
20	30	12	1,42		0,4222	0,5	0,0778	15,56	0,814

Сумма 200,000 1,000 200,000 3,650
Сравним эмпирические и теоретические частоты, используя критерий Пирсона:

_{ 2  ∑} (n n')² _

i i

n_i'

3, 65 .

По таблице критических точек распределения ² по уровню значимости   0,05 и числу степеней свободы k = 5 - 3 = 2, находим ² _кр. = 6,0. Так как ² _набл. = 3,65 < ² _кр. = 6,0, то следует принять гипотезу о нормальном распределении данной величины.