Практ.раб 4.к надеж.Эмпир.. Построение кривой нормального распределения по опытным данным. Проверка гипотезы о нормальном распределении выборки

• Название: Построение кривой нормального распределения по опытным данным. Проверка гипотезы о нормальном распределении выборки
• Дата: 06.12.2021
• Размер: 378.01 Kb.
• Имя файла: Практ.раб 4.к надеж.Эмпир..docx
• Тип: Лекция; #293612
• страница: 8 из 9

Проверка гипотезы по критерию Колмогорова-Смирнова

ЗАДАНИЕ.

В течение месяца выборочно осуществлялась проверка торговых точек города по продаже овощей. Результаты двух проверок по недовесам покупателям одного вида овощей приведены в таблице:



Можно ли считать при уровне значимости 0,05, что недовесы овощей являются устойчивым и закономерным процессом при продаже овощей в данном городе (т.е. описываются одной и той же функцией распределения)?

РЕШЕНИЕ.

Используем критерий Колмогорова-Смирнова (проверяем гипотезу

^{H0 : F1}  ^x ^{ F2}  ^x ^{- о}

том, что данные описываются одной и той же функцией распределения). Вычислим накопленные частоты для обоих выборок и значения эмпирических функций (относительные накопленные частоты). Расчеты будем вести в таблице.

интер- вал	n1	n2	níàê 1	níàê 2	* níàê F1  x 1 n1	* níàê F2  x 2 n2	F*  x  F*  x 1 2
1	3	5	3	5	0,027	0,050	0,023
2	10	12	13	17	0,118	0,170	0,052
3	15	8	28	25	0,255	0,250	0,005
4	20	25	48	50	0,436	0,500	0,064
5	12	10	60	60	0,545	0,600	0,055
6	5	8	65	68	0,591	0,680	0,089
7	25	20	90	88	0,818	0,880	0,062
8	15	7	105	95	0,955	0,950	0,005
9	5	5	110	100	1,000	1,000	0,000

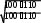Найдем наибольшее отклонение, затем вычисляем значение критерия:

^{  max F*}  ^x ^{ F*}  ^x ^{  0, 089   0, 644 .}

_xi 1 2

Так как

  _0,05  1, 36 , то гипотеза принимается, можно считать, что недовесы овощей

описываются одной и той же функцией распределения.

Проверка гипотезы по критерию Вилкоксона

ЗАДАНИЕ.

Имеется выборка прибыли коммерческой фирмы за 14 недель до (х_i) и после (y_i)проведения новой экономической политики. На уровне значимости α = 0,05 по критерию Вилкоксона проверить гипотезу о том, что введение новой экономической политики в среднем привело к увеличению производительности.

Вар.№		Выборка
8	х	52	51	48	52	54	50	51	51	52	52	53	56	51	50
	y	44	47	57	54	39	65	46	51	58	46	62	52	65	47

РЕШЕНИЕ.

Вычислим разности наблюдений, абсолютные значения разностей и ранги последних значений. Результаты занесем в таблицу:

x	y	y x	y x	ранг
52	44	-8	8	9
51	47	-4	4	4,5
48	57	9	9	10,5
52	54	2	2	2
54	39	-15	15	13,5
50	65	15	15	13,5
51	46	-5	5	6
51	51	0	0	1
52	58	6	6	7,5
52	46	-6	6	7,5
53	62	9	9	10,5
56	52	-4	4	4,5
51	65	14	14	12
50	47	-3	3	3

Найдем эмпирическое значение критерия (сумму рангов для тех наблюдений, где была замечена неправильная тенденция, в данном случае уменьшение производительности, эти значения выделены жирным в таблице).

Получаем T_эмп 4, 5 13, 5  6  7, 5  4, 5  3  39 .

Найдем критическое значение критерия для уровня значимости

  0, 05

и числу

кр
наблюдений n 14 из таблицы, T 25 .

Так как эмпирическое значение больше критического, нельзя утверждать, что производительность увеличилась.

Проверка гипотезы по критерию  ²

ЗАДАНИЕ.

Используя критерий «хи-квадрат» при уровне значимости α = 0,05, проверить, существует ли зависимость уровня интеллектуального развития учеников от типа школы по результатам обследования 100 сельских и 100 городских школьников:

Тип школы	Уровень интеллектуального развития
	низкий	нормальный	высокий
Городская	25	50	25
Сельская	52	41	7