Практ.раб 4.к надеж.Эмпир.. Построение кривой нормального распределения по опытным данным. Проверка гипотезы о нормальном распределении выборки

• Название: Построение кривой нормального распределения по опытным данным. Проверка гипотезы о нормальном распределении выборки
• Дата: 06.12.2021
• Размер: 378.01 Kb.
• Имя файла: Практ.раб 4.к надеж.Эмпир..docx
• Тип: Лекция; #293612
• страница: 4 из 9

Проверка гипотезы о распределения по равномерному закону

ЗАДАНИЕ.

В некоторой местности в течение 300 суток регистрировалась среднесуточная температура воздуха. В итоге наблюдений было получено эмпирическое распределение, приведенное в таблице 40 (в первом столбце указан интервал температуры в градусах, во втором столбце – частота n_i, т.е. количество дней, среднесуточная температура которых принадлежит этому интервалу).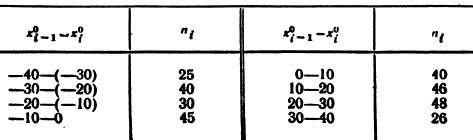



Требуется при уровне значимости 0,05 проверить гипотезу о том, что среднесуточная температура воздуха распределена равномерно.

РЕШЕНИЕ.

Перейдем к простому вариационному ряду, выбрав в качестве вариант середины интервалов.

xi	ni
-35	25
-25	40
-15	30
-5	45
5	40
15	46
25	48
35	26

Вычислим основные числовые характеристики выборки. Выборочная средняя:

x ¹ _∑ xn

¹ 450  1, 5

_n i i

300

Найдем выборочную дисперсию:

D ¹ _∑(x x)² n

¹ 136025  453, 417 .

B _n i i

300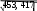

Найдем выборочное среднеквадратичное отклонение  _B  21, 294 .
Вычисления проиллюстрированы в таблице ниже:

xi	ni	xini	(x x)2 n i i
-35	25	-875	33306,25
-25	40	-1000	28090

-15	30	-450	8167,5
-5	45	-225	1901,25
5	40	200	490
15	46	690	8383,5
25	48	1200	26508
35	26	910	29178,5
Сумма	300	450	136025

Оценим параметры распределения по формулам:

a*  x

b*  x

3 _B 1, 5 

3 _B 1, 5 

3  21, 294  35, 382 ,

3  21, 294  38, 382 .

Найдем предполагаемую плотность распределения:

f(x)  ¹  ¹  ¹ .

^{b* a* 38, 382 } ^{35, 382} ^{73, 763}

Найдем теоретические частоты по формулам:

^{n'  n 1}  <sup>x

 a</sup> ^{, n'  n 1}  ^x

• 
  ^x ^{, n}
  

'  n

¹ ^{b x} ^,

¹ 73, 763 <sup>1

i</sup>73, 763

i1 i s

73, 763 ^s

занесем их в таблицу и сравним с эмпирическими частотами по критерию Пирсона.

xi	xi1	ni'	ni	(n n')2 i i ni'
-40	-30	25	21,887	0,443
-30	-20	40	40,671	0,011
-20	-10	30	40,671	2,800
-10	0	45	40,671	0,461
0	10	40	40,671	0,011
10	20	46	40,671	0,698
20	30	48	40,671	1,321
30	40	26	34,088	1,919
Сумма		300,000	300,000	7,664

Сравним эмпирические и теоретические частоты, используя критерий Пирсона:

_{ 2  ∑} (n n')² _

i i

n_i'

7, 664 .

По таблице критических точек распределения ² по уровню значимости   0, 05

степеней свободы k s 3  5 , находим ² _кр. = 11,1.

Так как ² _набл. = 7,664 < ² _кр. = 11,1, то можно принять гипотезу о равномерном распределении температуры. Данные наблюдения согласуются с гипотезой.

Проверка гипотезы по критерию Колмогорова

ЗАДАНИЕ.

Имеются выборочные данные о числе сделок, заключенных фирмой с частными лицами в течение месяца:

- число заключенных сделок	0-10	10-20	20-30	30-40	40-50
- число частных лиц	23	24	11	9	3

Проверить при уровне значимости α=0,05, используя критерий согласия Колмогорова, гипотезу о нормальном законе распределения.
РЕШЕНИЕ.

Найдем точечные оценки параметров распределения. Для этого перейдем к простому вариационному ряду, выбирая в качестве вариант середины интервалов, составим расчетную таблицу:

xi	5	15	25	35	45	Сумма
ni	23	24	11	9	3	70
xn i i	115	360	275	315	135	1200
(x x)2 n i i	3391,327	110,204	679,082	2869,898	2328,061	9378,571

Выборочное среднее:

x ¹ _∑ xn¹1200  17,143 .

_{n ii70}

Выборочная исправленная дисперсия:

S² ¹ _∑(x x)²n¹ 9378, 571  135, 921 .

n1 ⁱⁱ69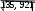

Выборочное исправленное среднее квадратическое отклонение: S  11, 659 .

Предполагаем, что исследуемая величина имеет нормальный закон распределения с

параметрами a 17,143 и   11, 659 . С помощью критерия Колмогорова проверим,

согласуется ли гипотеза с опытными данными на уровне значимости   0, 05 .

Вычислим теоретические значения функции распределения

^x1 ^

(t17,143)<sup>2 

1</sup>  ^x17,143 

F*(x)  _∫

exp_ 

_ dt   _{ } ,  - функция Лапласа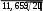

 ^

2 135, 921 _

2 _ 11, 659 _

(значения берем из таблиц).

Найдем наибольшее отклонение, затем вычисляем значение критерия:

  max F(x_i)  F *(x_i)   0, 075   0, 627 .

x_i

F*(xi)	F(xi)	F(xi)  F*(xi)
0,270	0,3286	0,059