Сущность факторного анализа
Пусть для каждого конкретного объекта измерены четыре характеристики, которые обусловлены действием двух факторов 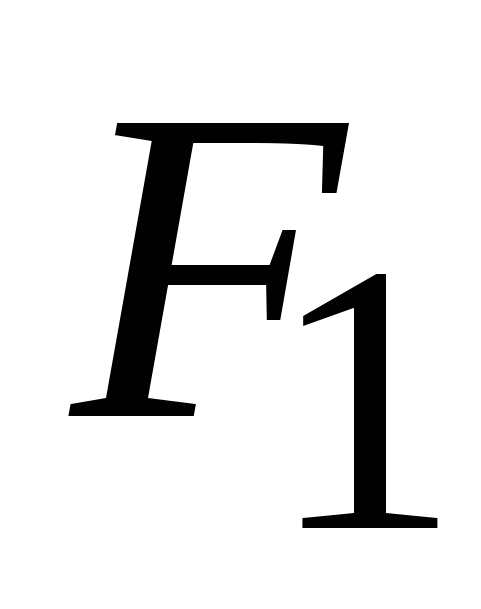 и и  . Фактор . Фактор 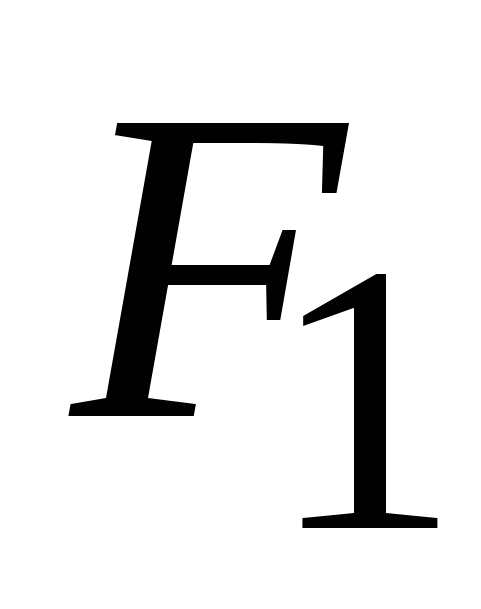 действует на все четыре характеристики объекта, а фактор действует на все четыре характеристики объекта, а фактор  действует лишь на два признака действует лишь на два признака  и и 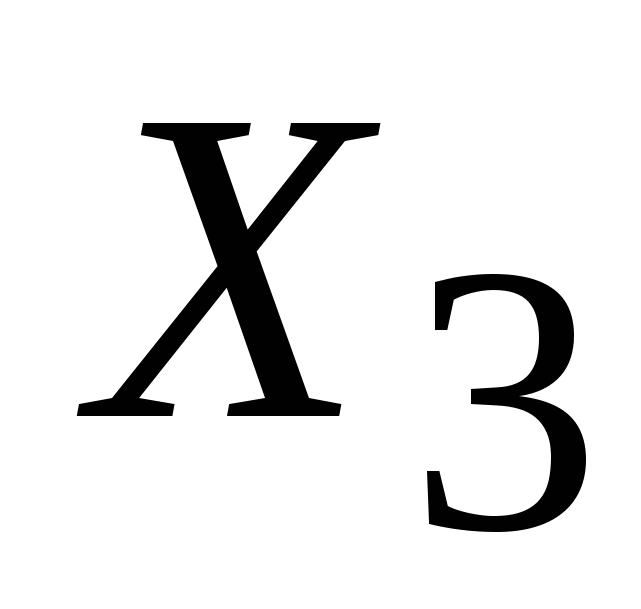 . .
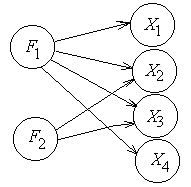
Рисунок 9.2 Схема модели факторного анализа
Значит, значения признаков  и и 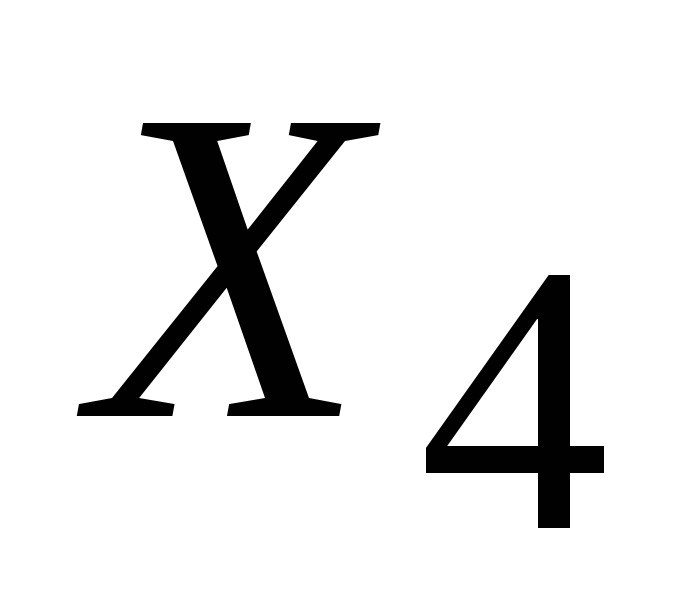 определяются только фактором определяются только фактором 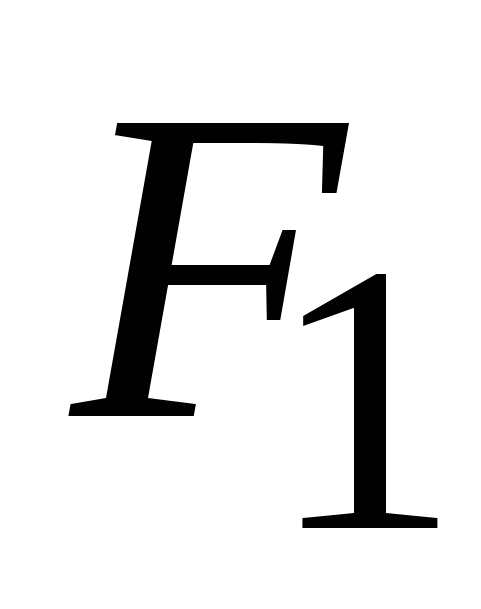 , а признаки , а признаки  и и 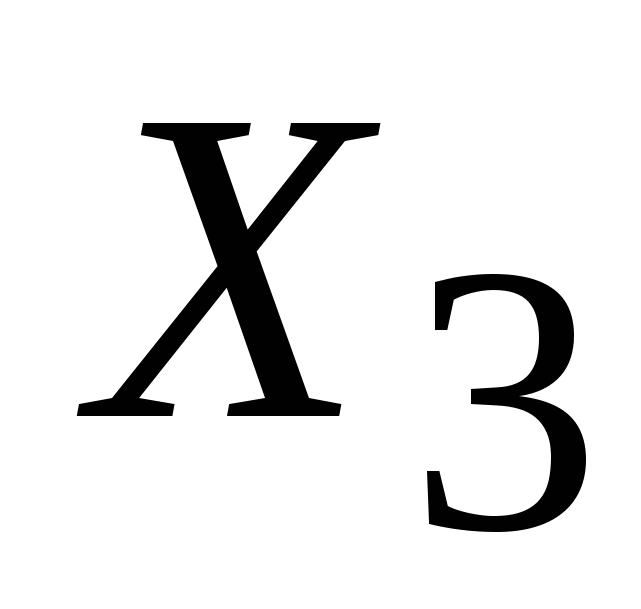 определяются совокупным действием фактором определяются совокупным действием фактором 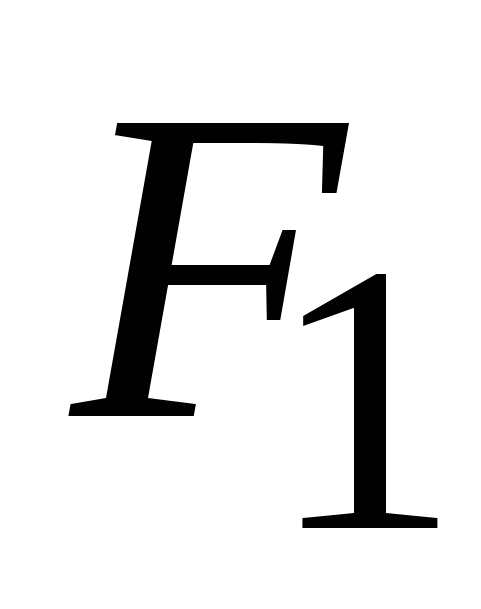 и и  . Но вначале неизвестно ни количество действующих факторов, ни их взаимосвязь с измеренными признаками. Необходимо исследовать интенсивность влияния факторов . Но вначале неизвестно ни количество действующих факторов, ни их взаимосвязь с измеренными признаками. Необходимо исследовать интенсивность влияния факторов 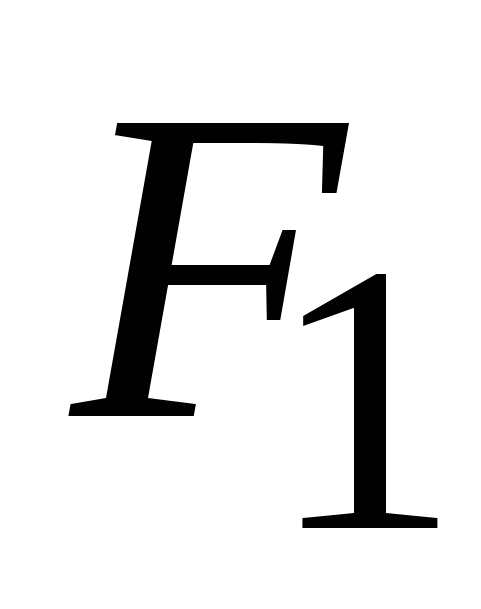 и и  на признаки на признаки  и выделить в значениях и выделить в значениях  те части, которые обусловлены действием каждого из факторов те части, которые обусловлены действием каждого из факторов 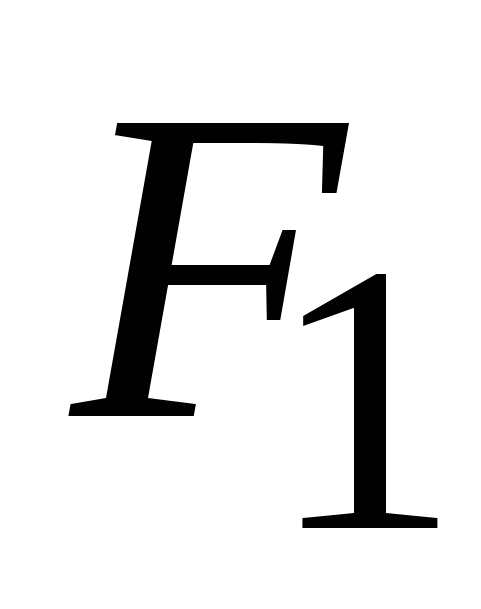 и и  в отдельности. в отдельности.
Для решения этой задачи предполагают, что  линейно зависят от линейно зависят от  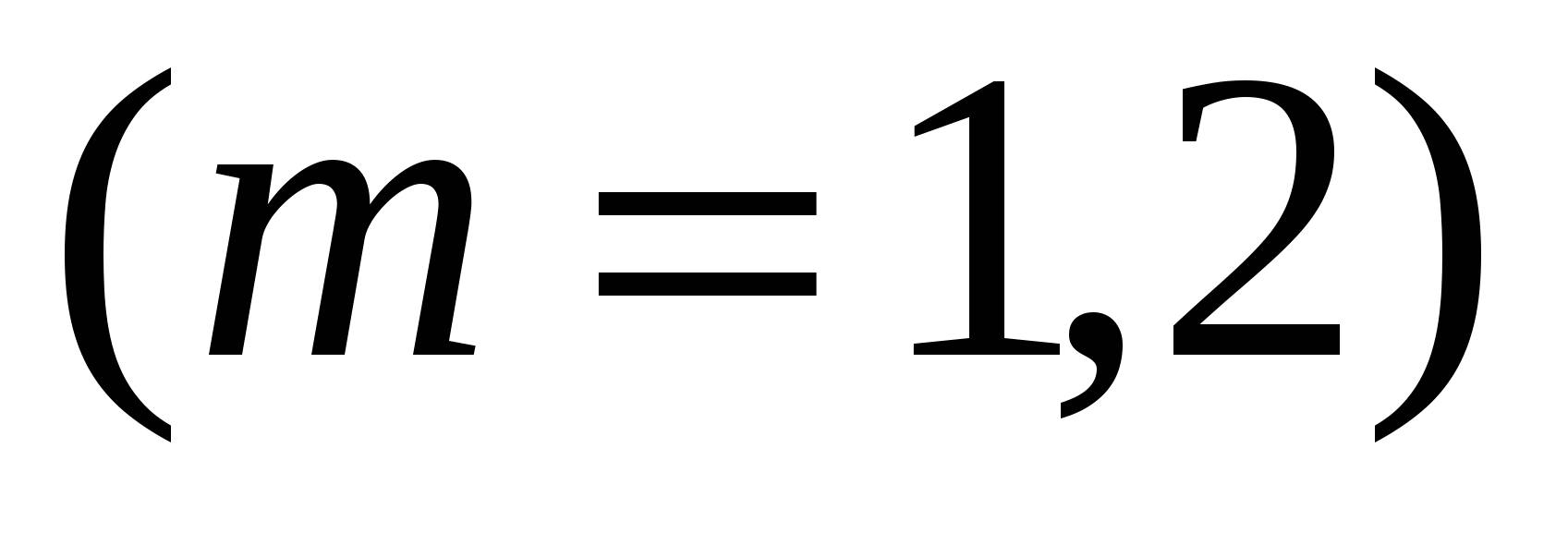 . Для рассматриваемого случая имеем . Для рассматриваемого случая имеем
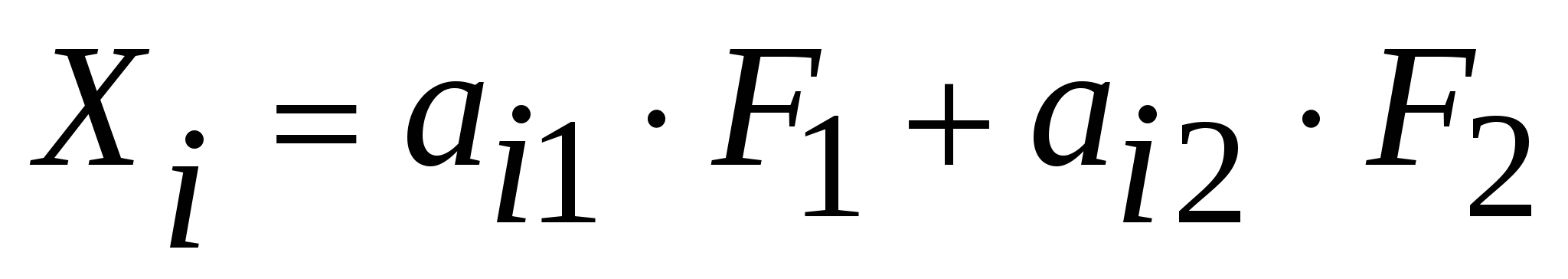 где где  (1) (1)
 - коэффициенты, называемые факторными нагрузками. - коэффициенты, называемые факторными нагрузками.
Если рассмотреть метод на основании приведенного выше примера, когда имеется  рассматриваемых объектов, для каждого из которых определено значение четырех признаков, то в четырехмерном графическом пространстве с осями координат рассматриваемых объектов, для каждого из которых определено значение четырех признаков, то в четырехмерном графическом пространстве с осями координат 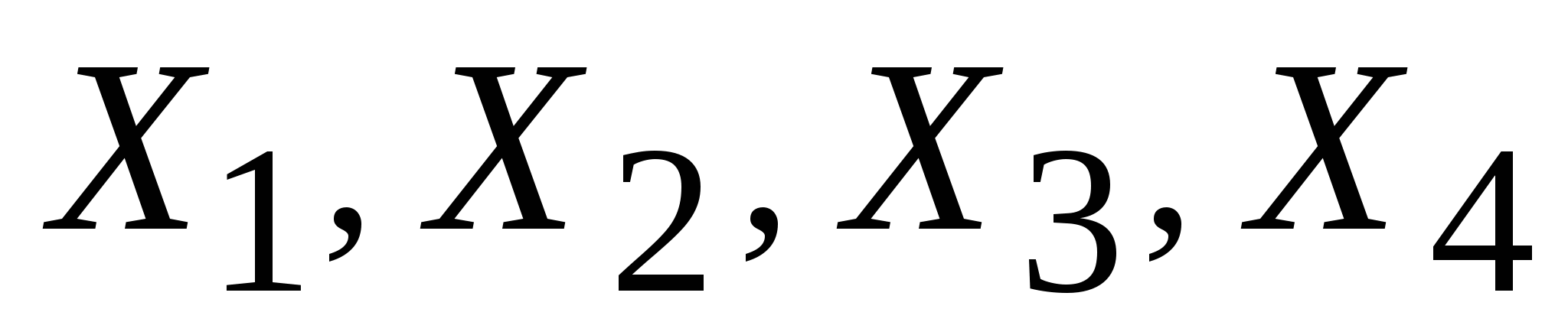 это может быть представлено как облако из это может быть представлено как облако из  точек. Для Если это четырехмерное пространство рассечь плоскостью, в которой находятся координатные оси, отвечающие признакам точек. Для Если это четырехмерное пространство рассечь плоскостью, в которой находятся координатные оси, отвечающие признакам  и и  , то в сечении мы увидим облако точек, которое в условиях взаимосвязи признаков , то в сечении мы увидим облако точек, которое в условиях взаимосвязи признаков  и и  друг с другом представляет собой эллипс рассеяния. друг с другом представляет собой эллипс рассеяния.
Перед проведением факторного анализа исходные значения признаков выборочной совокупности необходимо стандартизировать (центрировать и нормировать) с помощью преобразования
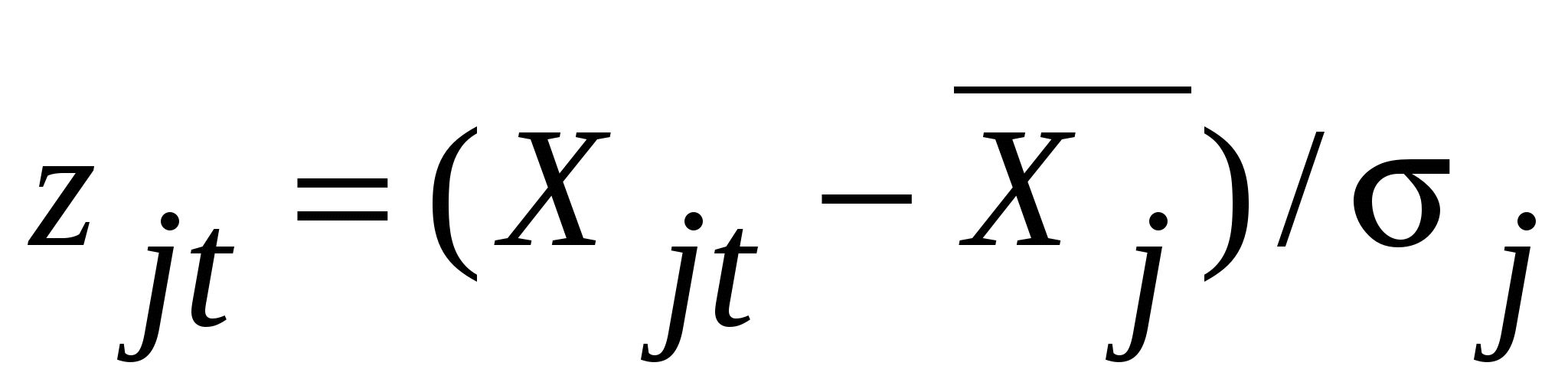
где  - исходное значение j-го признака t-того объекта; - исходное значение j-го признака t-того объекта;
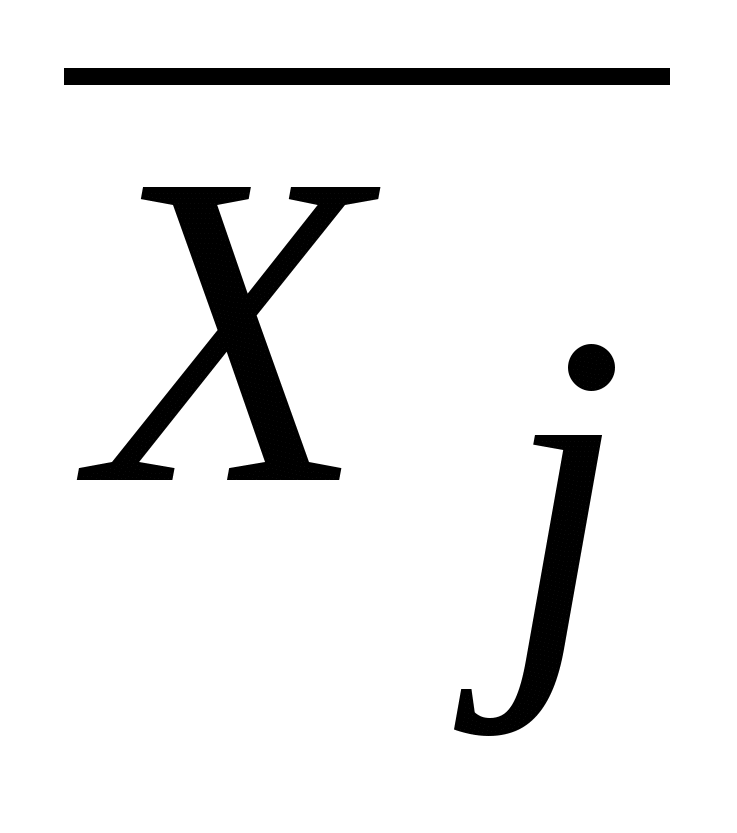 -среднее значение j-ого признака; -среднее значение j-ого признака;
 –стандартное отклонение j-ого признака. –стандартное отклонение j-ого признака.
Центр эллипса рассеяния стандартизированных значений будет находиться в точке начала координат, как показано на рисунке 9.3.

Рисунок 9.3 Эллипсы рассеянья в пространстве двух стандартизированных переменных
Форма этого эллипса (сжатость – вытянутость) будет определяться величиной коэффициента корреляции  с с  , т.е. , т.е. 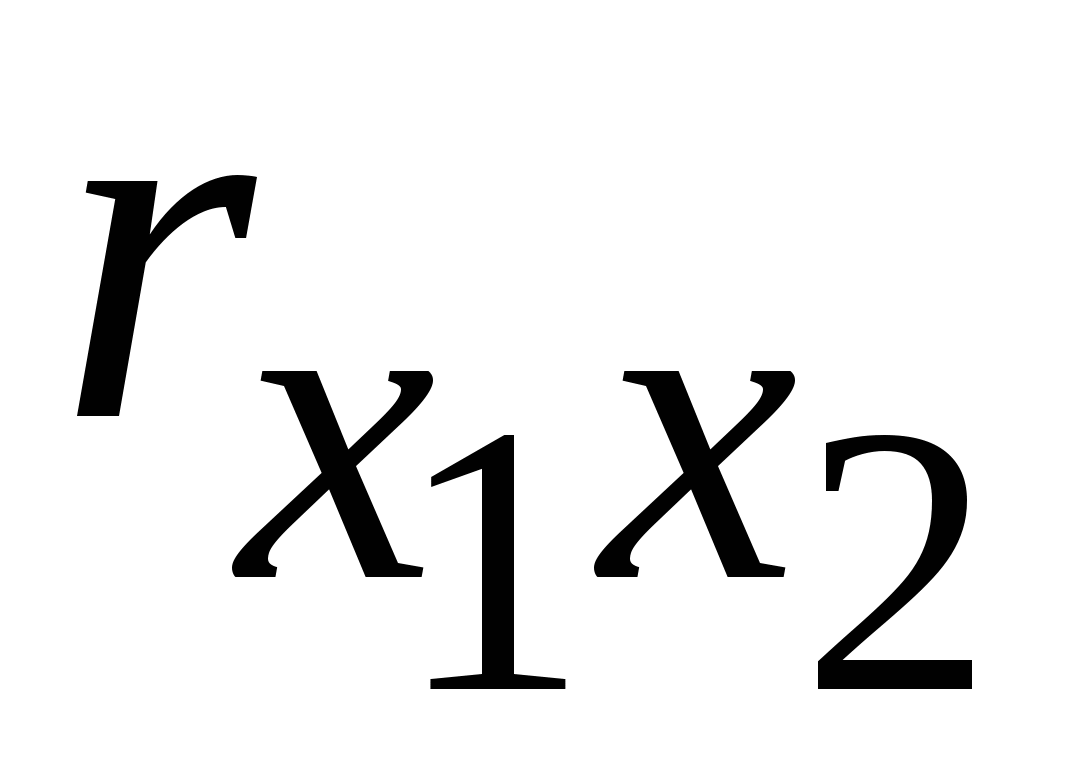 , Чем больше , Чем больше 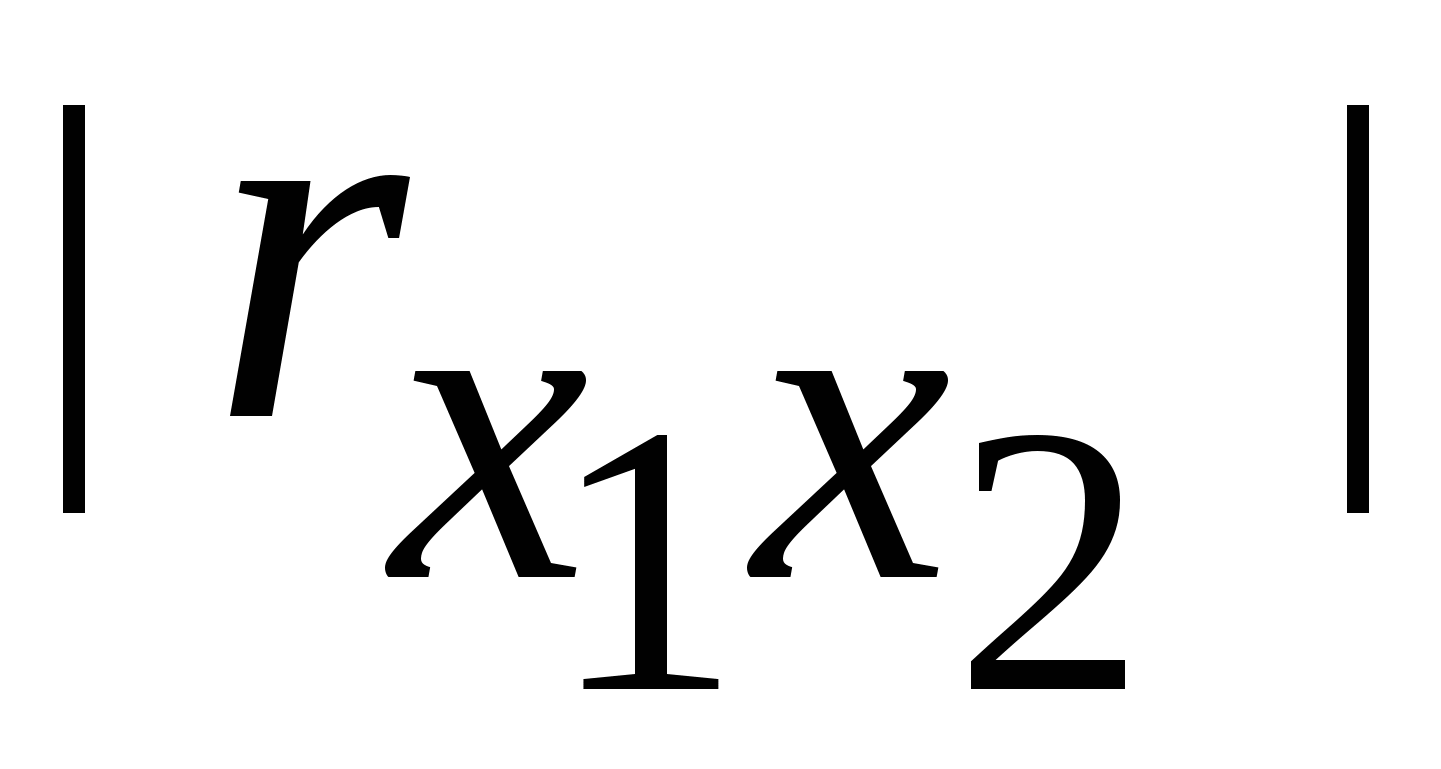 , тем более вытянут эллипс и при , тем более вытянут эллипс и при  он превращается в прямую линию, а при он превращается в прямую линию, а при 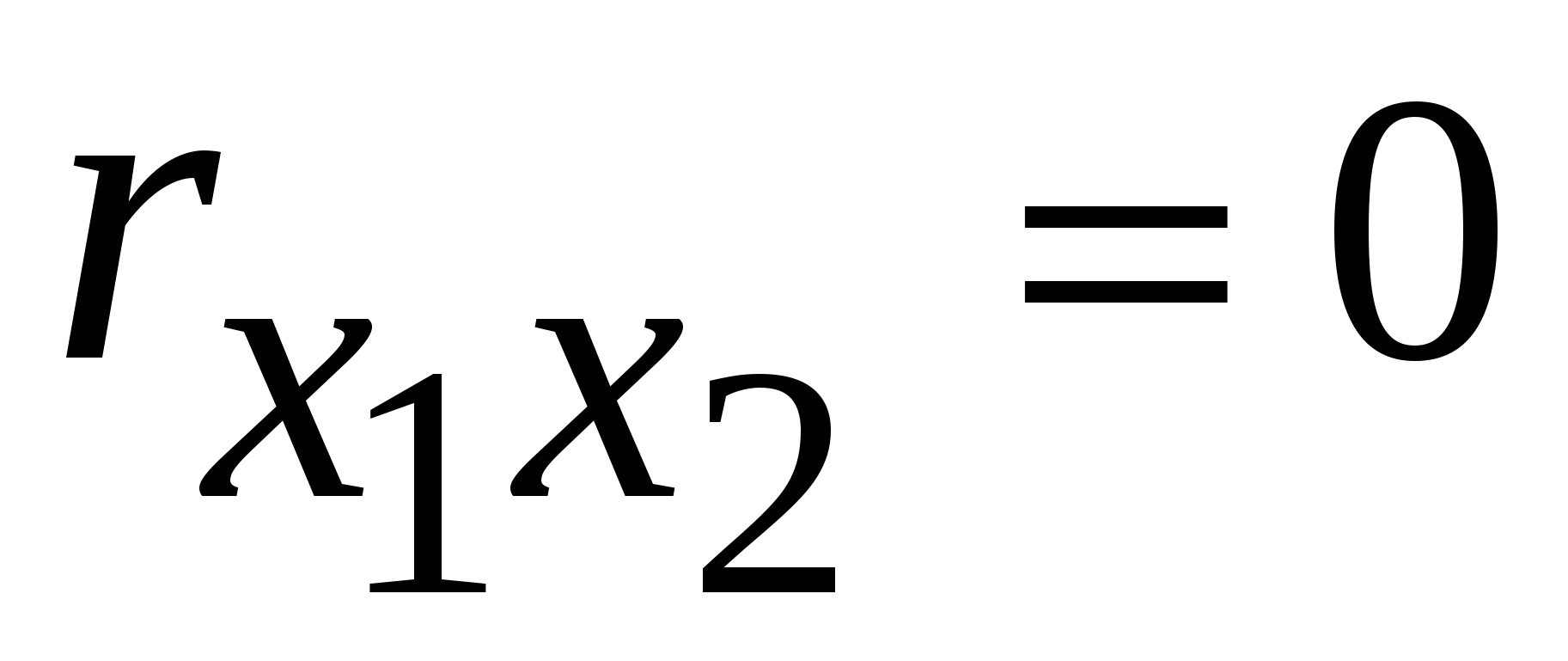 - в круг. Если провести оси эллипса - в круг. Если провести оси эллипса 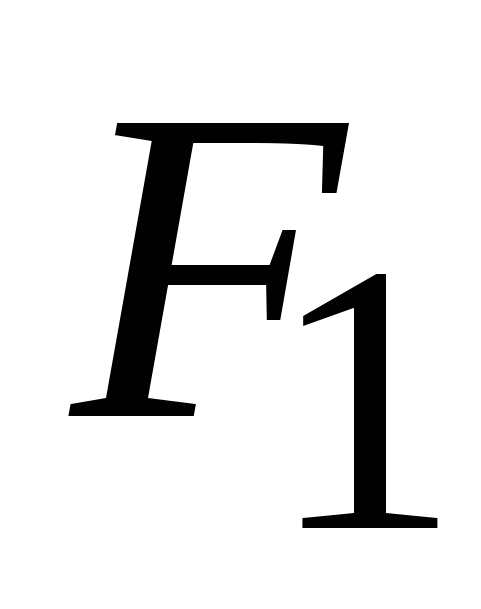 и и  , то по мере увеличения , то по мере увеличения 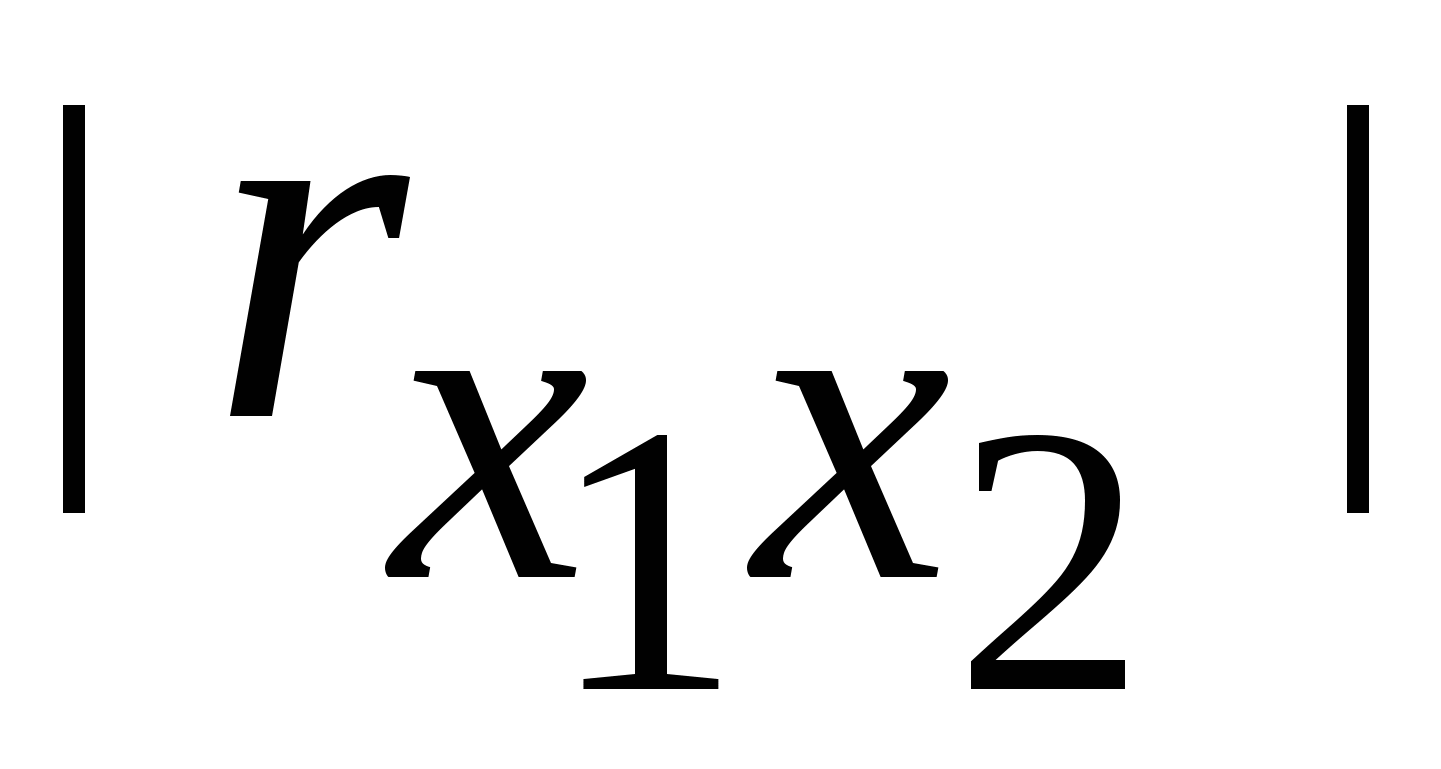 происходит уменьшение степени разброса точек наблюдений вдоль одной оси эллипса (на рисунке – ось происходит уменьшение степени разброса точек наблюдений вдоль одной оси эллипса (на рисунке – ось  ) и увеличение разброса вдоль другой оси эллипса (на рисунке – ось ) и увеличение разброса вдоль другой оси эллипса (на рисунке – ось 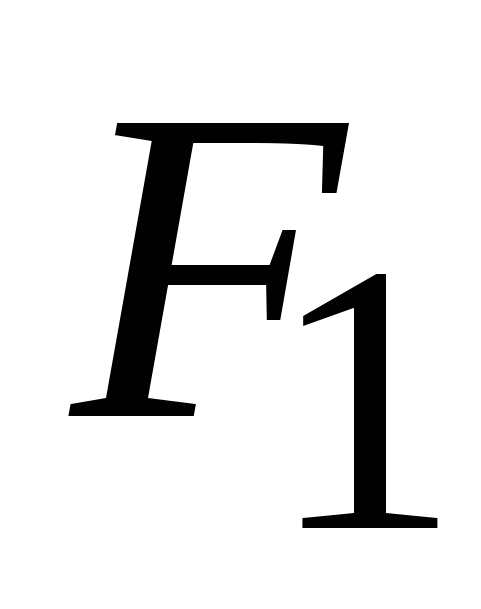 ). ).
Если перейти от исходной координатной системы  , ,  к новой к новой 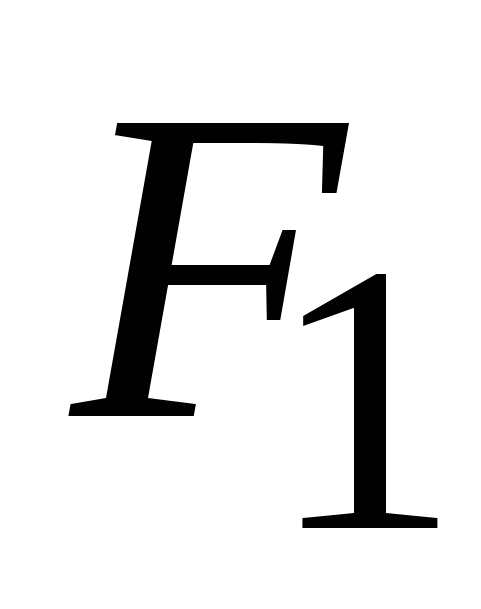 , ,  , оси которой ориентированы вдоль осей эллипса рассеяния, то, очевидно, что в новой системе координат значения переменной , оси которой ориентированы вдоль осей эллипса рассеяния, то, очевидно, что в новой системе координат значения переменной 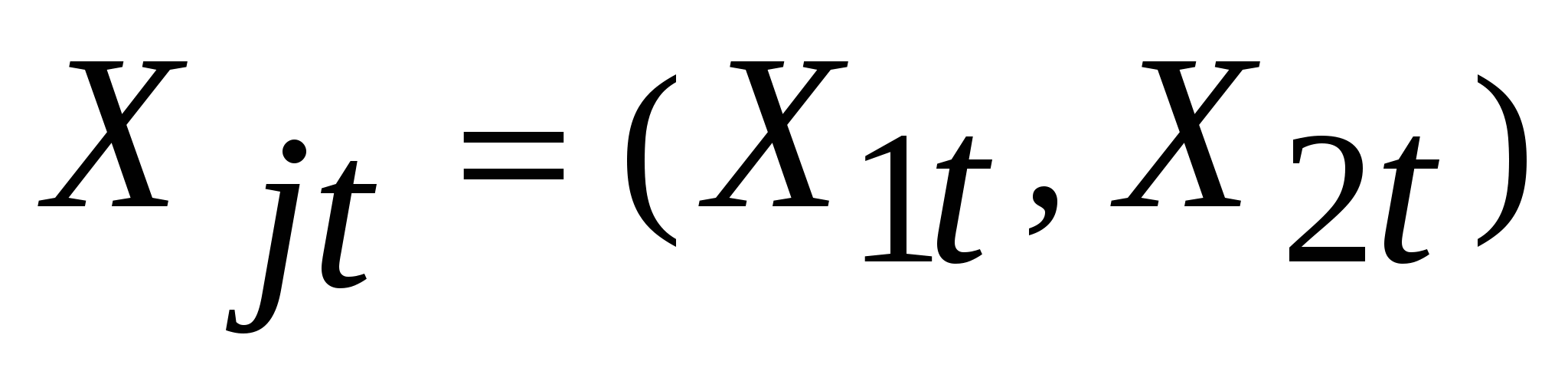 вдоль оси вдоль оси  будут иметь меньшую дисперсию, чем в исходной системе вдоль оси будут иметь меньшую дисперсию, чем в исходной системе вдоль оси  , а значения этой переменной вдоль оси , а значения этой переменной вдоль оси 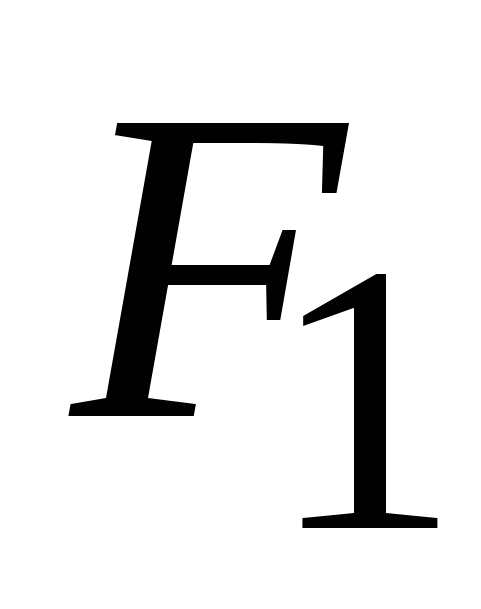 , наоборот, будут иметь большую дисперсию, чем в исходной системе вдоль оси , наоборот, будут иметь большую дисперсию, чем в исходной системе вдоль оси  . .
Поэтому переменная 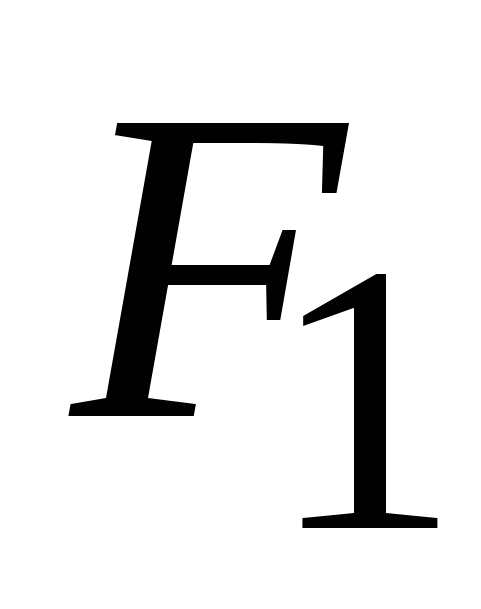 несет в себе больше информации о выборке, чем несет в себе больше информации о выборке, чем  . При этом, чем сильнее связаны между собой признаки . При этом, чем сильнее связаны между собой признаки  и и  , тем большим становится удельный вес той из новых переменных, которая ориентируется вдоль главной оси эллипса рассеяния. , тем большим становится удельный вес той из новых переменных, которая ориентируется вдоль главной оси эллипса рассеяния.
Следовательно, в случае многомерного пространства появляется возможность ранжирования переменных (признаков) по их дисперсии в соответствии с их вкладом (значимостью) в общую характеристику изучаемого объекта, т.е. по уменьшению дисперсии значений признаков вдоль новых координатных осей  . .
Трудно представить, как выглядит в многомерном пространстве облако точек выборочной многомерной совокупности. По аналогии с рассмотренным выше двумерным случаем можно предполагать, что оно представляет собой эллипсоид с несколькими разновеликими ортогональными осями. Поэтому в условиях взаимозависимости признаков для более компактного представления информации переходят к новой ортогональной системе координат (ориентированной по главным осям этого эллипсоида). Переменные этой новой системы – главные компоненты 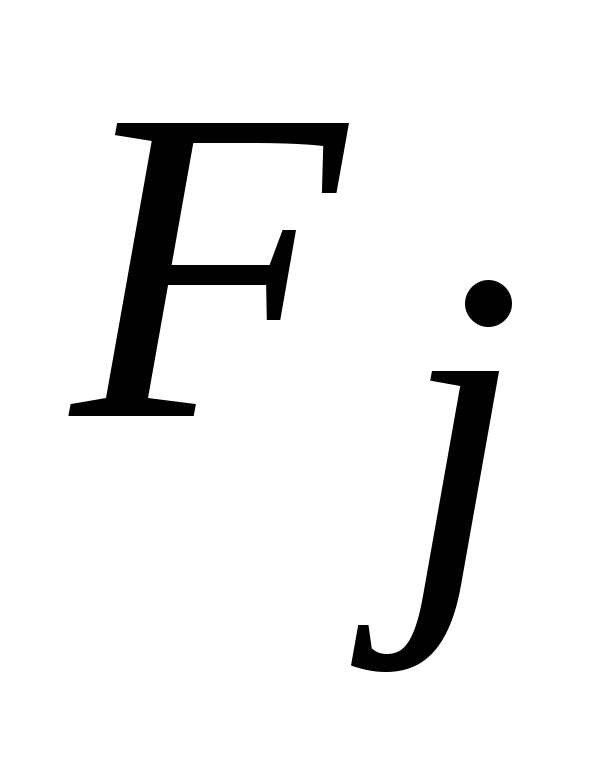 ( (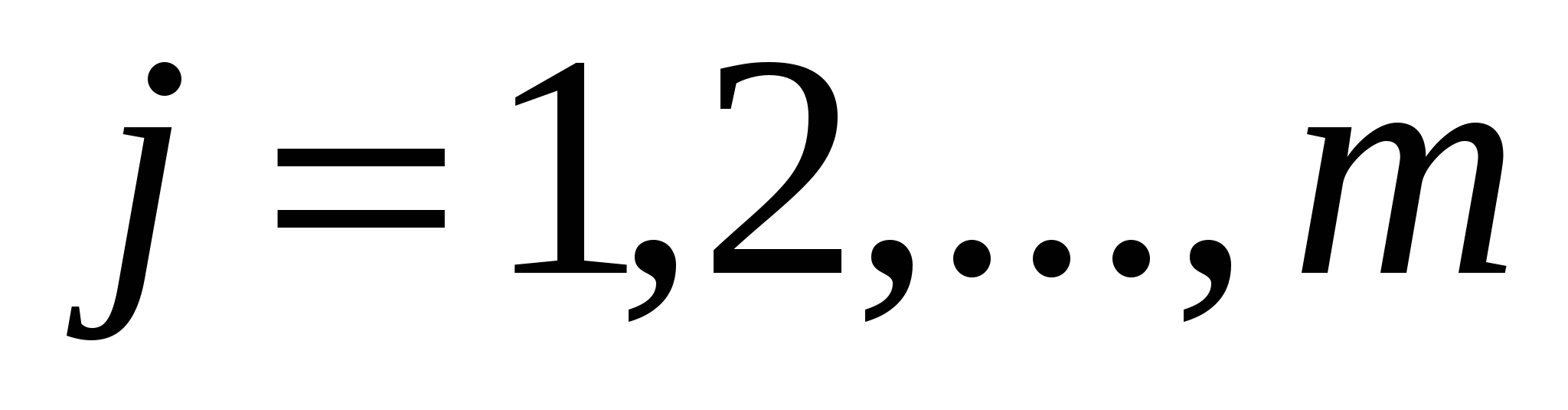 и и  ) – концентрируют в себе основную информацию об исходной выборке и снижают размерность исходного признакового пространства ( ) – концентрируют в себе основную информацию об исходной выборке и снижают размерность исходного признакового пространства ( ). Эта процедура перехода к новой системе координат ( ). Эта процедура перехода к новой системе координат (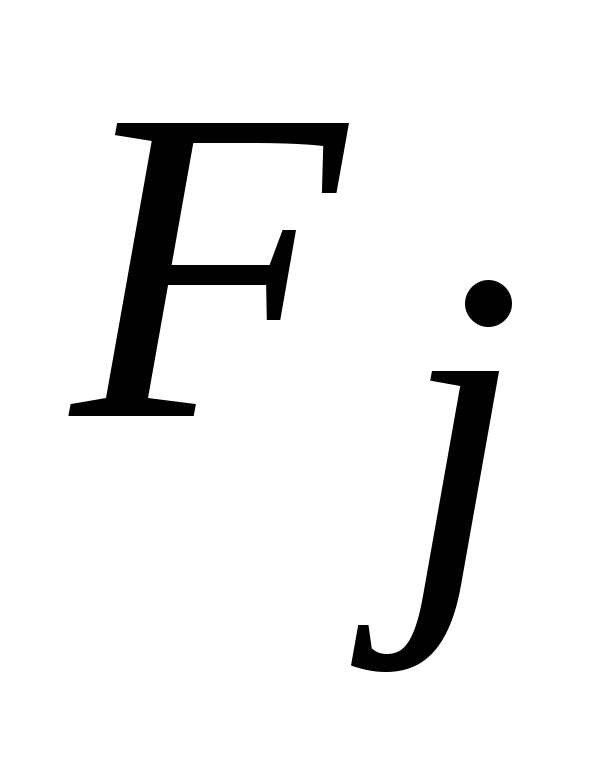 ). ).
Указанный переход не затрагивает геометрической структуры взаимного расположения точек наблюдений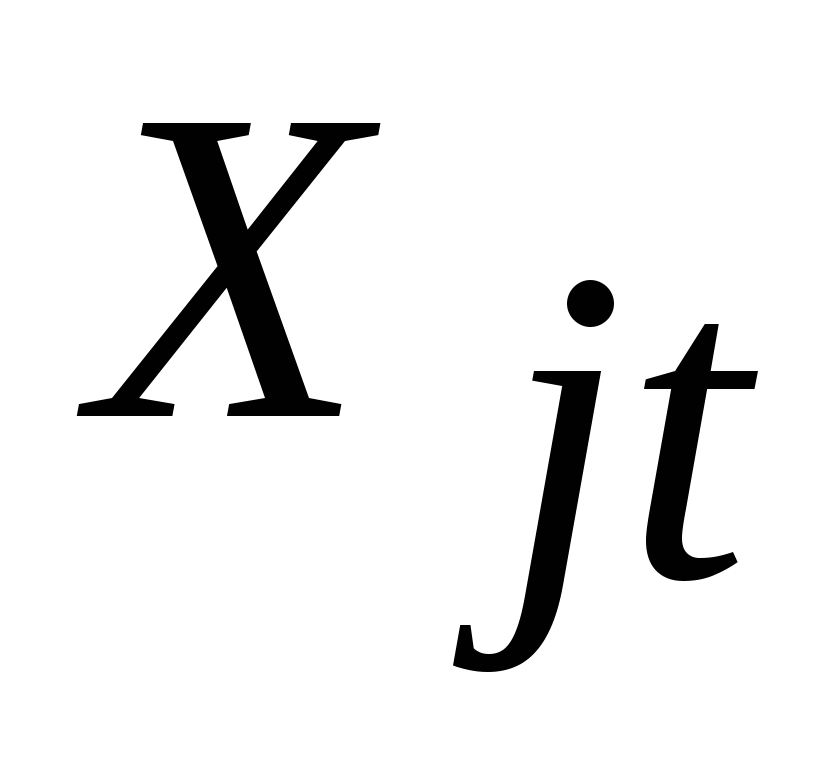 . Характер их распределения сохраняется. Поэтому суммарная дисперсия остается прежней, т.е. . Характер их распределения сохраняется. Поэтому суммарная дисперсия остается прежней, т.е.
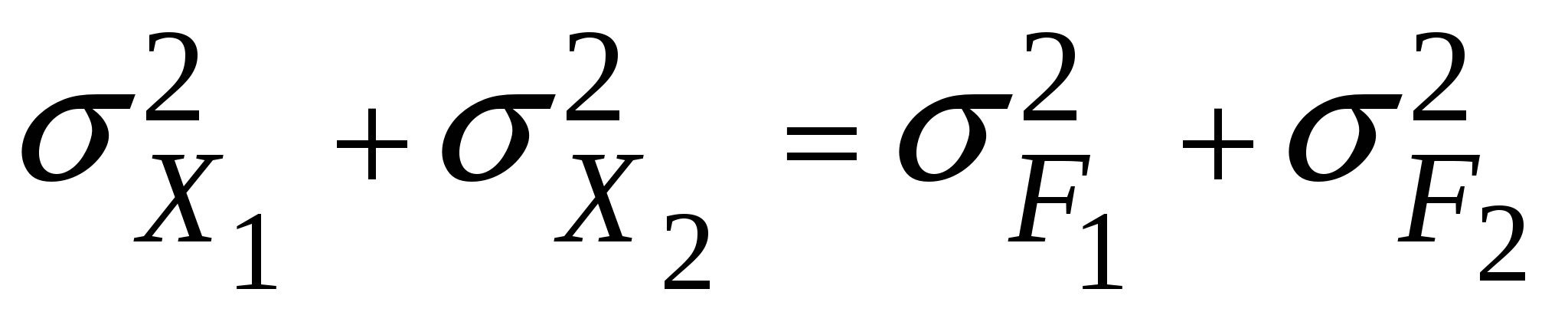 или в общем, виде или в общем, виде 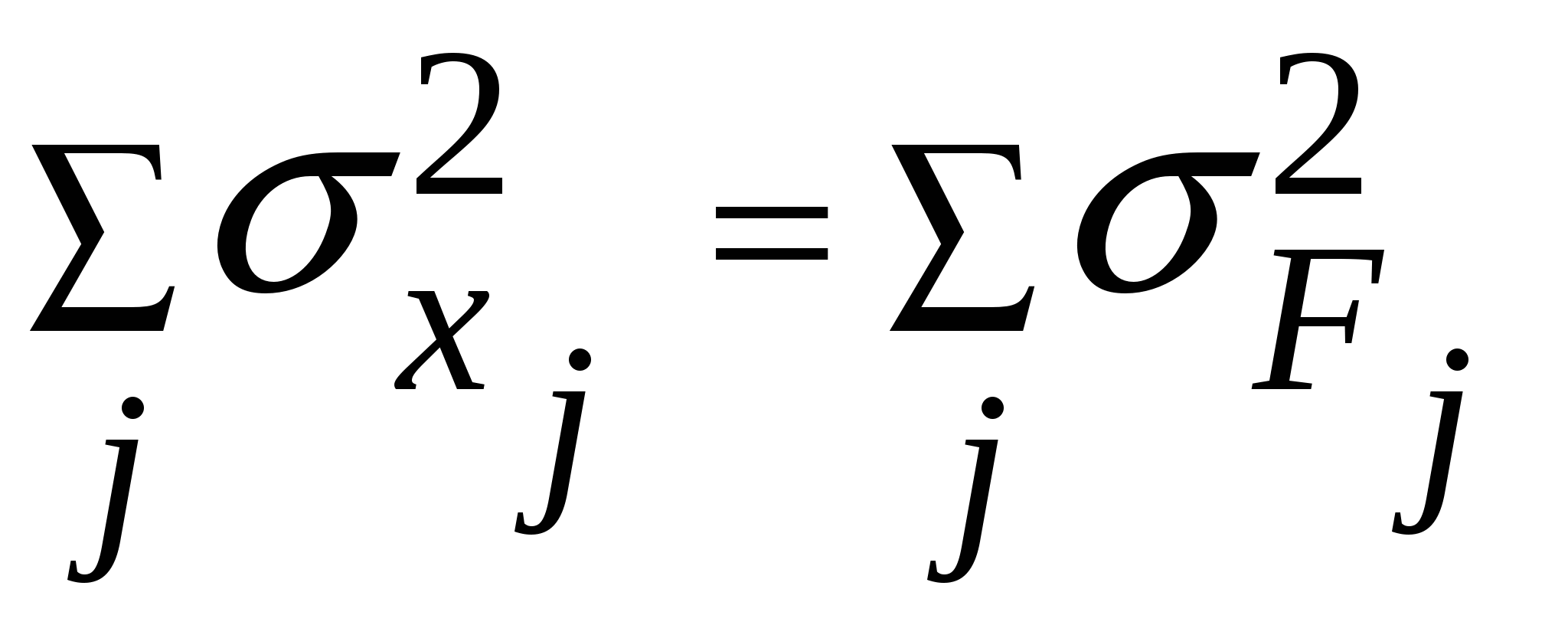
Факторные нагрузки  в уравнении в уравнении 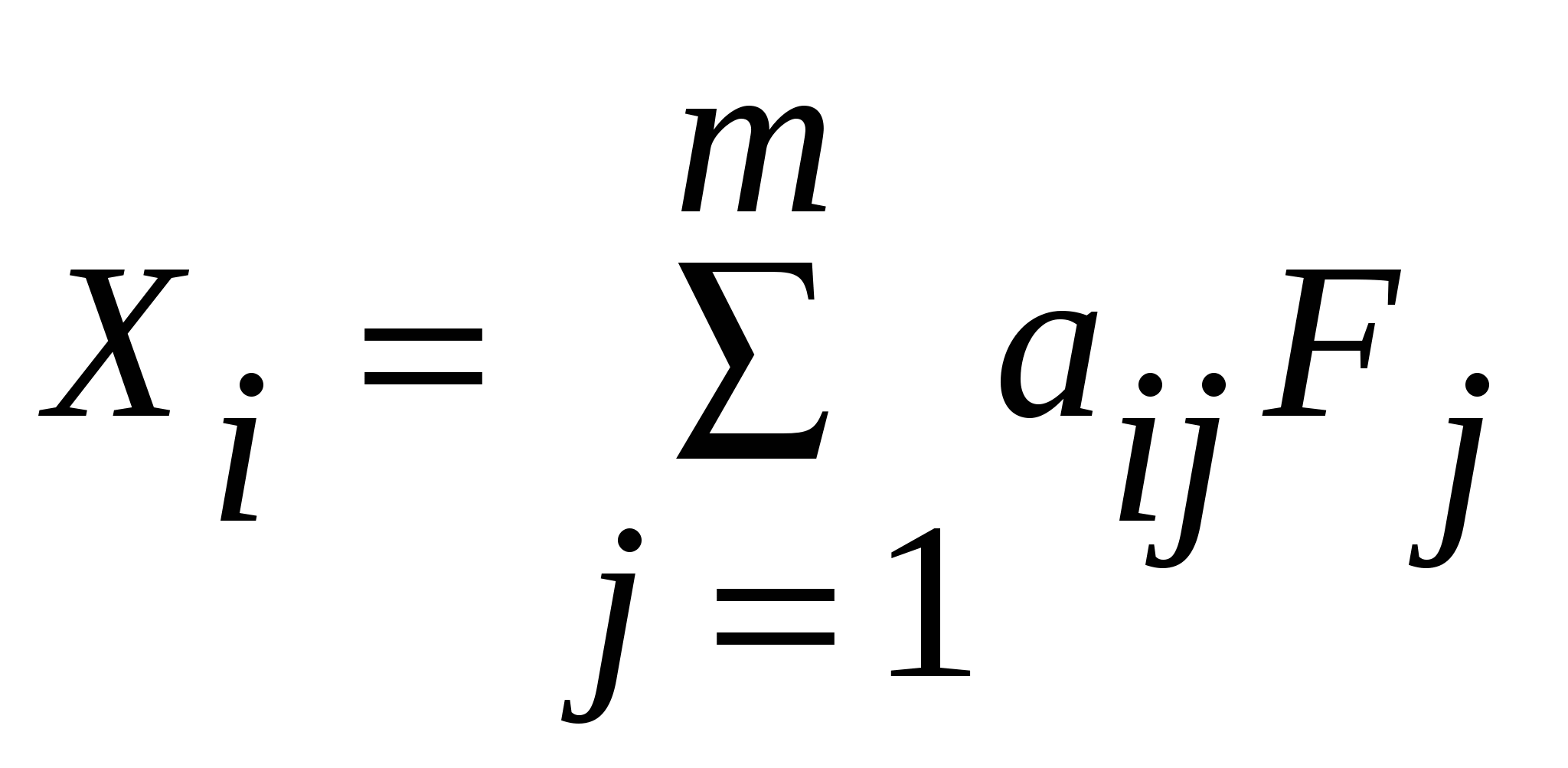 представляют собой коэффициенты корреляции между исходными представляют собой коэффициенты корреляции между исходными  и новыми и новыми 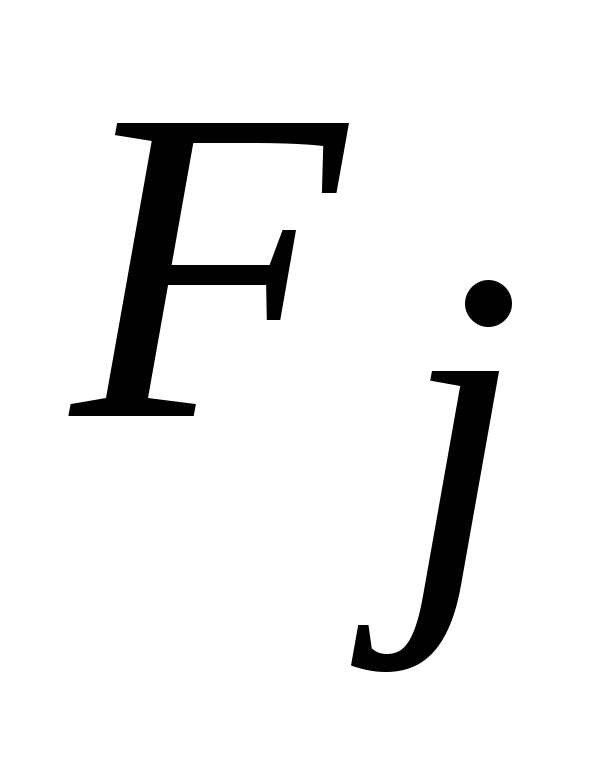 переменными переменными 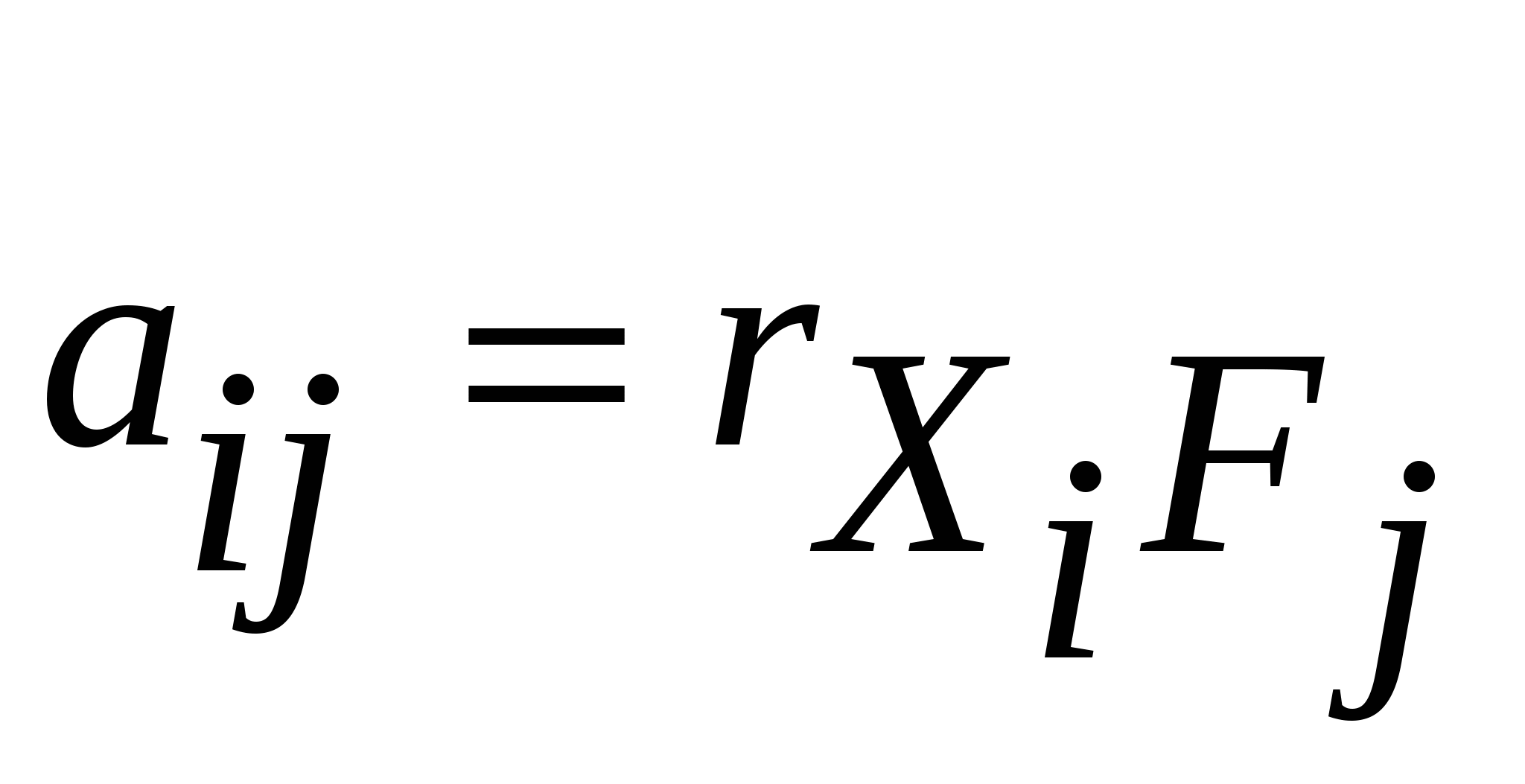 . .
|
 Скачать 0.79 Mb.
Скачать 0.79 Mb.

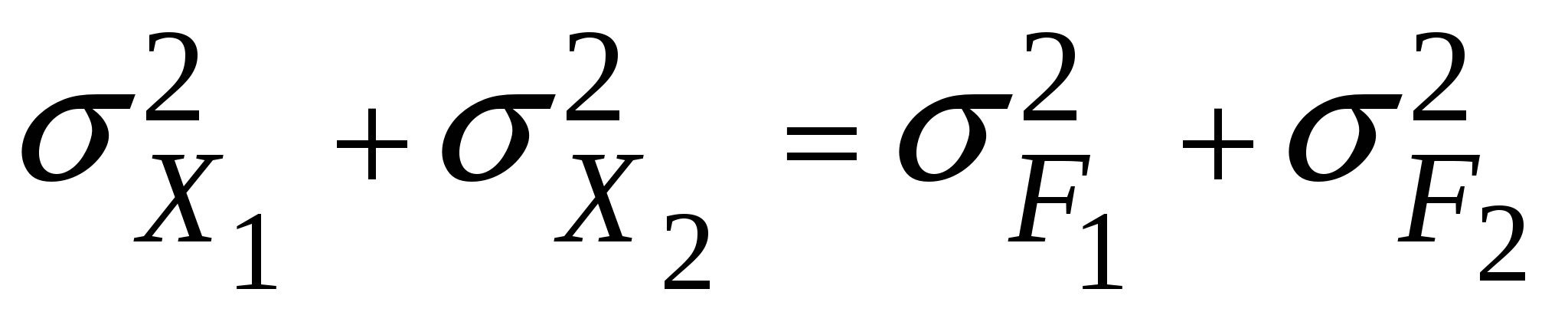 или в общем, виде
или в общем, виде 