9_факторный анализ. 9 факторный анализ
 Скачать 0.79 Mb.
|
Проблема вращения и интерпретацииЧаще всего результаты факторизации не подлежат интерпретации. Для решения вопроса о распределении переменных по факторам нужно произвести вращение факторов относительно признаков. Соотношение признаков в осях факторов при этом никак не изменятся. Сущностью факторного анализа является процедура вращения факторов, то есть перераспределения дисперсии по определённому методу. Вращение бывает ортогональным и косоугольным. Цель ортогональных вращений — определение простой структуры факторных нагрузок, целью большинства косоугольных вращений является определение простой структуры вторичных факторов, то есть косоугольное вращение следует использовать в частных случаях. Поэтому ортогональное вращение предпочтительнее. Существует более 10 методов вращения в обоих видах. Чаще других используется ортогональные методы вращения:
Из неортогональных методов вращения достаточно популярными являются:
Основное различие двух моделей факторного анализа состоит в том, что в анализе главных компонент предполагается, что должна быть использована вся изменчивость переменных, тогда как в анализе главных факторов вы используете только изменчивость переменной, общую и для других переменных. В большинстве случаев эти два метода приводят к весьма близким результатам. Однако анализ главных компонент часто более предпочтителен как метод сокращения данных, в то время как анализ главных факторов лучше применять с целью определения структуры данных.
Респондентам, обратившимся в турагенство с целью приобретения путевки на морской курорт, были заданы вопросы о значимости для них четырех условий отдыха (переменных). Большая значимость соответствует большему значению переменной. Исследовательская задача состоит в изучении модели взаимосвязей между переменными и выявлении глубинных причин, обуславливающих выбор курорта.
 Критическое значение коэффициента корреляции на уровне значимости 5% при 5 коррелирующих парах равна 0.878. Высокие корреляции в левом верхнем и правом нижнем квадрантах показывают, что взаимосвязаны оценки по стоимости и комфортабельности и оценки по температуре воздуха и температуре воды. Собственные вектора и собственные значения:  Анализ собственных значений, равных соответственно 0.038; 0.004; 1.942; 2.016 показывает, что только для двух факторов значения достаточно велики, чтобы стать предметом дальнейшего рассмотрения. Доля этих факторов в общей дисперсии составляет соответственно 50,4% и 48,5% общей дисперсии, а накопленная дисперсия – 98,9%. 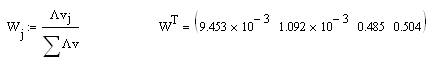 Матрица факторных нагрузок отражает взаимосвязь между факторами и переменными: 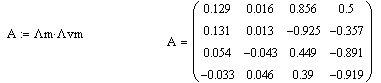 Очевидно, что существенные значения факторных нагрузок наблюдаются только для двух факторов: третий столбец – это корреляции между первым значимым фактором и каждой переменной по очереди, четвертый столбец - корреляции между вторым значимым фактором и каждой переменной. Фактор интерпретируется на основе сильно связанных с ним (имеющих по нему высокие факторные нагрузки) переменных. Так первый фактор – «экономический» (цена+комфорт), а второй - «климатический» (температуры). При этом переменные, имеющие высокие факторные нагрузки по «климатическому» фактору взаимосвязаны положительно (униполярный фактор), а по «экономическому» - отрицательно (биполярный фактор). Необходимо отметить, что выбор знака во время вычислений происходит случайным образом, и знаки не важны сами по себе, а используются для идентификации групп.
Однако, в данном примере, все переменные в значительной степени коррелируют с обоими факторами. Обычно фактор легче интерпретируется, если с ним связана только часть переменных. Вращение Вращение применяется после выделения факторов для максимизации высоких корреляций и для минимизации малых. Существует несколько методов вращения, один из наиболее популярных – метод варимакс, который представляет собой процедуру максимизации дисперсий. Математически это достигается путем умножения матрицы факторных нагрузок на матрицу преобразования:  .Матрица преобразования – это матрица функций угла  , на который выполняется поворот. В двумерном случае После получения окончательной матрицы факторных нагрузок можно получить воспроизведенную матрицу взаимосвязей исходя из формулы  .Разница между исходной и воспроизведенной матрицами называется остаточной матрицей взаимосвязей. При хорошем факторном решении элементы остаточной матрицы должны быть очень малы. Факторные значения После вычисления факторных нагрузок можно вычислить значения факторов для каждого наблюдения. Один из способов – при помощи матрицы коэффициентов факторных значений  . Элементы матрицы – весовые коэффициенты соответствующих значений стандартизированных переменных для расчета значений факторов  .Иначе значения факторов можно рассчитать по формуле  .Высокие отрицательные значения по климатическому фактору свидетельствуют о важности климатического фактора, а высокие отрицательные значения по экономическому фактору означают, что комфорт для респондента важнее фактора стоимости. Так, например, первый респондент получил по первому фактору -0.586, по второму фактору -1.533. Высокое отрицательное значение по «экономическому» фактору свидетельствует о том, что респонденту комфортность важнее, чем низкая стоимость, а высокое отрицательное значение климатического фактора – что климатические условия для него очень важны. Для третьего респондента более привлекательна невысокая цена, чем комфортность, а климатические условия для него не очень важны.
3. Примеры факторного анализа Пример 1. В одном из районов развития гранитоидного магматизма было отобрано 70 проб из грейзенизированных гранитов. В пробах было определено содержание пяти компонент (признаков): SiO2, Na2O, K2O, Li, Be. Результат анализа каждой пробы представляет собой случайную пятикомпонентную величину  , где t- номер пробы; X1,X2, X3, X4, X5 – содержания компонентов SiO2, Na2O, K2O, Li, Be соответственно. Необходимо произвести факторный анализ с целью выяснения геохимических и генетических особенностей объекта. Решение На первом шаге факторного анализа методом главных компонент по выборочной совокупности были вычислены: корреляционная матрица системы используемых признаков (табл.1), её собственные значения, факторные нагрузки и веса факторов (табл.2). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||