9_факторный анализ. 9 факторный анализ
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
Таблица 1Корреляционная матрица
Примечание: коэффициенты корреляции являются значимыми (0,05) при их абсолютном значении не менее 0,532. Таблица 2 Факторные нагрузки, собственные значения и веса факторов
Примечание: факторные нагрузки являются значимыми (0,05) при их абсолютном значении не менее 0,532. Анализ корреляционной матрицы признаков позволяет выявить внутреннюю структуру, которая графически может быть представлена в виде корневой диаграммы (рис.3). 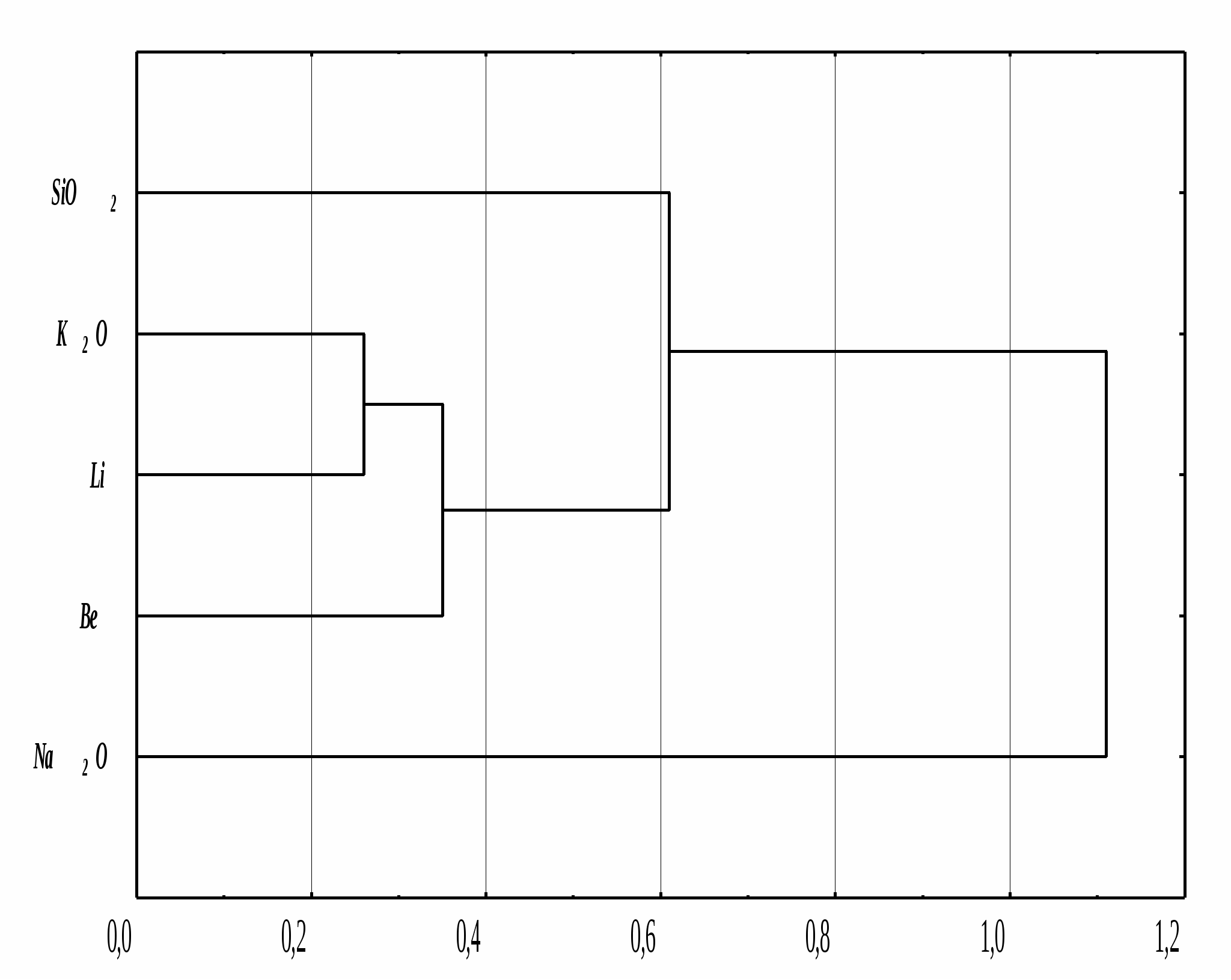 Рисунок 3 Диаграмма связи признаков Величины собственных значений и веса факторов показывают, что значения исследуемых характеристик гранитоидов SiO2, Na2O, K2O, Li, Be определяются преимущественно на 51,4% действием одного фактора F1. Анализ признаковой структуры фактора F1 показывает, что нагрузка этого фактора значимо определяется концентрациями K2O (0,794), Li (0,943), Be (0,695) имеет значимую отрицательную связь с Na2O (-0,558) и более слабую, но положительную связь с SiO2 (0,506). Такой набор признаков и характер их действия позволяет предполагать, что фактор F1 отражает процесс грейзенизации, который протекает с привносом калия, кремния, лития, бериллия и выносом натрия. Фактор F2 несет в себе 26,1% информации о рассматриваемом геологическом объекте. Анализ признаковых нагрузок этого фактора показывает, что он имеет значимую положительную связь с кремнекислотным компонентом SiO2 (0,736) и отрицательные связи со щелочным и щелочноземельными элементами Na2O (-0,609), Be (-0,535), K2O (-0,309), Li (-0,100). Такая признаковая структура фактора F2 позволяет предполагать, что он отражает завершающую стадию процесса грейзенизации – стадию образования кварцевых жил. Фактор F3 несет в себе небольшую долю информации (13,7%) и им можно пренебречь, тем более, что ни одна из нагрузок этого фактора не является значимой. Однако, если задаться целью, проинтерпретировать этот фактор, то можно предположить, что он отражает более низкотемпературный метасоматический процесс, протекавший выше фронта грейзенизации, куда из грейзенизируемых пород выносился натрий. Факторы F4 и F5 являются практически незначимыми и ими можно пренебречь. Однако при более детальном рассмотрении расположения собственных чисел на рисунке 4 видно, что более чем 2 фактора участвует в данном процессе. 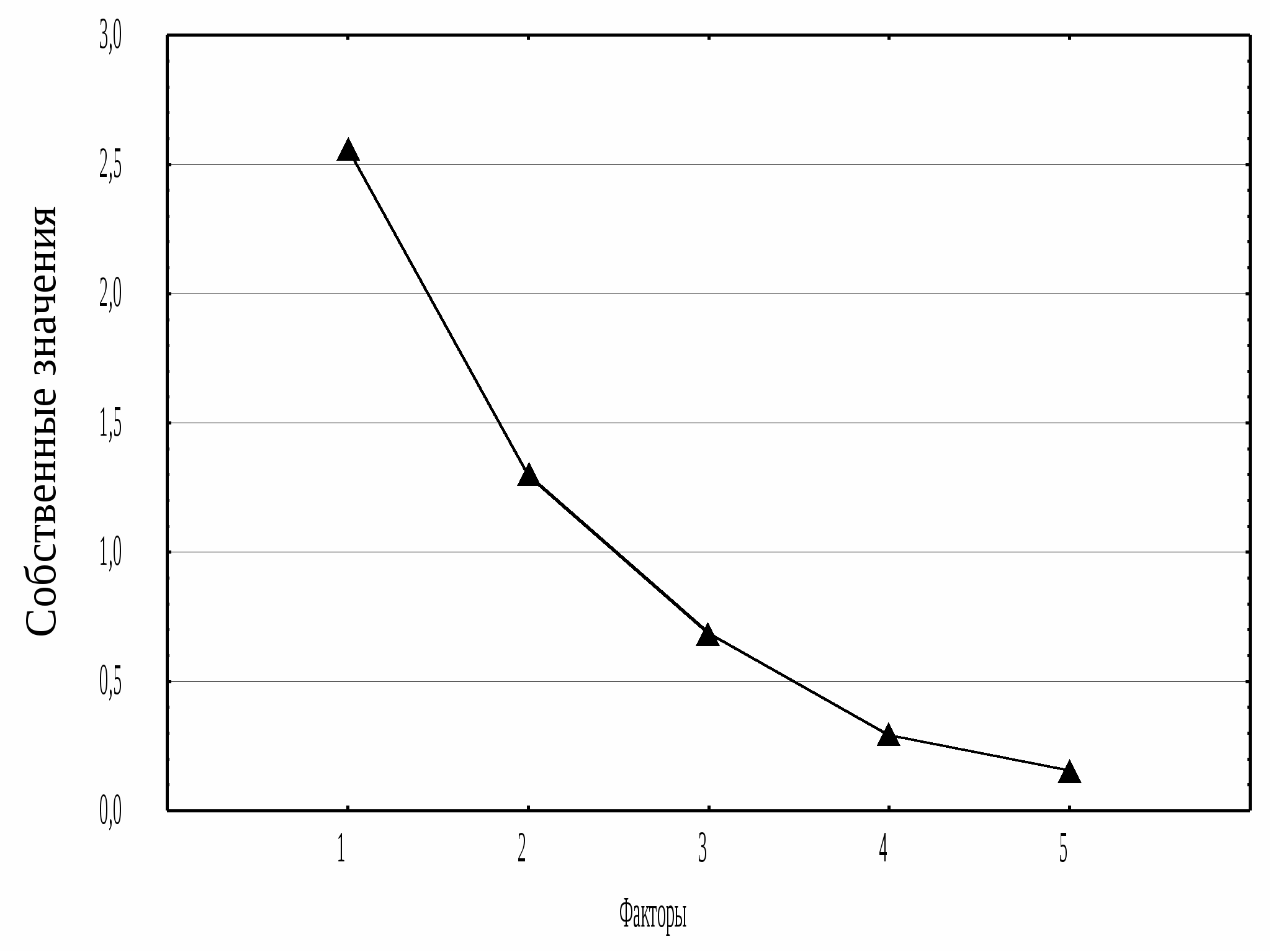 Рисунок 4 Для более четкого выявления структуры факторов можно использовать метод вращения. Окончательное решение должно базироваться на приемлемости с точки зрения научных представлений в данной области. Интерпретация фактора становится проще, если меньшее число признаков будет иметь существенные нагрузки в нем. Один из известных методов «Варимакс» использует критерий, в котором для каждого признака добиваются, чтобы дисперсия квадратов нагрузок фактора была максимальна. Например, в пакете компьютерных программ для обработки и анализа статистической информации «Statistica» введены и другие критерии в зависимости от характера исследуемых объектов и признаков и решаемых задач. В программе требуется заранее ввести число факторов и критерий для вращения. В приближении двух главных факторов мы получаем следующие факторные нагрузки. Таблица 3 Факторные нагрузки, собственные значения и веса факторов после вращения
Первый фактор F1 (44,3%) определяется практически равным вкладом нагрузок K2O (0,838), Li (0,854), Be (0,871), в то время как второй по значимости фактор F2 (32,9%) определяется полярными признаками SiO2 (0,889) и Na2O (-0,811). В приближении трех главных факторов мы получаем следующие факторные нагрузки. Таблица 4 Факторные нагрузки, собственные значения и веса факторов после вращения
Пример 2. В одном из районов Предуралья в песчано-глинистых отложениях в пределах меденосной полосы была пробурена скважина. По керну было отобрано 20 проб, в которых было определено содержание элементов: Cu, Zn, V, Zr, Cорг, Ti. Их концентрации (%) в пробах приведены в таблице 5. Проведем факторный анализ этих данных. Для этого необходимо: найти корреляционную матрицу; выявить главные факторы, обусловившие накопление этих элементов; найти веса (собственные значения) этих факторов и факторные нагрузки; произвести анализ геологической природы выявленных факторов. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
