9_факторный анализ. 9 факторный анализ
 Скачать 0.79 Mb.
|
Таблица 7Корреляционная матрица
Примечание: коэффициенты корреляции являются значимыми (0,05) при их абсолютном значении не менее 0,44. Анализ коэффициентов корреляции показывает, что накопление элемента Cu происходило одновременно с Zn (0,92), Cорг (0,82) и V (0,60), но биполярно и не связано с накоплением элементов Zr и Ti. Содержание элементов Zr и Tiкоррелирует между собой (0,73). Эту связь между элементами можно проиллюстрировать на корневой диаграмме признаков для выявления структуры признаков и предварительного анализа факторов. 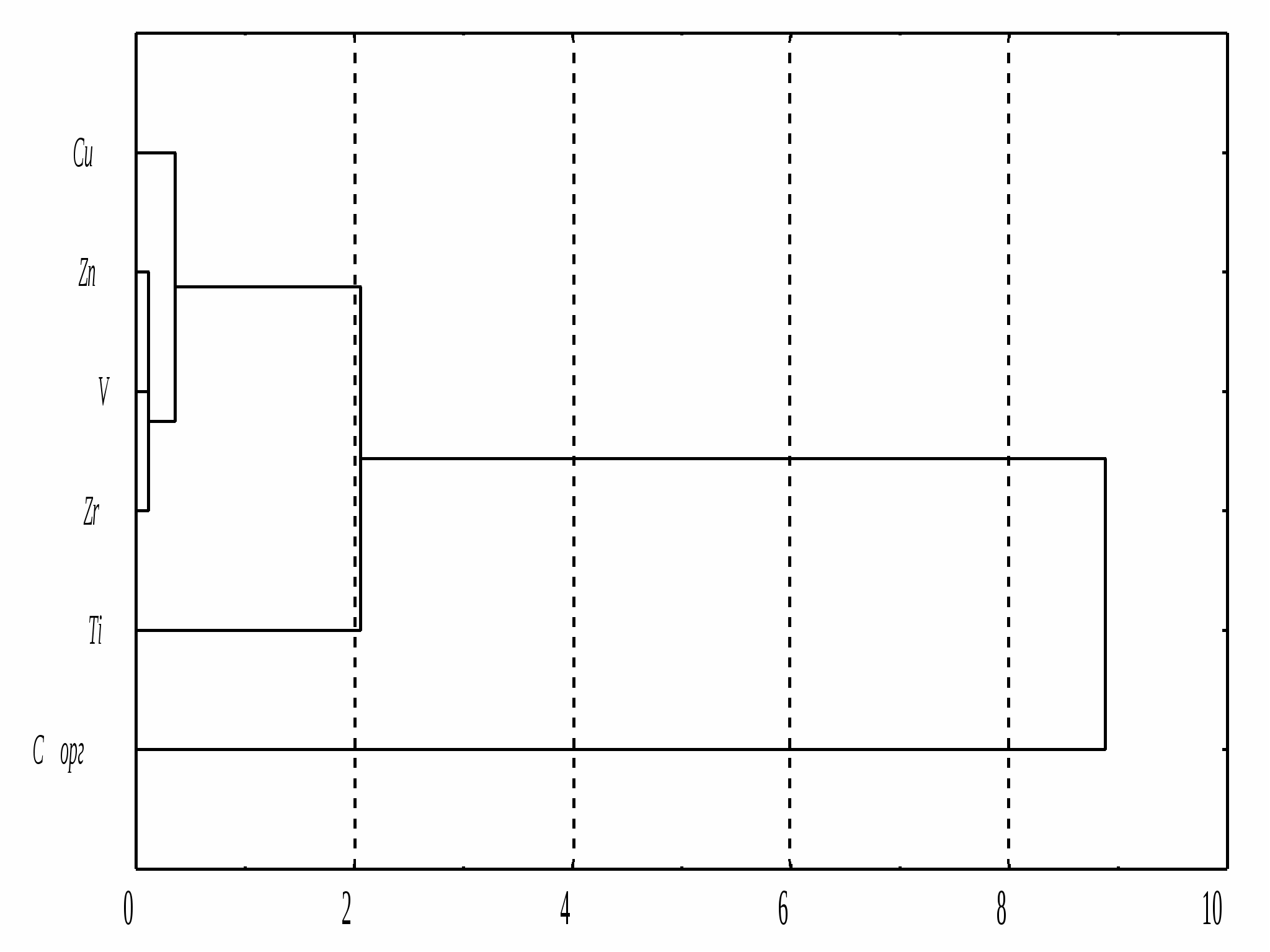 Рисунок 5 Диаграмма связи признаков Основной математический метод выделения факторов и их нагрузок основан на нахождении собственных чисел и собственных векторов корреляционной матрицы. Таблица 8 Факторные нагрузки, собственные значения и веса признаков
Примечание: факторные нагрузки являются значимыми (0,05) при их абсолютном значении не менее 0,44 Величины собственных чисел  (факторные нагрузки  ) и векторов (веса факторов,%) факторной нагрузки признаков табл.7 показывают, что песчано-глинистые отложения характеризуются на 62,78% фактором F1и на 21,06% фактором F2.На первом этапе анализа необходимо определить минимальное число факторов, адекватно воспроизводящие наблюдаемые корреляции. Анализ признаковой структуры преимущественного фактора F1(62,78%) показывает, что нагрузка этого фактора имеет сложный характер и определяется как содержанием элементов Cu (0,893), Zn (0,876), Cорг (0,914), V (0,783) так и значимой отрицательной связью Ti (-0,724). Признаковая структура однополярного фактора F2 (21,06%) характеризует влияние элементов Zr (0,827) и Ti (0,590) на свойства отложения. Влияние элемента V (-0,574) выявляется фактором F3 (8,83%). Наиболее часто число выделяемых факторов определяется количеством собственных чисел больше единицы. В нашем случае это первые два фактора. Другой критерий определяется через графическое изображение собственных чисел. Выделение заканчивается на том факторе, после которого исследуемая зависимость близка к горизонтальной линии. Как видно на рисунке 6, выделяется не более 4 факторов. Окончательное решение должно базироваться на приемлемости с точки зрения научных представлений в данной области.  Рисунок 6 Следующим шагом с помощью процедуры вращения выявляются наиболее легко интерпретируемые факторы. Существует три подхода к этой проблеме. Геометрический подход используется, когда число факторов не более двух и имеются отдельные скопления (кластеры) признаков. Аналитический – выбирается критерий, на основе которого производится вращение (ортогональное или косоугольное) осей. В третьем подходе задается априорная целевая матрица, соответствующая предполагаемой факторной структуре. Целью всех вращений является получение наиболее простой факторной структуры или достижение простоты интерпретации признаков и факторов. 1. Рассмотрим случай выделения двух факторов и для вращения будем использовать метод «Варимакс» в предположении, что он дает лучшее разделение факторов. Таблица 9 Факторные нагрузки, собственные значения и веса признаков после вращения
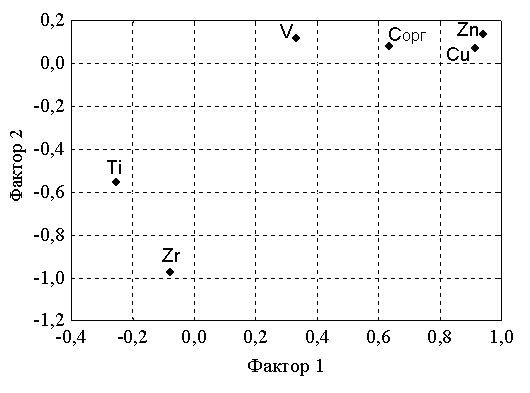 Рисунок 7 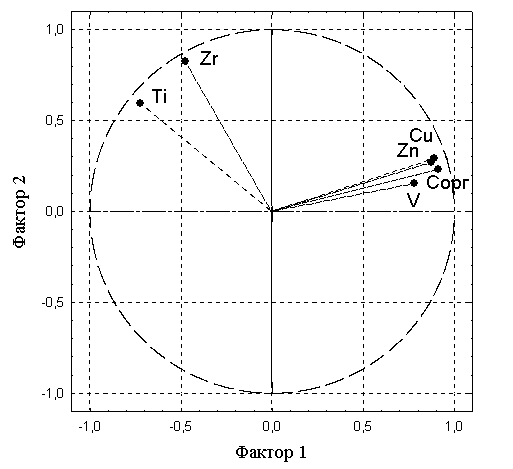 Рисунок 8 В отличие от исходной системы координат теперь факторы разделены на биполярные группы признаков, у которых имеется общая направленность и интерпретируемость (рис. 7,8). В исходных данных можно выделить дополнительные сходные и отличительные свойства. 2. Выделяем три фактора и видим, что элемент V по своим свойствам выделяется из первого фактора в отдельный третий факторF3, а элементCорг распределилось по факторам F1и F3. В новых координатах можно провести дополнительные исследования свойств залежи. Таблица 10 Факторные нагрузки, собственные значения и веса факторов трех признаков после вращения
3. Задаем требование – выделить четыре фактора и произвести вращение системы координат. Таблица 11 Факторные нагрузки, собственные значения и веса факторов четырех признаков после вращения
В новой системе координат четвертый фактор F4 определяет накопление Tiв отложениях, однако с такой же долей участия этот элемент входит во второй фактор F2. Видимо, такое положение происходит из-за избыточности четвертого фактора F4. Таким образом, как следует и из графического представления и численных вычислений, два-три фактора наиболее полно характеризуют признаковую структуру данных отложений (рис.9) 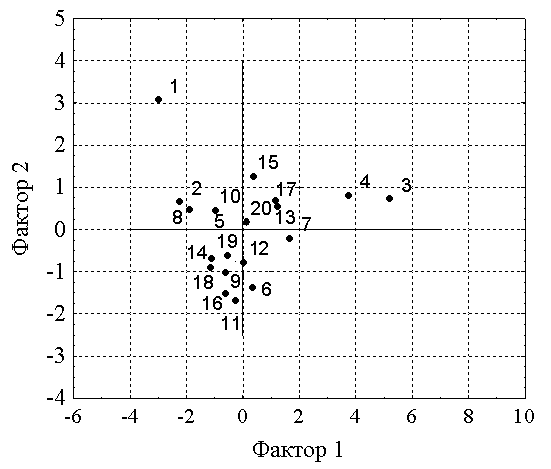 Рисунок 9 Вывод Анализ признаковой структуры трех выявленных факторов позволяет предполагать, что фактор F1 может быть интерпретирован как действие сульфидного диагенеза в осадке, вызванного разложением органики в анаэробной среде и развитием процессов бактериальной сульфатредукции. С этим процессом и связано образование сульфидов меди, цинка, накопление Сорг. Кроме того, органика выступает еще и как концентратор ванадия, что описывается фактором F3. Фактор F2 может быть интерпретирован как терригенное накопление в осадке аллотигенных минералов титана и циркония. ЗАКЛЮЧЕНИЕ Проведенное рассмотрение показывает, что факторный анализ позволяет не только выявлять причинно-следственные взаимосвязи различных признаков изучаемых геологических объектов, но и решать разнообразные генетические вопросы путем выявления главных действующих факторов, анализа их признаковой структуры и анализа факторной структуры изучаемых признаков различных геологических образований. Более того, метод позволяет воссоздать в факторном координатном пространстве облик изучаемого геологического объекта и указать его характерные признаки и отличительные особенности. Литература
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
