9_факторный анализ. 9 факторный анализ

• Название: 9 факторный анализ
• Анкор: 9_факторный анализ.doc
• Дата: 12.02.2018
• Размер: 0.79 Mb.
• Имя файла: 9_факторный анализ.doc
• Тип: Документы; #15473
• страница: 5 из 10

Проблема числа факторов

Процедура факторного анализа предполагает предварительное задание числа факторов. Поэтому на первом, поисковом, этапе имеет смысл использовать анализ главных компонент. Для выбора числа факторов обычно применяют следующие подходы:

1. 
   Критерий Кайзера или критерий собственных чисел. Этот критерий предложен Кайзером, и является, вероятно, наиболее широко используемым. Отбираются только факторы с собственными значениями равными или большими 1. Это означает, что если фактор не выделяет дисперсию, эквивалентную, по крайней мере, дисперсии одной переменной, то он опускается.
   
2. 
   Критерий каменистой осыпи или критерий отсеивания. Он является графическим методом, впервые предложенным психологом Кэттелом. Собственные значения можно изобразить в виде простого графика. Кэттел предложил найти такое место на графике, где убывание собственных значений слева направо максимально замедляется.
   

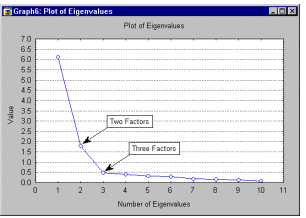Предполагается, что справа от этой точки находится только «факториальная осыпь» — «осыпь» является геологическим термином, обозначающим обломки горных пород, скапливающиеся в нижней части скалистого склона. Однако этот критерий отличается высокой субъективностью и, в отличие от предыдущего критерия, статистически необоснован. Недостатки обоих критериев заключаются в том, что первый иногда сохраняет слишком много факторов, в то время как второй, напротив, может сохранить слишком мало факторов; однако оба критерия вполне хороши при нормальных условиях, когда имеется относительно небольшое число факторов и много переменных. На практике возникает важный вопрос: когда полученное решение может быть содержательно интерпретировано. В этой связи предлагается использовать ещё несколько критериев.

3. 
   Критерий доли воспроизводимой дисперсии. Факторы ранжируются по доле детерминируемой дисперсии, когда процент дисперсии оказывается несущественным, выделение следует остановить. Желательно, чтобы выделенные факторы объясняли более 80 % разброса. Недостатки критерия: во-первых, субъективность выделения, во-вторых, специфика данных может быть такова, что все главные факторы не смогут совокупно объяснить желательного процента разброса. Поэтому главные факторы должны вместе объяснять не меньше 50,1 % дисперсии.
   
4. 
   Критерий интерпретируемости и инвариантности. Данный критерий сочетает статистическую точность с субъективными интересами. Согласно ему, главные факторы можно выделять до тех пор, пока будет возможна их ясная интерпретация. Она, в свою очередь, зависит от величины факторных нагрузок, то есть если в факторе есть хотя бы одна сильная нагрузка, он может быть интерпретирован. Возможен и обратный вариант — если сильные нагрузки имеются, однако интерпретация затруднительна, от этой компоненты предпочтительно отказаться.
   
5. 
   На практике возникает важный дополнительный вопрос, а именно: когда полученное решение может быть содержательно интерпретировано. Поэтому обычно исследуется несколько решений с большим или меньшим числом факторов, и затем выбирается одно наиболее "осмысленное. Окончательное решение о числе факторов принимается после их интерпретации.
   

2. Методы (алгоритмы) факторного анализа

Факторный и компонентный анализ в большинстве случаев проводятся совместно.

Компонентный анализ является методом определения структурной зависимости между случайными переменными. В результате его использования получается сжатое описание малого объема, несущее почти всю информацию, содержащуюся в исходных данных. Главные компоненты получаются из исходных переменных путем целенаправленного вращения, т.е. как линейные комбинации исходных переменных. Вращение производится таким образом, чтобы главные компоненты были ортогональны и имели максимальную дисперсию среди возможных линейных комбинаций исходных переменных X. При этом переменные не коррелированы между собой и упорядочены по убыванию дисперсии (первая компонента имеет наибольшую дисперсию). Кроме того, общая дисперсия после преобразования остается без изменений.

Факторный анализ является более общим методом преобразования исходных переменных по сравнению с компонентным анализом.

Как правило, применение методов факторного анализа включает три этапа:

• 
  выделение первоначальных факторов;
  
• 
  вращение выделенных факторов с целью облегчения их интерпретации в терминах исходных переменных (в частности, для исключения отрицательных значений);
  
• 
  содержательная интерпретация новых факторов в предметных терминах, что является творческой задачей исследователя, выходящей за рамки предлагаемого формального метода.
  

Наиболее часто факторный анализ используется для выявления в наблюдаемых признаках  некоторых латентных (скрытых) переменных, называемых факторами. Гипотеза о наличии этих факторов основана на предположении о существовании чего-то общего в наблюдаемых признаках. Выводимые гипотетические факторы обладают следующими свойствами:

1. Они образуют линейно независимый набор переменных, т.е. ни один из факторов (компонент) не выводится как линейная комбинация остальных.

2. Переменные, являющиеся гипотетическими факторами, можно разделить на два основных вида – общие и характерные факторы. Они отличаются структурой весов в линейном уравнении, которое выводит значение наблюдаемой переменной из гипотетических факторов. Общий фактор имеет несколько переменных с ненулевым весом или факторной нагрузкой, соответствующей этому фактору. При этом фактор называется общим, если хотя бы две его нагрузки значительно отличаются от нуля. Характерный фактор имеет только одну переменную с ненулевым весом (т.е. только одна переменная от него зависит).

3. Всегда предполагается, что общие факторы не коррелируют с характерным фактором, также характерные факторы не коррелированы между собой.

4. Обычно предполагается, что число общих факторов меньше, чем число наблюдаемых переменных, однако число характерных факторов принимают равным числу наблюдаемых переменных.

Естественно, факторы не будут содержать всю дисперсию переменных; они будут содержать только ту часть, которая принадлежит общим факторам и распределена по нескольким переменным. На языке факторного анализа доля дисперсии отдельной переменной, принадлежащая общим факторам (и разделяемая с другими переменными) называется общностью. С общей точки зрения в качестве оценки общности следует использовать множественный коэффициент корреляции выбранной переменной со всеми.

Основной результат факторного анализа – выявление факторной структуры, элементами которой являются факторные нагрузки. Факторные нагрузки вычисляются таким образом, чтобы восстановленные коэффициенты корреляции минимально отличались от исходных корреляций.

Алгоритмы факторного анализа обеспечивают максимально возможное приближение восстановленных коэффициентов корреляции к исходным. Это достигается варьированием числа факторов и диагональных элементов корреляционной матрицы, на которой располагаются общности.

Алгоритмы факторного анализа – это различные способы получения факторной структуры при заданном числе факторов. За исключением метода главных компонент все процедуры факторного анализа являются итеративными и эмпирическими. Они направлены на получение оценок общностей и факторных нагрузок. В процессе итераций воспроизведенная корреляционная матрица должна быть максимально приближена к исходной.

Таблица 9.1 Алгоритмы факторного анализа

Метод	Описание
Факторный анализ образов	Метод главных компонент применяется к редуцированной корреляционной матрице, у которой на главной диагонали в качестве оценок общности расположены квадраты коэффициентов множественной корреляции.
Метод главных осей	Итеративный пересчет собственных значений и факторных нагрузок исходя из предыдущих значений общностей. Окончание расчета – по числу итераций или по достижению заданного изменения значений общностей.
Метод невзвешенных наименьших квадратов	Итеративная процедура пересчета факторной структуры и восстановленных корреляций с целью минимизации квадратов разностей исходной и воспроизведенной корреляционной матриц. На первом шаге общности рассчитываются как квадраты коэффициентов множественной корреляции.
Обобщенный метод наименьших квадратов	Отличается от предыдущего тем, что для каждой переменной вводят веса тем большие, чем больше общность переменной.
Метод максимального правдоподобия	Расхождения исходной и воспроизведенной корреляций проверяются при помощи критерия , и если отклонение значимо, то число факторов увеличивается на 1.

Анализ главных компонент дает наиболее грубое решение. Метод максимального правдоподобия позволяет статистически оценить минимально возможное число факторов. При этом наиболее предпочтительно, чтобы каждая переменная после вращения находилась вблизи оси фактора, то есть имела бы максимальную нагрузку по одному фактору и минимальные по остальным. В этом случае каждая переменная будет соотнесена только с одним фактором.