Лыкин. 317_Лыкин(1). А. Г. Русина Работа подготовлена на кафедре

• Название: А. Г. Русина Работа подготовлена на кафедре
• Анкор: Лыкин
• Дата: 26.01.2023
• Размер: 1.85 Mb.
• Имя файла: 317_Лыкин(1).doc
• Тип: Документы; #906398
• страница: 3 из 10

1.3. Переменные в математических моделях

Переменные величины, входящие в математическую модель, различают по нескольким признакам.

По роли, которую переменные играют по отношению к объекту моделирования. На рис. 1.4 X = (x₁, x₂,…, x_n) – вектор входных переменных, Y = (y₁, y₂,…, y_m) – вектор выходных переменных. В связи с разделением переменных на входные и выходные рассматриваются прямые и обратные задачи исследования объекта по его математической модели. В прямых задачах по данным о выходах объекта иссле-дуется его поведение в различных условиях (режимах работы), т. е.
входные переменные, структура и параметры модели относятся к исходным данным, а выходные переменные представляют результат исследования: Y = f(X) или F(X, Y) = 0, где известны характеристики X и f или F.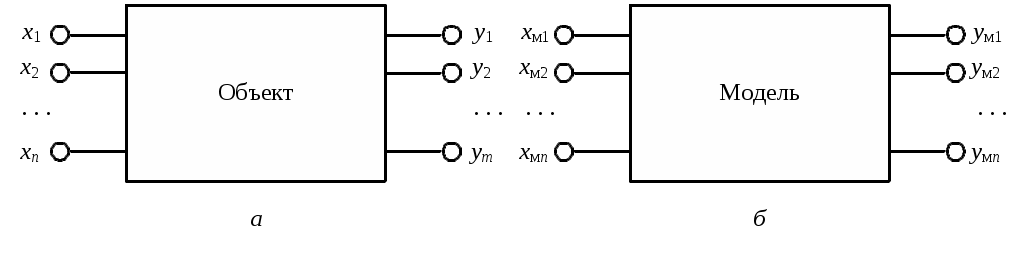


а б

Рис. 1.4. Переменные в объекте и его модели

В обратных задачах считаются известными X и Y (доступны для измерения и исследования), а определению подлежат неизвестные структура и параметры модели (f или F). Такие задачи называют задачами идентификации.

Входные переменные разделяют на управляемые (управляющие воздействия) и неуправляемые (возмущения) Первые позволяют выполнять регулирование режима работы объекта, а вторые меняются самопроизвольно, например погодные условия.

По подверженности воздействию случайным факторам. Детерминированная (определенная) переменная означает, что для нее исключено влияние случайных факторов – она задается вполне определенным значением или меняется во времени по определенному закону. Некоторые переменные по своей природе или по влиянию на них случайных факторов являются случайными величинами. Процесс изменения такой величины во времени называется случайным или стохастическим процессом. К этим переменным можно отнести мощность нагрузки тяговой подстанции, которая зависит от загрузки контактной транспортной сети, или величину активного сопротивления провода ЛЭП, в большой степени подверженного влиянию температуры окружающей среды.

В основе описания случайных переменных лежат методы теории вероятностей, случайных процессов и математической статистики.

По свойствам непрерывности и дискретности. Изменения непрерывных переменных во времени описываются непрерывными функциями, которые могут принимать континуальное множество значений в некоторых практически всегда имеющихся пределах (рис. 1.5, а). Непрерывность, порожденная инерционностью материальных систем, является их неотъемлемым свойством. Однако на практике возможности разрешения близких значений функций и ее аргументов всегда ограничены; для каждого конкретного случая можно указать определенную область, в пределах которой эти значения становятся неразличимыми для наблюдателей или инструментальных средств. Очевидно, что такую область достаточно характеризовать единственным значением, что приводит к понятию дискретных переменных (рис. 1.5, б, в, г).

Дискретные переменные подразделяются на три типа:

1) дискретные относительно значений переменной (рис. 1.5, б);

2) дискретные относительно времени (рис. 1.5, в);

3) дискретные относительно значений переменной и относительно времени (рис. 1.5, г).

Множество дискретных значений, которые принимает переменная, как правило, является конечным: положение выключателя (включено, выключено), количество включенных генераторов на электростанции (0, 1, 2, … ), значения целых чисел, представленных в цифровой вычислительной машине (например, от –32 768 до +32 767). С помощью дискретных переменных относительно значений удобно представлять некоторые процессы (графики нагрузок или напряжений по часам
суток или месяцам года), распределение вероятностей (гистограмма)
и т. п.

Дискретность во времени связана с отсчетом или замером переменных в отдельные дискретные моменты времени. Так, в автоматизированных системах управления измерения переменных выполняются с заданной периодичностью, например, через каждые 5 минут.

а

б

в

г


Рис. 1.5. Виды переменных по свойствам непрерывности и дискретности

Дискретность по времени и по значению дополнительно к измерениям в отдельные моменты времени предполагает использование дискретных значений переменных.

По способу получения переменные подразделяются на наблюдаемые и ненаблюдаемые.

Главное свойство наблюдаемых переменных – доступность для наблюдения. Однако наблюдаемость сама по себе еще не обеспечивает возможности полного исследования и описания переменной. Необходимо, чтобы последняя обладала еще свойством измеримости, т. е. возможностью построения для исследуемой величины метрики. Этому требованию удовлетворяют непосредственно измеряемые переменные. Они представляют собой количественные характеристики свойств и параметров всевозможных материальных объектов и процессов (напряжение, ток, скорость, линейные размеры и пр.), которые определяются на основе прямого измерения, т. е. сравнения с мерой, обеспечены средствами измерения и охвачены существующей системой метрологического обеспечения.

Тесно связан с непосредственно измеряемыми и следующий класс переменных – косвенно измеряемые.

Косвенно измеряемая переменная x сама по себе не является объектом измерения, а часто и в принципе не может быть непосредственно измерена. Вместо нее непосредственному измерению подвергаются другие, вспомогательные переменные (α, β, γ,…), которые связаны с исследуемой переменной функциональной зависимостью x = f(α, β, γ,…). Это позволяет вычислить значение искомой переменной по результатам прямых наблюдений вспомогательных величин, например, вычислить объем тела по результатам измерения его линейных размеров. При испытаниях силовых трансформаторов в электрических сетях температуру его обмоток определяют методом измерения их сопротивлений постоянному току, т. е. температура – косвенно измеряемая переменная.

К косвенно измеряемым переменным относят такие искусственно сконструированные идеальные образования, которые вообще не наблюдаемы: математическое ожидание, дисперсия, энтропия и др.

Существует класс переменных, которые при их количественном оценивании не имеют материальной эталонной базы и находятся вне сферы метрологии. К ним относятся все виды непосредственно или косвенно измеряемых переменных, приведенных к безразмерной форме и выраженных в относительных единицах. Например, некоторые величины материальной природы (интенсивность сейсмических явлений, интенсивность облачности в метеорологии, твердость материалов по Бринеллю и некоторые другие), а также искусственные идеальные конструкции, характеризующие в количественном отношении сложные и массовые объекты и явления (рентабельность, прибыль, эффективность и др.). Такие переменные называют условно измеряемыми, так как меры или единицы измерения, используемые при их количественном оценивании, носят конвенционный характер.

Существует еще один класс наблюдаемых переменных – условно количественно оцениваемые. Они представляют сложные многофакторные явления, интенсивность которых может быть различной, но для количественного оценивания этой интенсивности не удается ввести ни объективной единицы измерения, ни способа измерения. Однако в целом ряде случаев между интенсивностями рассматриваемого явления удается установить отношение порядка (равны – не равны, больше – меньше и т. д.), а затем отобразить эти отношения, вообще говоря, произвольным образом на некоторое множество (систему) чисел. Результатом такой процедуры являются, например, численные оценки качества усвоения учащимися и студентами учебного материала, степень удовлетворения работой членов некоторого производственного коллектива, степень качества исполнения музыкального произведения или выполнения спортивного упражнения. Условное количественное оценивание основано на опыте и интуиции и по сути своей субъек-тивно.

Ненаблюдаемые переменные подразделяют на принципиально ненаблюдаемые и технически ненаблюдаемые.

Принципиально ненаблюдаемые переменные не существуют как компоненты реального мира и поэтому поддаются определению только косвенными методами, в частности на основе косвенных измерений (статистические характеристики).

Технически ненаблюдаемые переменные характеризуют такие материальные явления, которые либо не обеспечены техническими средствами, необходимыми для измерения и оценивания, либо протекают в условиях, когда инструментальный доступ к ним невозможен. Характерным примером переменной, не наблюдаемой из-за практической недоступности, является количество угля для помола в шаровой мельнице на электростанции.

Каждая переменная, связанная с материальным объектом, может изменять свои значения лишь в некоторых конечных пределах, которые обусловлены физическими свойствами объекта и характером решаемой задачи. Данные об этих пределах – ограничения на переменные – существенны при построении и использовании всех видов моделей, а в оптимизационных задачах, где необходимо найти оптимальное значение так называемой целевой функции, ограничения являются главной частью самой модели.

С математической точки зрения различают ограничения типа простых неравенств: X_min ≤ X ≤ X_max, Y_min ≤ Y ≤ Y_max – параллепипедные ограничения и функциональные ограничения, фиксирующие предельные значения некоторой величины в функции от других переменных: f_min(X) ≤ Z ≤ f_max(X) и т. п.

В практике моделирования выделяют так называемые жесткие ограничения, которые являются абсолютными (например, угол поворота лопатки турбины – «до упора»), и ограничения мягкие, допускающие кратковременные нарушения установленной границы значений переменной (например, верхнего предела рабочего напряжения на электродвигателе).

В общем случае данные об ограничениях на переменные входят в состав модели как обязательная составная часть.