Поручиков М.А. Анализ данных. А. поручиков

• Название: А. поручиков
• Дата: 25.10.2022
• Размер: 2.76 Mb.
• Имя файла: Поручиков М.А. Анализ данных.docx
• Тип: Анализ; #753011
• страница: 18 из 20

БЫСТРОДЕЙСТВИЕ СИСТЕМ АНАЛИЗА ДАННЫХ

Общие сведения

При проектировании систем анализа данных важно представлять, какое время будет затрачено на решение вычислительных задач. В общем случае быстродействие систем анализа данных зависит от многих факторов:

• 
  вычислительной сложности использованных алгоритмов;
  
• 
  способа программной реализации алгоритмов;
  
• 
  аппаратного обеспечения.
  

Вычислительная сложность

Вычислительная сложность – это зависимость трудоемкости вычислений от объема обрабатываемых данных. Например,

вычислительная сложность алгоритма линейного поиска

O(n)  n^,

^{а алгоритма бинарного поиска –} O(n)  log n

(рис. 52).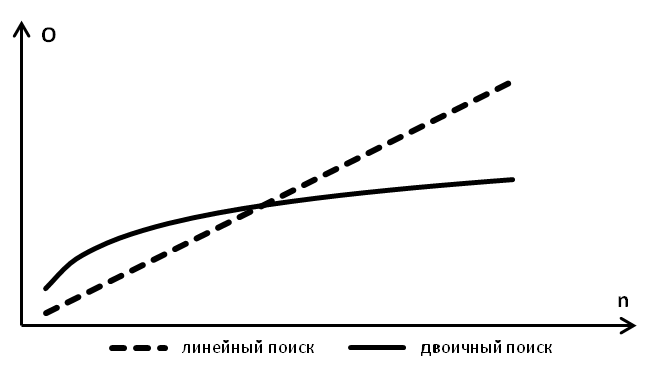

Рис. 52. Вычислительная сложность алгоритмов поиска
Очевидно, что один и тот же объем данных будет обработан быстрее алгоритмом с меньшей вычислительной сложностью.

Например, вычислительная сложность алгоритма вычисления

произведения матриц «по определению»

O(n)  n³ , а алгоритма

Штрассена – O(n)  n^2,81 . Очевидно, что один и тот же объем данных будет обработан быстрее алгоритмом с меньшей вычислительной сложностью

Предположим, что имеются два алгоритма, имеющие

соответственно вычислительную сложность

O₁ (n)

и O₂ (n) . Для

сравнения их вычислительной сложности необходимо найти значения предела

lim <sup>O1 (n) . (24)

n</sup> O₂ (n)

При этом если значение выражения (24):

• 
  равно  , то вычислительная сложность функции чем вычислительная сложность функции O₂ (n) ;
  
• 
  равно 0, то вычислительная сложность функции чем вычислительная сложность функции O₁(n) ;
  

O₁ (n)
O₂ (n)

больше, больше,

• 
  равно некоторому числу, то функции одинаковую вычислительную сложность.
  

Пример

O₁ (n)

и O₂ (n)

имеют

Пусть имеются два алгоритма с вычислительной сложностью

соответственно O(n)  eⁿ, O(n)  n² , тогда

1 2

n
lim ^O1(n)  lim ^e
 lim

eⁿ^



 lim ^e
  .

2
^n O₂ (n)

n _n

n _{n2 }



n
n _2n

Следовательно, вычислительная сложность первого алгоритма больше вычислительной сложности второго алгоритма.

Экспериментальноеопределениевычислительнойсложности

Допустим, что реализован некоторый модуль системы анализа данных, предназначенный для обработки информации. Для использования этого модуля в реальных задачах необходимо четко представлять его вычислительную сложность.

Для определения вычислительной сложности необходимо провести эксперимент, в ходе которого нужно измерить время обработки этим модулем некоторого объема исходных данных.

В результате эксперимента будут получены точки вида «объем данных - время обработки» (рис. 53, а). Аппроксимировав экспериментальные данные какой-либо функцией, можно построить прогноз трудоемкости вычислений для любого, в том числе большего объема данных (рис. 53, б).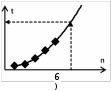



Рис. 53. Прогнозирование вычислительной сложности
Программноеобеспечениеsquare_matrix_multiply

Программное обеспечение square_matrix_multiply предназначено для исследования факторов быстродействия систем анализа данных на примере операции умножения квадратных матриц. Пользователь может варьировать размеры матриц, количество вычислительных потоков (рис. 54). Дополнительно может быть задан размер серии экспериментов. Программное обеспечение выполняет ряд экспериментов, в ходе которых проводится измерение времени, затраченного на умножение матриц.




Программное обеспечение square_matrix_multiply
Размер матриц

Число потоков Размер серии

Время вычислений

Рис. 54. Схема эксперимента
Программное обеспечение реализовано в виде приложения для операционной системы Windows (рис. 55).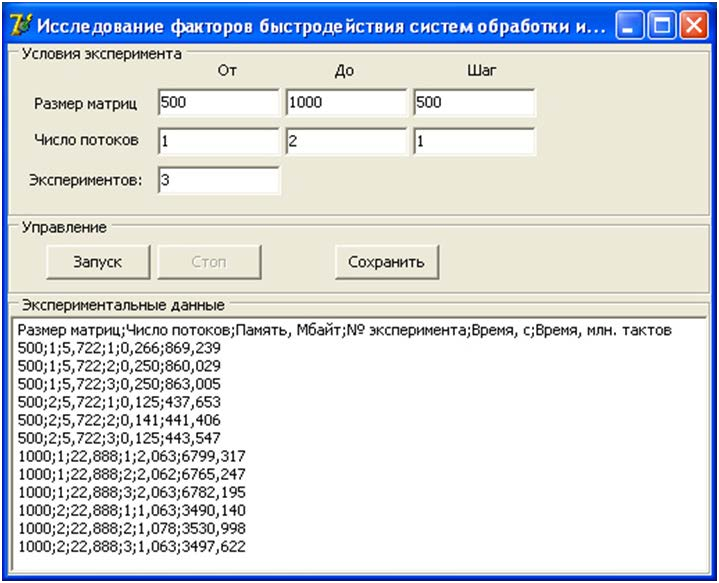

Рис. 55. Интерфейс программного обеспечения square_matrix_multiply
Запуск эксперимента производится нажатием кнопки «Запуск». Результатом эксперимента является набор данных, включающий как условия эксперимента, так и экспериментальные данные. Результаты эксперимента можно сохранить в текстовый файл формата csvс помощью нажатия кнопки «Сохранить». Прервать выполнение экспериментов можно с помощью кнопки «Стоп».