Поисковые мероприятия БЛА. Диплом.Ворд. А. В. Сытин Р. Н. Поляков Орёл, 2020 г

• Название: А. В. Сытин Р. Н. Поляков Орёл, 2020 г
• Анкор: Поисковые мероприятия БЛА
• Дата: 02.03.2023
• Размер: 1.19 Mb.
• Имя файла: Диплом.Ворд.docx
• Тип: Документы; #965645
• страница: 10 из 19

Динамические уравнения

Вектор скорости квадрокоптера в инерциальной системе обозначим v, тогда Второй закон Ньютона примет вид:



(3.10)
dv

m_n — = F
o _dt

где m_o - общая масса устройства, кг;

F - вектор суммарной силы, приложенной к нему, Н.

При переходе от неподвижной системы координат в подвижную, закон преобразуется следующим образом:


(3.11)
dv ,dvV . _ч

m_n — = m_n (+ w х v) = F„
o dt o^y dt ^{в в}

где ^v - линейное ускорение устройства относительно подвижной системы

dt

координат;

w - угловая скорость вращения подвижной системы относительно инерциальной, рад/с.

Управляющая сила вычисляется и прикладывается в подвижной системе

координат, соответственно получаем следующее выражение:







V „

_х,в

v_z,₅J

™у, в Рв_х, в Ч^у, в

qvz, в

^П', в

Pvy,в _

1

1- —

m_o

(3.12)

Второй закон Ньютона при вращательном движении в Земной неподвижной

системе принимает следующий вид:


(3.13)
dL

— = M
dt

где L - угловой момент, кг ■ м² /с;

М - момент вращения силы, Н ■ м.

При переходе от неподвижной системы координат в подвижную, закон преобразуется следующим образом:


(3.14)
dL d L

= + w х L = M_R

dt dt ^в

где L = JwB, a J - тензор инерции.

Изм.	Лист	№ докум.	Подпись	Дата

Примем квадрокоптер в качестве шара с радиусом Rk, и массой Mk. От центра данного шара, на расстоянии l, расположены материальные точки с массой m (рис. 3.3).


Рисунок 3.3 - Схематичное представление квадрокоптера

Принимаем квадрокоптер за симметричное тело, тогда тензор инерции будет иметь следующий вид:

(3.15)

где J_x, J_y, J_z - компоненты тензора, которые находятся по формулам:





J =J

2MR² 2

k-k- + 27² 2т

5

(3.16)

(3.17)
2M_kR_k² 2

J = k-k- + 47² _т

z₅

Получаем, что угловые ускорения находятся следующим образом:

р		(	’0	-	- q	■ Jx	0	0 ■	p
q			- -	0	p	0	Jy	0	q	+ MBT	(3.18)
г _			_q	-p	0	0	0	Jz _	_ - _	)

(3.19)
Представим M_B^T в виде:

					ВКР.20.15.04.06.О. Н.00.000 РПЗ	Лист
						55
Изм.	Лист	№ докум.	Подпись	Дата

MB<sup>T


т</sup>?

*6 ^Tv _

Тогда окончательно получаем, что угловые ускорения равны:

(3.20)

3. 
   Модель для управления
   

Добавим к модели квадрокоптера (формулы 3.7 - 3.9, 3.12, 3.20) выражения, описывающие силы и крутящие моменты, действующие на устройство (рис. 3.4).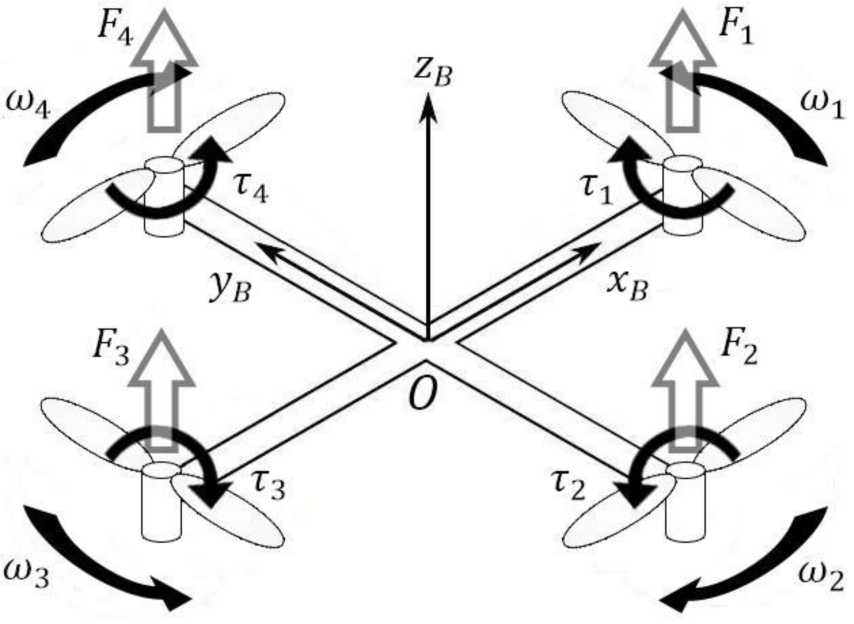



Рисунок 3.4 - Действующие на квадрокоптер силы и крутящие моменты

Подъемная сила и крутящие моменты винтов прямо пропорциональны квадрату скорости их вращения [20] и находятся по следующим формулам:

F = k (^2 + (2 + о₃² + ^²) (3.21)

7,=lk (m2	- mj)	(3.22)
тв = lk (mj-	— ®2)	(3.23)
=ь (—mm+m^	— mf + m^)	(3.24)

где mi - скорость вращения i-го винта, рад/с;


k, b - постоянные, определяемые экспериментально. На квадрокоптер действует сила тяжести:


Fg =


(3.25)


В подвижной системе координат формула 3.25 примет следующий вид:


FgB =


m_og sine

- m_og sin <pcosO

- m_og cos^cosO


Подставим полученные выражения в формулу 3.12 и получаем:


(3.26)

V p		, B	- qvz, в		“ 0 ■	+F	PsinO I - sin (pcosO
Vv.»	=	PVz, B	- rvx, B	- g	0			(3.27)
						m^
v,B_		_QBX, B	- Pvy, B _		L1 J	o	- cos ^ cos O

Считаем, что углы (р и в малы и ими можно пренебречь, тогда формула 3.9


принимает следующий вид:


(3.28)


Аналогично считаем, что компоненты qr, pr, pq формулы 3.20 малы, тогда


получаем:

Изм.	Лист	№ докум.	Подпись	Дата

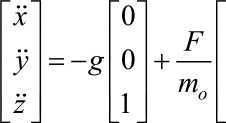1 Л^Т

1

Г^те


(3.29)


С учетом данного выражения, получаем, что производная 3.28 будет


следующей:


1

J,^Тф

1

Г^те


Пренебрегая R продифференцируем формулу 3.7:

x у =RV_B z


(3.30)


(3.31)


Инерциальная система является неподвижной, тогда формулу 3.27 можно подставить в формулу 3.31, отбросив первое слагаемое:


cos ф sin в cos ф + sin ф sin ф sin ф sin в cos ф - cos ф sin ф cospcosO


(3.32)


К данной системе необходимо дополнить силу аэродинамического сопротивления [6]:


F = c_d — S

a d


(3.33)


где c_d - коэффициент аэродинамической силы;


р - плотность воздуха, кг/м³;


v - скорость набегающего потока воздуха, м/с;

S - площадь поверхности аппарата, на которую воздействует набегающий поток, м 2 Совместив все выражения получаем следующую математическую модель квадрокоптера: Г.. , . „ . . , F . ох2 _ X = (cos ЦТ sin 0 COS (р + sin Sin (р) sign(x)cd —— Sx т0 2 .. z • . Л . 4 F . yx у = (sin \p sin в cos (p - cos ip Sin (p) sign(x)cd S •• nF ■ c\ Pzl Q Z - COS фcos 0 g- sign(z)cd Sz J 2 (3.34) ё=ТТв y; Таким образом, описываются линейные и угловые ускорения, а следовательно, и местоположение квадрокоптера.
					ВКР.20.15.04.06.0.11JJO0JOO РПЗ	Лист
						59
Изм.	Лист	№ докум.	Подпись	Дата