Поисковые мероприятия БЛА. Диплом.Ворд. А. В. Сытин Р. Н. Поляков Орёл, 2020 г
 Скачать 1.19 Mb. Скачать 1.19 Mb.
|
|
l - максимальная длина выхода внутренней капсулы, м. Произведем расчет: M = 2000 -1,9 = 3800 Н-м Далее произведем расчет по формуле (2.23), а затем из условия (2.24) определим азат и из формулы (2.22) выразим и рассчитаем F3aт: 3800 ам = -j = 0,03 МПа 1 - 390 - 2300 6 азат = 2 - 0,03 = 0,06 МПа р _зазат • Аст _0,06 - 390 - 2300 _ F — — — 1 794 Н зат . z 30 Таким образом, была найдена необходимая сила затяжки болтов для нераскрытия стыка. Предварительная оценка стоимости конструкции Для создания прототипа беспилотного летательного аппарата для эвакуации людей из труднодоступных мест необходимо произвести закупку следующих основных изделий, приведенных в таблице 8. Таблица 8 - Основные покупные изделия
В итоге примерная стоимость составляет 1530000 €, что на сегодняшний курс составляет примерно 121 млн рублей.
3 Математическая модель Квадрокоптер - летательный аппарат, который имеет четыре несущих винта, где два противоположных винта вращаются в одном направлении, а два других - в обратном. Маневрирование осуществляется при помощи изменения скоростей вращения винтов. Необходимость создания математической модели обуславливается тем, что нужно как можно точнее описать управление летательным аппаратом. Квадрокоптер имеет шесть степеней свободы, но управлять можно только скоростями вращения винтов. Рассмотрим квадрокоптер (рис. 3.1) с известными физическими параметрами, который осуществляет движение относительно неподвижной инерциальной системы отсчета, связанной с Землей. Инерциальная система задана перпендикулярными координатными осями Ox,Oy,Oz , ось Oz направлена противоположно вектору силы тяжести. С квадрокоптером связана система координат, центр которой размещен в центре масс аппарата, а оси OxB,OyB,OzB параллельны и сонаправлены с осями неподвижной системы. Угловое положение аппарата задается тремя параметрами: углами крена ф, тангажа 0 и рыскания у, которые определяют вращение вокруг осей OxB,OyB,OzB . 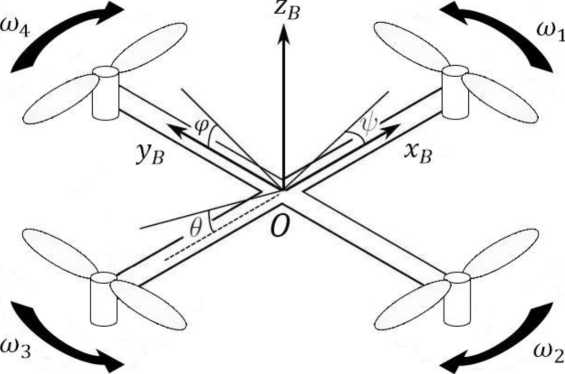 Рисунок 3.1 - Система координат квадрокоптера
Кинематические уравнения В полученной системе координат линейные скорости зададим вектором V , а угловые - v: vx,B    VB = v y,B (3.1)  v= (3.2) На рисунке 3.2 изображена схема ориентации квадрокоптера с помощью углов крена, тангажа и рыскания, которая позволяет составить матрицы поворота аппарата. 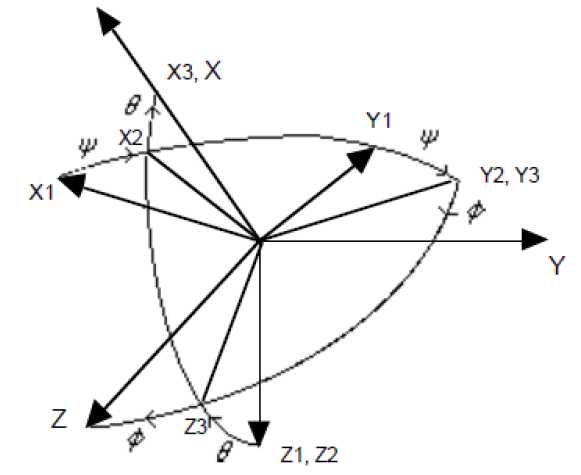  Рисунок 3.2 - Схема ориентации квадрокоптера в пространстве Матрицы поворота аппарата будут иметь следующие виды:
  
(3.4) (3.5) Объединим полученным матрицы и получим:      cos^ cos О sin^ cos О - sin щ cos ф + cos щ sin О sin ф cos щ cos ф + sin щ sin О sin ф - sin О Xi cos О sin ф Y1 (3.6)     sin щ sin ф + cos щ sin О cos ф - cos щ sin ф + sin щ sin О cos ф cos О cos ф Zi Матрица поворота является ортогональной, значит матрица поворота в подвижной системе будет находиться следующим образом R 1 = RT. Связь между линейными скоростями в инерциальной и подвижной системах координат задается следующим отношением: (3.7) Получаем следующие соотношения для угловых скоростей:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
