|
|
подготовка к цт. курсы мат. Ал Простейшие математические модели
Геом-1. Углы и прямые на плоскости
А1
|
ЦТ21Треугольник  - равнобедренный с основанием АВ. Используя данные рисунка, найдите градусную меру угла ВАС треугольника - равнобедренный с основанием АВ. Используя данные рисунка, найдите градусную меру угла ВАС треугольника 
|

|
|
1) 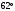 ; ;
2) 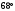 ; ;
3) 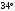 ; ;
4) 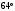 ; ;
5) 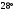 . .
|
А1.
|
ЦТ12 Укажите номер рисунка, на котором изображен равнобедренный треугольник:
 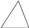    1) 2) 3) 4) 5) 1) 2) 3) 4) 5)
550 700 550 650 550 600 550 750 550 500
|
1) 1; 2) 2;
3) 3; 4) 4;
5) 5.
|
А2
|
ЦТ16 На рисунке изображен треугольник 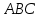 , в котором , в котором 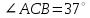 , , 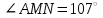 . Используя данные рисунка, найдите градусную меру угла . Используя данные рисунка, найдите градусную меру угла 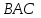 . .
|

|
|
1) 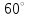 ; 2) ; 2) 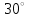 ; ;
3) 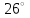 ; 4) ; 4) 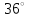 ; ;
5) 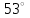 . .
|
А7
|
ЦТ20 На рисунке изображен треугольник 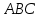 , в котором , в котором 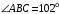 , , 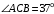 . Используя данные рисунка, найдите градусную меру угла . Используя данные рисунка, найдите градусную меру угла  четырехугольника четырехугольника
|
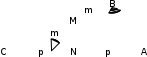
|
|
1)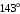 ; 2) ; 2)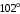 ; ;
3) 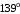 ; ;
4) 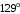 ; ;
5) 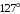 . .
|
А3
|
Д17 Используя данные рисунка, найдите градусную меру угла 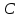 треугольника треугольника 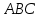 . .
|

A
x
4x
C B

|
|
1)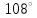 ;2) ;2)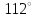 ; ;
3) 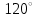 ; ;
4) 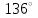 ; ;
5) 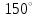 . .
|
А3.
|
ЦТ14Прямые  и и 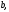 пересекаясь, образуют четыре угла. Известно, что сумма трех углов равна пересекаясь, образуют четыре угла. Известно, что сумма трех углов равна 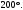 Найдите градусную меру меньшего угла. Найдите градусную меру меньшего угла.
|
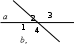
|
|
1) 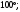 2) 2) 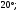
3) 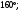
4) 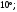
5) 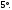
|
А6.
|
ЦТ13 На рисунке изображен развернутый угол  и лучи и лучи 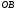 и и 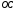 . Известно, что . Известно, что 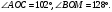 Найдите величину угла Найдите величину угла 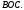
|

|
|
1) 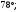 2) 2) 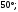
3) 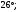 4) 4) 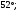
5) 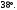
|

|
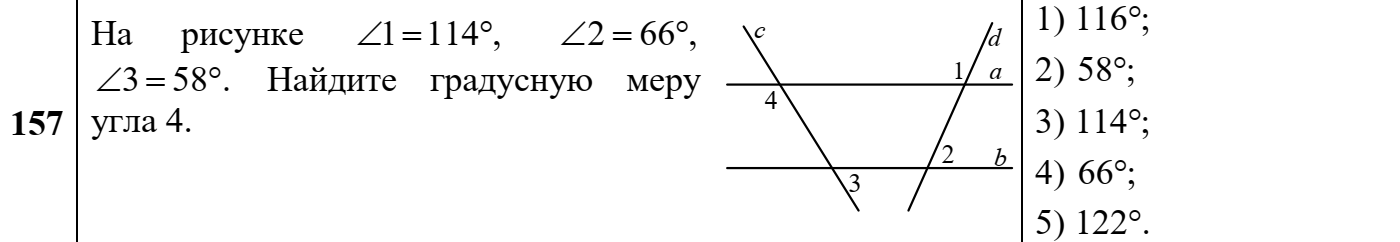
|
А7
|
ЦТ20 На рисунке  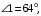 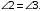 Найдите градусную меру угла 4. Найдите градусную меру угла 4.
|
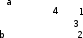
|
|
1) 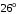 ; 2) ; 2) 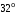 ; ;
3) 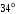 ; 4) ; 4) 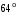 ; ;
5) 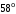 . .
|
А4
|
ЦТ18 Из вершины угла KMN, градусная мера которого равна 156, проведены два луча: MP, делящий данный угол пополам, и MF, делящий его в отношении 15:11. Найдите градусную меру угла FMP.
|
1) 6; 2) 10;
3) 12; 4) 26;
5) 24.
|
|
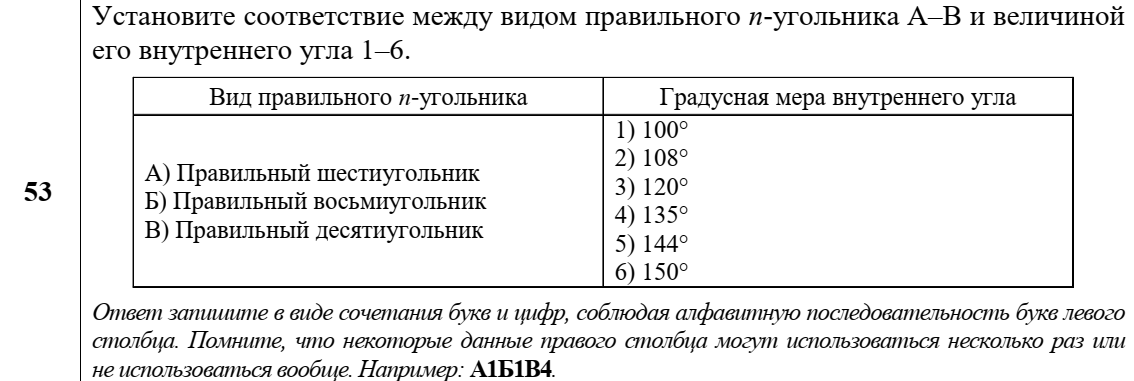
Геом-2. Прямоугольная система координат на плоскости. Расстояние между двумя точками. Уравнение окружности
А1.
|
ЦТ15 На координатной прямой отмечены точки O, A, B, C, D, F. Если
|
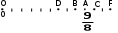
|
координата точки A равна 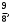 то числу 1 на координатной прямой соответствует точка: то числу 1 на координатной прямой соответствует точка:
|
1) B;
2) C;
3) D;
4) F;
5) O.
|
А1
|
ЦТ19 На координатной прямой отмечены точки A, B, C, D, F. Числу 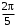 на координатной прямой может соответствовать точка: на координатной прямой может соответствовать точка:
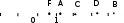
|
1) A;
2) B;
3) C;
4) D;
5) F.
|
А3
|
ЦТ18 На координатной прямой отмечены точки A, B, D, E. Укажите точки, координаты которых являются противоположными числами.
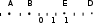
|
1) DиE;
2) BиE;
3) AиD;
4) BиD;
5) AиE.
|
А5
|
ЦТ20 Среди точекC(28), D(22), E(11), F(32), K(40) координатной прямой укажите точку, симметричную точке A(4) относительно точки B(18).
|
1)C(28);2) D(22);
3) E(11);4) F(32);
5) K(40).
|
А5
|
ЦТ20 На координатной прямой отмечены точки 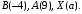 Найдите длину отрезка BX, если точки B и X симметричны относительно точки A. Найдите длину отрезка BX, если точки B и X симметричны относительно точки A.
|
1) 26; 2) 22;
3) 10; 4)13; 5) 32.
|
А6
|
ЦТ19 Окружность задана уравнением 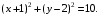 Укажите номер верного утверждения: Укажите номер верного утверждения:
1) Диаметр окружности равен 10;
2) прямая 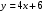 проходит через центр окружности; проходит через центр окружности;
3) радиус окружности равен 5;
4) точка 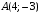 лежит на окружности; лежит на окружности;
5) центром окружности является точка 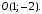
|
1) 1;
2) 2;
3) 3;
4) 4;
5) 5.
|
А7
|
ЦТ19 Точка A находится в узле сетки (см. рис.). Если точка B симметрична точке A относительно начала координат, то длина отрезка AB равна:
|
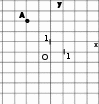
|

|
1) 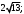
2) 6;
3) 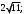
4) 4;
5) 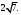
|
А9
|
ЦТ20 На координатной плоскости даны точки A и M, расположенные в узле сетки (см. рис.). Укажите координаты точки, симметричной точке A относительно точки M.
|
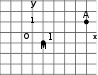
|
|
1) 
2) 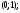
3) 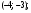
4) 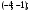
5) 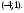
|
А9
|
ЦТ20 На координатной плоскости даны точка A, расположенная в узле сетки, и прямая l (см. рис.). Определите координаты точки, симметричной точке A относительно прямой l.
|
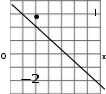
|
|
1) 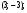
2) 
3) 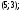
4) 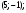
5) 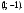
|
А10.
|
ЦТ13 Точки 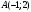 и и 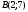 - вершины квадрата - вершины квадрата 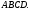 Периметр квадрата равен: Периметр квадрата равен:
|
1) 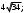 2) 2) 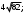
3)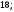 4) 4)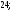 5) 5)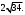
|
А17
|
ЦТ21Точки А и В расположены в узлах сетки (см.рис.) и являются соседними вершинами квадрата ABCD. Найдите площадь квадрата ABCD.
|     
1
1
B
A
|
|
1) 37;
2) 14;
3) 81;
4) 50;
5) 53.
|
А11
|
Д17 Окружность задана уравнением 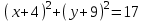 . Расстояние от центра окружности до точки . Расстояние от центра окружности до точки 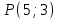 равно: равно:
|
1) 17; 2)15; 3) 13;
4) 12; 5) 9.
|
А16
|
ЦТ20 На одной стороне прямого угла O отмечены точки A и B так, что 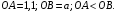 Составьте формулу, по которой можно вычислить радиус r окружности, проходящей через точки A, B и касающейся другой стороны угла. Составьте формулу, по которой можно вычислить радиус r окружности, проходящей через точки A, B и касающейся другой стороны угла.
|
1) 
2) 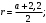
3) 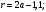
4) 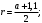
5) 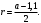
|
В3.
|
ЦТ12 Точки 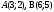 и и 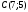 - вершины трапеции - вершины трапеции 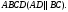 Найдите сумму координат точки Найдите сумму координат точки 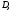 если если 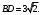
| |
|
|
 Скачать 2.09 Mb.
Скачать 2.09 Mb.