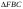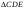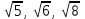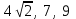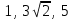|
|
подготовка к цт. курсы мат. Ал Простейшие математические модели
Алг-8. Иррациональные выражения. Модули
А5
|
ЦТ17 Значение выражения 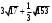 равно: равно:
|
1)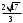 ; 2) ; 2)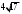 ; 3) ; 3)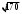 ; ;
4)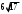 ; 5) ; 5)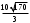 . .
|
А10
|
ЦТ18Значение выражения 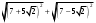 равно: равно:
|
1) 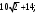 2) 2) 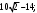
3) 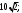 4) 14; 5) 4) 14; 5) 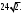
|
А12
|
ЦТ20 Значение выражения 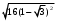 равно: равно:
|
1) 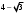 ; 2) ; 2) 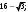 3) 3) 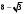 ; ;
4) 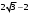 ; 5) ; 5) 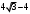 . .
|
А8
|
ЦТ21Результат упрощения выражения 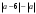 при при 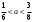 имеет вид: имеет вид:
|
1) -6; 2) 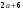 ; ;
3)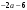 ; 4) ; 4) 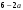 ; 5) 6. ; 5) 6.
|
А10
|
ЦТ17 Результат упрощения выражения 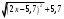 при при 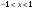 имеет вид: имеет вид:
|
1)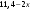 ; 2) ; 2)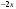 ; 3) ; 3)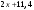 ; ;
4)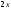 ; 5) ; 5)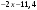 . .
|
А10
|
Д17 Результат упрощения выражения 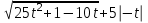 при при 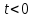 имеет вид: имеет вид:
|
1) 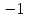 ; 2) ; 2) 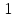 ; 3) ; 3) 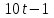 ; ;
4) 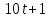 ; 5) ; 5) 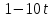 . .
|
А12
|
ЦТ20 Внесите множитель под знак корня в выражении 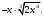
|
1) 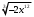 ; 2) ; 2) 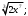 3) 3) 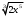 ; 4) ; 4) 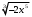 ; 5) ; 5) 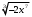 . .
|
А11.
|
ЦТ13 Упростите выражение 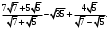
|
1)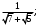 2) 2)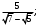
3) 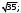 4) 4) 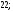 5) 5) 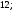
|
А17
|
ЦТ20 Расположите числа 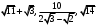 в порядке возрастания. в порядке возрастания.
|
1) 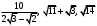 ; ;
2) 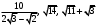 ; ;
3) 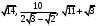 ; ;
4) 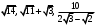 ; ;
5) 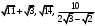 . .
|
В5
|
ЦТ16 Найдите значение выражения 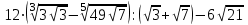 . .
|
Алг-9.Последовательности. Прогрессии
А6
|
Д17 Последовательность 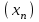 задается формулой: задается формулой: 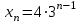 . Найдите разность . Найдите разность 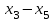 . .
|
1) 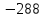 ; 2) ; 2) 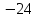 ; ;
3) 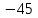 ; 4) ; 4) 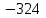 ; ;
5) 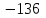 . .
|
А6
|
ЦТ17 Последовательность 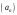 задана формулой задана формулой  -го члена -го члена 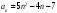 . Второй член этой последовательности равен: . Второй член этой последовательности равен:
|
1) 20; 2) 10;
3) 5; 4) 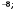
5) 8.
|
А11
|
ЦТ20 Последовательность 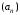 задана формулой n-го члена задана формулой n-го члена 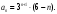 Найдите четвертый член этой последовательности. Найдите четвертый член этой последовательности.
|
1) 243; 2) 512; 3) 162;
4) 486; 5) 128.
|
А5
|
ЦТ16 Укажите формулу для нахождения 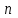 -го члена арифметической последовательности -го члена арифметической последовательности 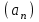 , если , если 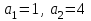 . .
|
1)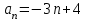 ;2) ;2) 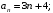
3) 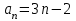 ; 4) ; 4) 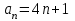 ; ;
5) 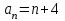 . .
|
А5
|
ЦТ18 Известно, что число 104 является членом арифметической прогрессии 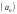 , заданной формулой , заданной формулой  -го члена -го члена 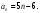 Найдите его номер. Найдите его номер.
|
1)15; 2)19;
3)20; 4)22;
5)24 .
|
А3.
|
ЦТ15Арифметическая прогрессия 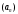 задана формулой n-го члена задана формулой n-го члена 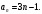 Найдите разность этой прогрессии. Найдите разность этой прогрессии.
|
1) 3; 2) 2; 3) 4;
4) -3; 5) -4.
|
А6.
|
ЦТ12 Число 185 является членом арифметической прогрессии 5, 9, 13, 17, … .Укажите его номер.
|
1) 51; 2) 43; 3) 45;
4) 46; 5) 49.
|
А11
|
ЦТ19 Сумма первых четырех членов геометрической прогрессии равна 90, знаменатель прогрессии равен 2. Найдите второй член геометрической прогрессии.
|
1) 24; 2) 6;
3) 8; 4) 12;
5) 15.
|
В1
|
ЦТ20 Дана арифметическая прогрессия (an), у которой 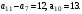 Для начала каждого из предложений Для начала каждого из предложений 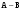 подберите его окончание 1 – 6 так, чтобы получилось верное утверждение. подберите его окончание 1 – 6 так, чтобы получилось верное утверждение.
Начало предложения
|
Окончание предложения
|
А) Разность этой прогрессии равна…
Б) Первый член этой прогрессии равен…
В) Сумма первых девяти членов этой прогрессии равна…
|
1) 3.
2) 4.
3) 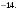
4) 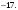
5) 2.
6) 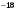 . .
|
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
|
В6.
|
ЦТ14Три числа составляют геометрическую прогрессию, в которой 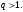 Если второй член прогрессии уменьшить на 12, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 49, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел. Если второй член прогрессии уменьшить на 12, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 49, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
|
В7.
|
ЦТ13 Геометрическая прогрессия со знаменателем 4 содержит 10 членов. Сумма всех членов прогрессии равна 30. Найдите сумму всех членов прогрессии с четными номерами.
|
В9
|
ЦТ2011 В арифметической прогрессии 80 членов, их сумма равна 80, а сумма членов с нечетными номерами на 160 больше суммы членов с четными номерами. Найдите тридцатый член этой прогрессии.
|
В11
|
ЦТ17 Первые члены арифметической и геометрической прогрессий одинаковы и равны 5,третьи члены также одинаковы, а вторые отличаются на 10. Найдите четвертый член арифметической прогрессии, если все члены обеих прогрессий положительны.
|
Геом4-5. Прямоугольный треугольник. Теорема Пифагора. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника
137
|
Длина гипотенузы прямоугольного треугольника равна 30, а косинус одного из острых углов равен 0,6. Найдите периметр треугольника.
|
1) 50; 2) 54; 3) 72;
4) 60; 5) 36.
|
А12
|
ЦТ19 В треугольнике ABC 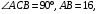 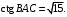 Найдите длину стороны CB. Найдите длину стороны CB.
|
1) 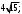 2) 2) 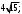 3) 4; 4) 5; 5) 3) 4; 4) 5; 5) 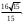
|
54
|
В треугольнике ABC: 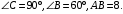 Найдите высоту CKэтого треугольника. Найдите высоту CKэтого треугольника.
|
1) 3; 2) 4; 3) 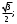
4) 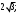 5) 5) 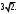
|
80
|
Найдите длину медианы, проведенной к гипотенузе прямоугольного треугольника с катетами, равными 4 и 6.
|
1) 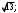 2) 2) 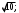 3) 5; 3) 5;
4) 26; 5) 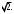
|
А13
|
ЦТ21Площадь прямоугольного треугольника равна 2, а радиус описанной около него окружности равен R. Укажите номер формулы, которой может выражаться сумма катетов а и b.
1) 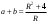 ; 2) ; 2) 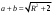 ; 3) ; 3) 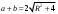 ; ;
4) 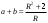 ; 5) ; 5) 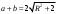 . .
|
1) 1; 2) 2;
3) 3; 4) 4;
5) 5.
|
74
|
Точка M лежит внутри угла A, равного 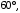 и находится на расстоянии и находится на расстоянии 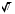 и и 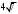 от его сторон. Найдите длину отрезка AM. от его сторон. Найдите длину отрезка AM.
|
Геом6. Произвольный треугольник
А12
|
ЦТ16 Длины всех сторон треугольника являются целыми числами. Если длина одной стороны треугольника равна 1, а другой – 10, то периметр треугольника равен:
|
1) 39; 2) 20; 3) 21;
4) 22; 5) 42.
|
А14
|
ЦТ19 В ботаническом саду разбили клумбу треугольной формы. Длина первой стороны клумбы равна 12 м, длина второй стороны в 2,5 раза больше длины первой, а длина третьей составляет не менее 120% от длины второй стороны Какому условию должен удовлетворять периметр P (в метрах) этой клумбы?
|
1) 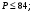 2) 2) 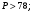
3) 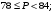
4) 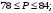
5) 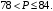
|
А14
|
ЦТ18 Длины двух сторон треугольника равны 6 и 8, его площадь равна 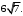 Найдите наибольшее значение, которое может принимать длина третьей стороны треугольника. Найдите наибольшее значение, которое может принимать длина третьей стороны треугольника.
|
1) 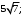 2) 2) 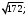
3) 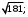 4) 13; 5) 14. 4) 13; 5) 14.
|
А14
|
ЦТ20 Диаметр окружности пересекает хорду под углом 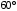 и точкой пересечения делит ее на отрезки длиной 3 и 5. Найдите квадрат радиуса окружности. и точкой пересечения делит ее на отрезки длиной 3 и 5. Найдите квадрат радиуса окружности.
|
1) 19; 2) 15; 3) 8;
4) 64; 5) 33.
|
163
|
Хорды AB и CD окружности пересекаются в точке M. Найдите косинус угла BMD, если AB = 16, CD = 19, BM = 6, 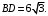
|
1) 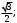 2) 2) 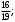
3) 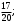 4) 4) 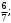 5) 5) 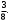
|
А12
|
ЦТ17 Определите остроугольный треугольник, зная длины его сторон (см. табл.).
Треугольник
|
Длины сторон треугольника
|
|
8 см; 15 см; 17 см
|
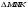
|
7 см; 13 см; 15 см
|
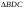
|
5 см; 6 см; 9 см
|
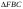
|
3 см; 4 см; 5 см
|
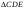
|
6 см; 7 см; 9 см
|
|
1) 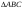 ; ;
2) 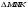 ; ;
3) 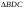 ; ;
4) 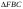 ; ;
5) 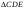 . .
|
В1
|
Д17 Установите соответствие между тройками чисел А-Д, которые являются длинами сторон треугольника, и видом треугольника 1-3.
Длины сторон треугольника
|
Вид треугольника
|
А) 3, 4, 5
Б) 2, 3, 4
В) 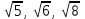
Г) 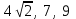
Д) 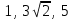
|
1) остроугольный
2) тупоугольный
3) прямоугольный
|
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последователь-ность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например, А1Б1В3Г2Д3
|
В3.
|
ЦТ13 Основание остроугольного равнобедренного треугольника равно 4, а синус противолежащего основанию угла равен 0,8. Найдите площадь треугольника.
|
В3.
|
ЦТ14В окружность радиусом 6 вписан треугольник, длины двух сторон которого равны 9 и 8. Найдите длину высоты треугольника, проведенной к его третьей стороне.
|
В12
|
ЦТ21Прямая, проходящая через вершину К треугольника KMN, делит его медиану МА в отношении 8:3, считая от вершины М, и пересекает сторону MN в точке В. Найдите площадь треугольника KMN, если площадь треугольника КМВ равна 16.
| |
|
|
 Скачать 2.09 Mb.
Скачать 2.09 Mb.
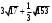 равно:
равно: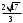 ; 2)
; 2)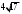 ; 3)
; 3)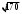 ;
;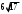 ; 5)
; 5)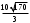 .
.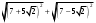 равно:
равно: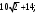 2)
2) 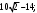
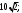 4) 14; 5)
4) 14; 5) 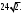
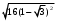 равно:
равно: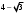 ; 2)
; 2) 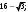 3)
3) 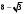 ;
; 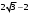 ; 5)
; 5) 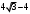 .
.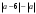 при
при 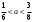 имеет вид:
имеет вид: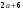 ;
;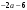 ; 4)
; 4) 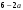 ; 5) 6.
; 5) 6.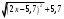 при
при 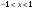 имеет вид:
имеет вид: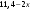 ; 2)
; 2)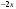 ; 3)
; 3)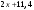 ;
;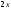 ; 5)
; 5)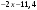 .
.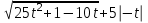 при
при 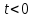 имеет вид:
имеет вид: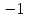 ; 2)
; 2) 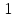 ; 3)
; 3) 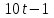 ;
;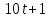 ; 5)
; 5) 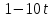 .
.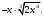
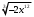 ; 2)
; 2) 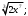 3)
3) 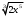 ; 4)
; 4) 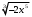 ; 5)
; 5) 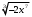 .
.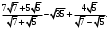
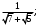 2)
2)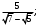
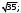 4)
4) 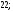 5)
5) 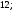
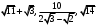 в порядке возрастания.
в порядке возрастания.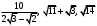 ;
; 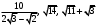 ;
;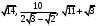 ;
; 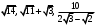 ;
;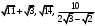 .
.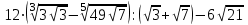 .
.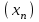 задается формулой:
задается формулой: 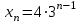 . Найдите разность
. Найдите разность 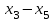 .
.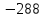 ; 2)
; 2) 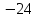 ;
;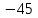 ; 4)
; 4) 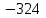 ;
;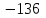 .
.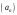 задана формулой
задана формулой  -го члена
-го члена 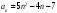 . Второй член этой последовательности равен:
. Второй член этой последовательности равен: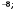
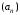 задана формулой
задана формулой 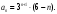 Найдите четвертый член этой последовательности.
Найдите четвертый член этой последовательности.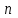 -го члена арифметической последовательности
-го члена арифметической последовательности 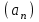 , если
, если 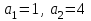 .
.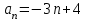 ;2)
;2) 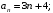
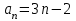 ; 4)
; 4) 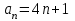 ;
;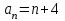 .
.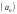 , заданной формулой
, заданной формулой 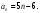 Найдите его номер.
Найдите его номер.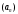 задана формулой n-го члена
задана формулой n-го члена 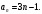 Найдите разность этой прогрессии.
Найдите разность этой прогрессии. 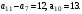 Для начала каждого из предложений
Для начала каждого из предложений 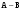 подберите его окончание 1 – 6 так, чтобы получилось верное утверждение.
подберите его окончание 1 – 6 так, чтобы получилось верное утверждение.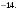
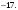
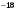 .
. 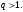 Если второй член прогрессии уменьшить на 12, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 49, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
Если второй член прогрессии уменьшить на 12, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 49, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.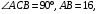
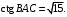 Найдите длину стороны CB.
Найдите длину стороны CB.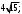 2)
2) 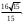
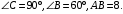 Найдите высоту CKэтого треугольника.
Найдите высоту CKэтого треугольника.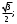
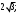 5)
5) 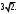
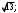 2)
2) 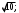 3) 5;
3) 5; 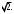
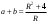 ; 2)
; 2) 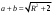 ; 3)
; 3) 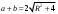 ;
; 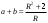 ; 5)
; 5) 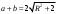 .
.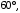 и находится на расстоянии
и находится на расстоянии 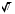 и
и 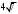 от его сторон. Найдите длину отрезка AM.
от его сторон. Найдите длину отрезка AM.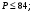 2)
2) 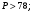
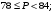
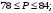
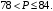
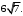 Найдите наибольшее значение, которое может принимать длина третьей стороны треугольника.
Найдите наибольшее значение, которое может принимать длина третьей стороны треугольника.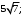 2)
2) 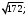
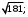 4) 13; 5) 14.
4) 13; 5) 14.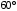 и точкой пересечения делит ее на отрезки длиной 3 и 5. Найдите квадрат радиуса окружности.
и точкой пересечения делит ее на отрезки длиной 3 и 5. Найдите квадрат радиуса окружности.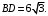
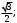 2)
2) 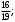
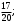 4)
4) 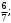 5)
5)