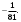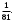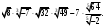|
|
подготовка к цт. курсы мат. Ал Простейшие математические модели
Алг-6.Одночлены и многочлены. Формулы сокращенного умножения
А8
|
ЦТ18 Для одночлена вида 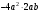 укажите номер верного утверждения. укажите номер верного утверждения.
1) Значение данного одночлена при 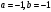 равно 8; равно 8;
2) Коэффициент данного одночлена равен 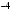 ; ;
3) Стандартным видом данного одночлена является одночлен 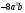 ; ;
4)Если данный одночлен разделить на 4, то получится 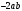 ; ;
5)Степень данного одночлена равна 3.
|
1) 1;
2) 2;
3) 3;
4) 4;
5) 5.
|
А5
|
ЦТ2011 Если 7 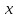 -17=0, то 14 -17=0, то 14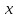 -39 равно: -39 равно:
|
1) 11 2) -9 3) -5 4) 5 5) 9
|
А4.
|
ЦТ14Результат разложения многочлена 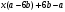 на множители имеет вид: на множители имеет вид:
|
1) 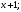 2) 2)  3) 3) 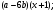
4) 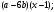 5) 5) 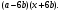
|
А5
|
ЦТ19 Результат разложения многочлена 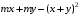 на множители имеет вид: на множители имеет вид:
|
1) 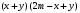 ; ;
2) 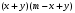 ; ;
3) 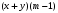 ; ;
4) 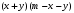 ; ;
5) 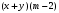 . .
|
А5.
|
ЦТ14Вычислите 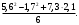
|
1) 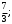 2) 2) 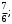 3) 7,3; 4) 3,86; 5) 7. 3) 7,3; 4) 3,86; 5) 7.
|
А9.
|
ЦТ15 Результат упрощения выражения 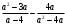 имеет вид: имеет вид:
|
1) 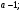 2) 2) 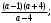 3) 3) 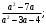
4) 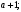 5) 5) 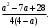
|
А12
|
ЦТ2011 Упростить выражение
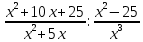
|
1) 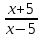 2) 2)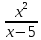 3) 3)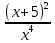 4) 4) 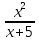 5) 5)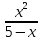
|
А13
|
ЦТ16 Сократите дробь 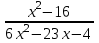 . .
|
1) 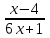 ; 2) ; 2) 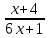 ; 3) ; 3) 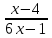 ; ;
4) 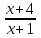 ; 5) ; 5) 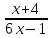 . .
|
А14.
|
ЦТ13 Упростите выражение 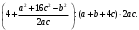
|
1) 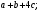 2) 2) 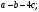 3) 4; 3) 4;
4) 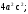 5) 5) 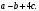
|
Геом-3. Окружность. Центральные и вписанные углы. Свойства касательных к окружности
А2
|
ЦТ20 Если вписанный угол DAB, изображенный на рисунке, равен 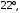 то вписанный угол DCB равен: то вписанный угол DCB равен:
|
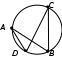
|
|
1) 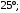
2) 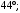
3) 
4) 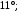
5) 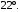
|

|

|

|
А2
|
ЦТ18 Две окружности с центрами A и B имеют одну общую точку C (см. рис.). Найдите радиус большей окружности, если радиус меньшей равен 3 и 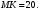
|
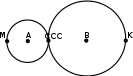
|
|
1) 7;
2) 9;
3) 10;
4) 14;
5) 6.
|
А9.
|
ЦТ12 Площадь круга равна 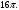 Диаметр этого круга равен: Диаметр этого круга равен:
|
1) 4; 2) 8; 3) 2
4) 4π; 5) 8π.
|
А7.
|
ЦТ15 Точки A, B, C разделили окружность так, что градусные меры дуг AB, BC и CA в указанном порядке находятся в отношении 9:5:4. Найдите градусную меру угла ABC.
|
1) 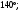 2) 2) 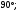 3) 3) 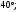 4) 4) 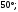 5) 5) 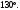
|
А8
|
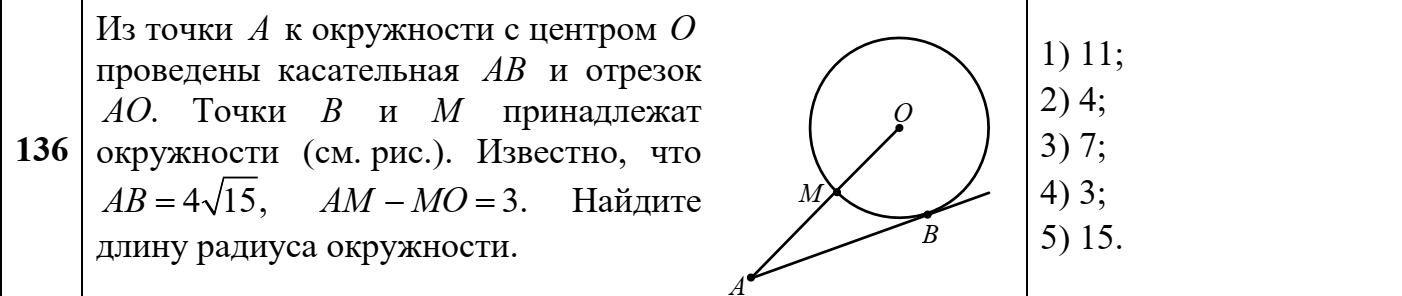
ЦТ19 Через точку  к окружности с центром в точке О проведены две касательные AB и АС, где B и С – точки касания (см. рис.). Найдите градусную меру угла ВАС, если к окружности с центром в точке О проведены две касательные AB и АС, где B и С – точки касания (см. рис.). Найдите градусную меру угла ВАС, если 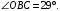
|
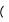   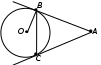
|
|
1) 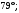
2) 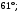
3) 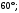
4) 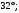
5) 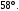
|
|
А10.
|
ЦТ14Из точки  к окружности проведены касательные AB и АС и секущая АМ, проходящая через центр окружности О. Точки В, С, М лежат на окружности (см. рис.). Известно, что к окружности проведены касательные AB и АС и секущая АМ, проходящая через центр окружности О. Точки В, С, М лежат на окружности (см. рис.). Известно, что 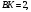 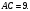 Найдите длину отрезка АК. Найдите длину отрезка АК.
|
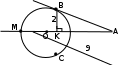
|
|
1) 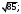
2) 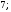
3) 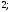
4) 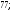
5) 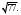
|
|

|
А13
|
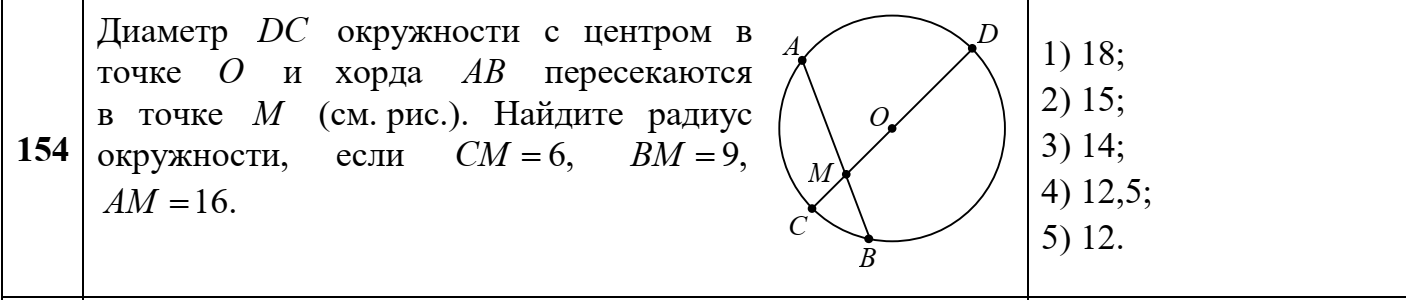
ЦТ20 В окружности радиуса 13 проведена хорда AB. Точка M делит хорду AB на отрезки длиной 9 и 16. Найдите расстояние от точки M до центра окружности.
|
1) 5;2) 4;3) 3; 4) 10; 5) 11.
|
В10.
|
ЦТ13 Из точки  проведены к окружности радиусом проведены к окружности радиусом 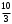 касательная касательная 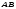 ( ( - точка касания) и секущая, проходящая через центр окружности и пересекающая ее в точках - точка касания) и секущая, проходящая через центр окружности и пересекающая ее в точках  и и 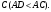 Найдите площадь Найдите площадь 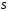 треугольника треугольника 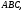 если длина отрезка если длина отрезка 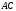 в 3 раза больше длины отрезка касательной. В ответ запишите значение выражения в 3 раза больше длины отрезка касательной. В ответ запишите значение выражения 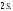 
|
Алг-7.Действия со степенями
А2.
|
ЦТ15 Запишите 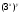 в виде степени с основанием 3. в виде степени с основанием 3.
|
1) 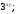 2) 2) 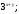 3) 3) 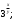
4) 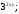 5) 5) 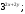
|
А3
|
ЦТ19 Укажите номер верного утверждения:
1) 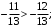 2) 2) 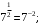 3) 3) 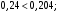
4) 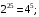 5) 5) 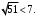
|
1) 1;
2) 2;
3) 3;
4) 4;
5) 5.
|
А6
|
ЦТ2011 Для любого числа 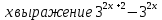 равно: равно:
|
1) 8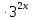 2) 6 3) 2) 6 3) 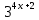
4) 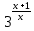 5) 9 5) 9
|
А9
|
ЦТ2011 Значение выражения 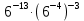 равно: равно:
|
1) 36 2) 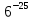 3) 6 3) 6
4) 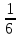 5) 5) 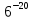
|
А4
|
ЦТ16 Значение выражения 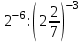 равно: равно:
|
1) 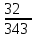 ; 2) ; 2) 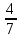 ; 3) ; 3) 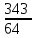 ; ;
4) 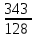 ; 5) ; 5) 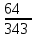 . .
|
А14.
|
ЦТ12 Упростить выражение 
|
1) 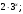 2) 2) 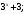
3) 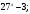 4) 4) 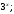 5) 5) 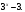
|
А15.
|
ЦТ12 Корень уравнения 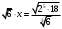 равен: равен:
|
1)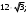 2) 2)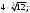 3) 3) 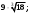 4) 4)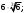 5) 5) 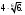
|
А10.
|
ЦТ15 Значение выражения 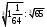 равно: равно:
|
1) 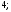 2) 2) 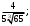 3) 3) 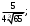
4) 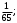 5) 5) 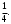
|
А16.
|
ЦТ14Расположите числа 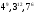 в порядке возрастания. в порядке возрастания.
|
1) 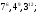 2) 2) 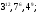
3) 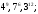 4) 4) 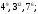
5) 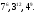
|
А17
|
ЦТ2011 Расположите числа 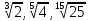 в порядке возрастания. в порядке возрастания.
|
1) 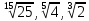 2) 2) 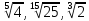
3) 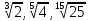 4) 4) 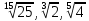
5) 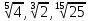
|
В1
|
ЦТ19 Для начала каждого из предложений 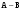 подберите его окончание 1 – 5 так, чтобы получилось верное утверждение. подберите его окончание 1 – 5 так, чтобы получилось верное утверждение.
Начало предложения
|
Окончание предложения
|
А) Значение выражения 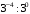 равно: равно:
Б) Значение выражения 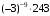 равно: равно:
В) Значение выражения 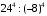 равно: равно:
|
1) 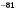 . .
2) 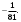
3) 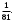
4) 27.
5) 81.
|
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
|
В5
|
ЦТ21 Найдите значение выражения 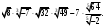
| |
|
|
 Скачать 2.09 Mb.
Скачать 2.09 Mb.
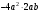 укажите номер верного утверждения.
укажите номер верного утверждения.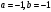 равно 8;
равно 8;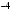 ;
;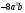 ;
;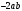 ;
;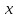 -17=0, то 14
-17=0, то 14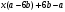 на множители имеет вид:
на множители имеет вид: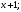 2)
2)  3)
3) 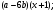
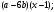 5)
5) 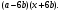
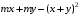 на множители имеет вид:
на множители имеет вид: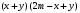 ;
;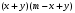 ;
;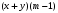 ;
;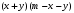 ;
;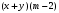 .
.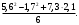
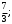 2)
2) 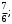 3) 7,3; 4) 3,86; 5) 7.
3) 7,3; 4) 3,86; 5) 7.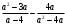 имеет вид:
имеет вид: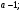 2)
2) 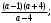 3)
3) 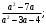
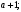 5)
5) 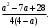
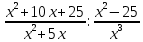
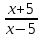 2)
2)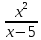 3)
3)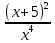 4)
4) 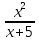 5)
5)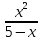
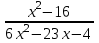 .
.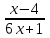 ; 2)
; 2) 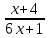 ; 3)
; 3) 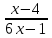 ;
; 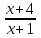 ; 5)
; 5) 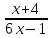 .
.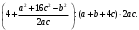
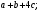 2)
2) 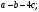 3) 4;
3) 4;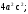 5)
5) 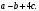
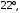 то вписанный угол DCB равен:
то вписанный угол DCB равен: 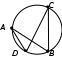
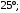
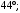

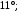
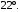



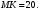
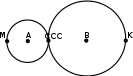
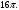 Диаметр этого круга равен:
Диаметр этого круга равен: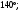 2)
2) 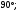 3)
3) 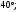 4)
4) 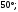 5)
5) 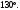
 к окружности с центром в точке О проведены две касательные AB и АС, где B и С – точки касания (см. рис.). Найдите градусную меру угла ВАС, если
к окружности с центром в точке О проведены две касательные AB и АС, где B и С – точки касания (см. рис.). Найдите градусную меру угла ВАС, если 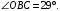
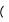



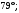
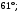
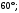
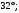
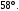

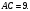 Найдите длину отрезка АК.
Найдите длину отрезка АК.
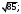
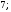
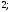
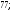
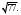


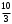 касательная
касательная 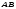 (
( - точка касания) и секущая, проходящая через центр окружности и пересекающая ее в точках
- точка касания) и секущая, проходящая через центр окружности и пересекающая ее в точках  и
и 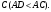 Найдите площадь
Найдите площадь 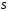 треугольника
треугольника 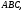 если длина отрезка
если длина отрезка 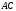 в 3 раза больше длины отрезка касательной. В ответ запишите значение выражения
в 3 раза больше длины отрезка касательной. В ответ запишите значение выражения 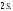

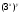 в виде степени с основанием 3.
в виде степени с основанием 3.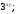 2)
2) 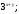 3)
3) 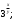
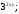 5)
5) 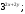
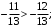 2)
2) 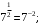 3)
3) 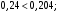
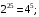 5)
5) 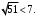
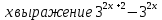 равно:
равно: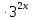 2) 6 3)
2) 6 3) 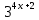
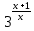 5) 9
5) 9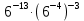 равно:
равно: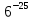 3) 6
3) 6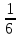 5)
5) 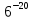
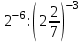 равно:
равно: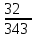 ; 2)
; 2) 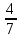 ; 3)
; 3) 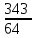 ;
;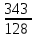 ; 5)
; 5) 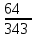 .
.
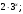 2)
2) 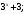
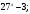 4)
4) 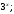 5)
5) 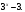
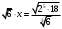 равен:
равен: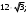 2)
2)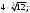 3)
3) 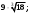 4)
4)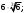 5)
5) 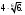
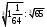 равно:
равно: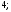 2)
2) 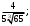 3)
3) 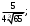
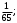 5)
5) 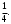
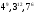 в порядке возрастания.
в порядке возрастания.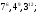 2)
2) 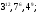
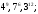 4)
4) 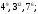
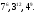
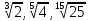 в порядке возрастания.
в порядке возрастания. 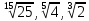 2)
2) 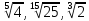
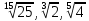
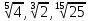
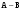 подберите его окончание 1 – 5 так, чтобы получилось верное утверждение.
подберите его окончание 1 – 5 так, чтобы получилось верное утверждение.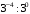 равно:
равно: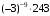 равно:
равно: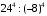 равно:
равно: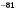 .
.