Глава. Глава 3. Аналитическая геометрия
 Скачать 1.38 Mb.
|
|
Теорема. Левая часть нормального уравнения (3.11) прямой L равна отклонению точки M с координатами  от прямой L , если координаты этой точки подставить в левую часть этого уравнения, т.е.: Доказательство. Спроектируем точку M на луч, определяемый единичным вектором  . Тогда  .Но  . Отсюда получаем, что . При этом расстояние от точки до прямой равно модулю отклонения, т.е.  . Для приведения общего уравнения прямой к нормальному виду поступим следующим образом. Уравнение  и  определяют одну и ту же прямую. Умножим первое из них на некоторый множитель t. Тогда  ,  ,  , откуда  и  . Знак у множителя t выбирается так, чтобы выполнялось условие  (расстояние всегда положительное), т.е. выбирается знак, противоположный знаку C ( ). Тогда отклонение какой-либо точки  от прямой определяется как  . (3.15)Расстояние от этой точки до прямой есть  .3.2. ЗАДАЧИ 1. Для прямой, заданной уравнением с угловым коэффициентом  :а) выписать угловой коэффициент; определить, острый или тупой угол образует прямая с положительным направлением оси  ;б) записать уравнение в общем виде; выписать координаты вектора нормали; в) записать уравнение в отрезках; нарисовать прямую; г) записать уравнение в каноническом виде; выписать два различных направляющих вектора; д) записать уравнение в параметрическом виде. 2. Даны:  ,  ,  ,  ,  . Записать и привести к общему виду:а) уравнение прямой с вектором нормали  , проходящей через точку  ;б) уравнение прямой, проходящей через точку  перпендикулярно направлению  ;в) уравнение прямой с направляющим вектором  , проходящей через точку ;г) уравнение прямой, проходящей через точки и  .3. Определить взаимное расположение прямых (пересекаются, параллельны, совпадают). Если прямые пересекаются, то найти точку пересечения и угол между ними; если прямые параллельны, то найти расстояние между ними: а)  ,  ;б) 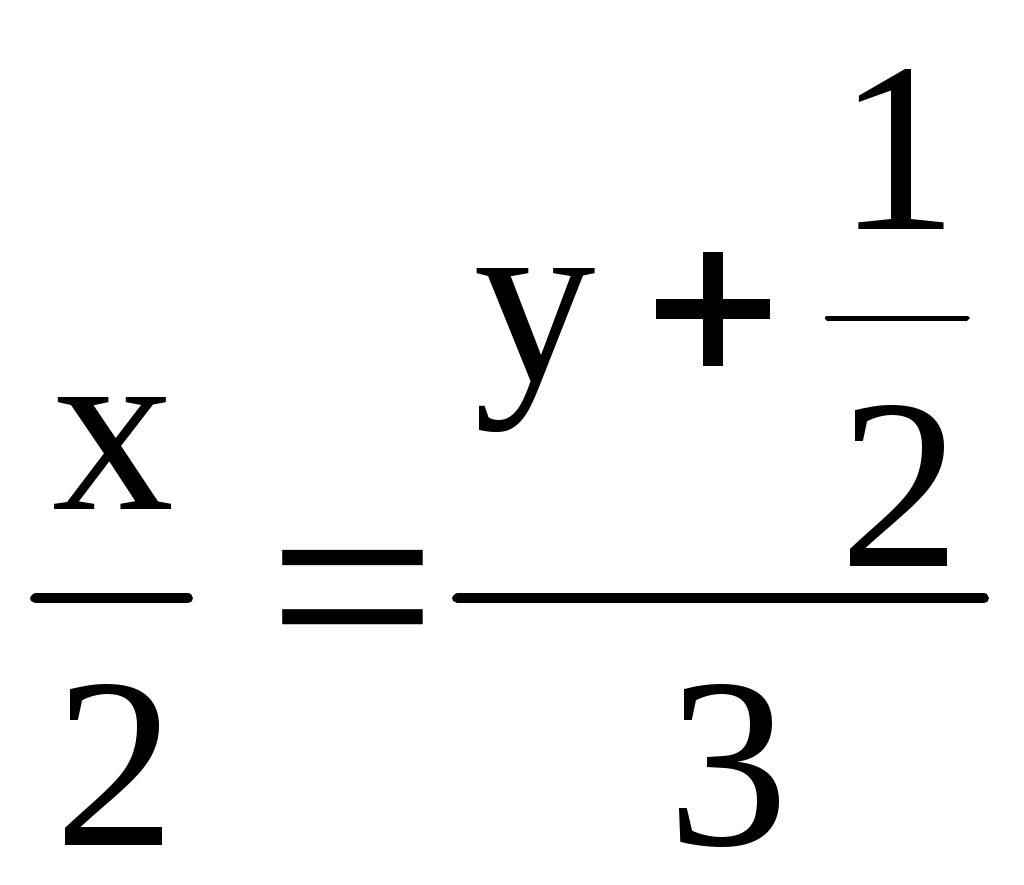 ,  ; в)  ,  .4. Определить, при каких значениях  и  две прямые  ,  : 1) параллельны; 2) совпадают; 3) перпендикулярны. 5. Дана прямая  . Составить уравнение прямой, проходящей через точку  : а) параллельно данной прямой; б) перпендикулярно к данной прямой. 6. Даны уравнения двух сторон прямоугольника  ,  и одна из его вершин А(2;-3). Составить уравнения двух других сторон этого прямоугольника.7. Даны вершины треугольника  ,  ,  . Составить уравнения его высот и биссектрисы внутреннего угла при вершине .8. Найти точку симметричную точке  относительно прямой  .Домашнее задание. 9. Прямая задана уравнением в общем виде  . Записать уравнение этой прямой в разных видах:а) уравнение с угловым коэффициентом; б) уравнение в отрезках; в) уравнение в каноническом виде; г) уравнение в параметрическом виде. 10. Даны:  ,  ,  ,  ,  . Записать и привести к общему виду:а) уравнение прямой с вектором нормали , проходящей через точку ;б) уравнение прямой, проходящей через точку перпендикулярно направлению ;в) уравнение прямой с направляющим вектором , проходящей через точку ;г) уравнение прямой, проходящей через точки и .11. Определить взаимное расположение прямых (пересекаются, параллельны, совпадают). Если прямые пересекаются, то найти точку пересечения и угол между ними; если прямые параллельны, то найти расстояние между ними: а)  ,  ;б) 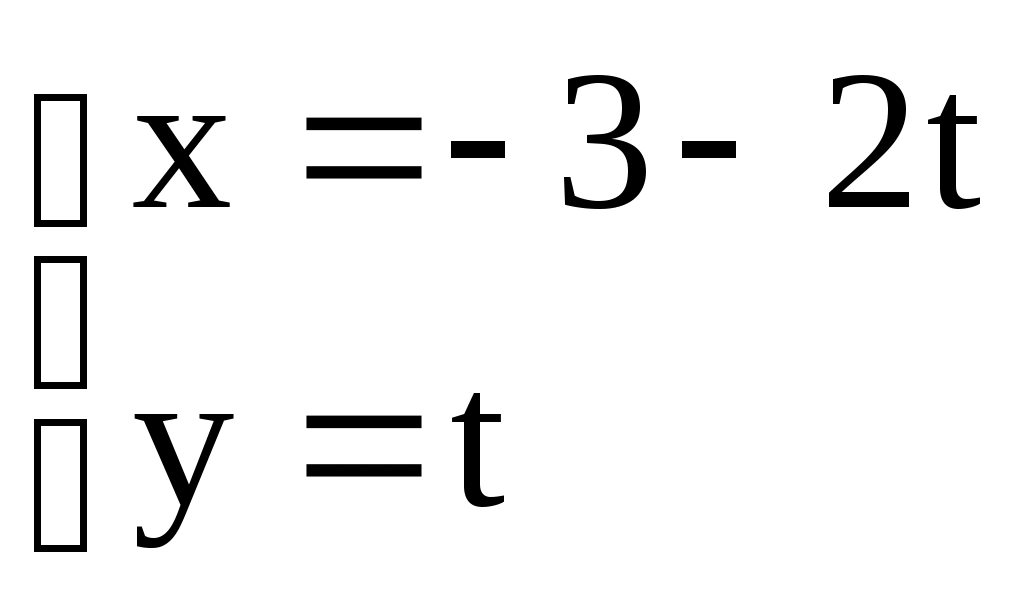 ,  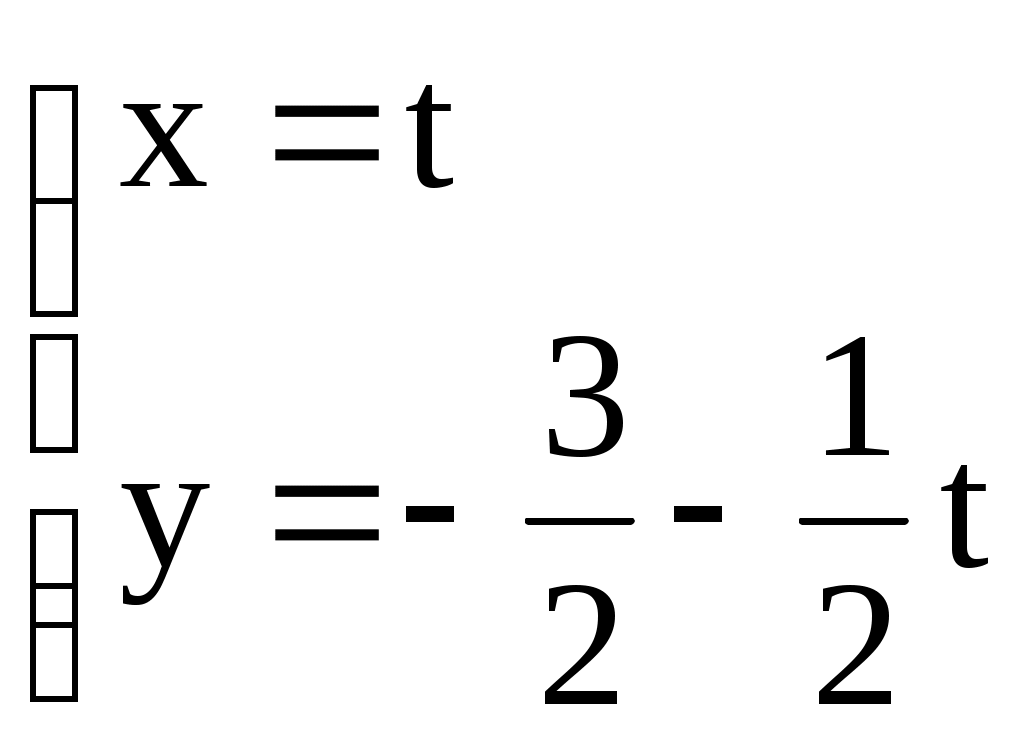; в)  ,  .12. Составить уравнения прямых, проходящих через вершины треугольника А(5;-4), В(-1;3), С(-3;-2) параллельно противоположным сторонам. 13. Даны стороны трапеции  ,  . Найти длину ее высоты.14.  ,  - стороны параллелограмма.  - одна из диагоналей. Найти координаты вершин.Ответы. 1. а) k = 2, острый; б) 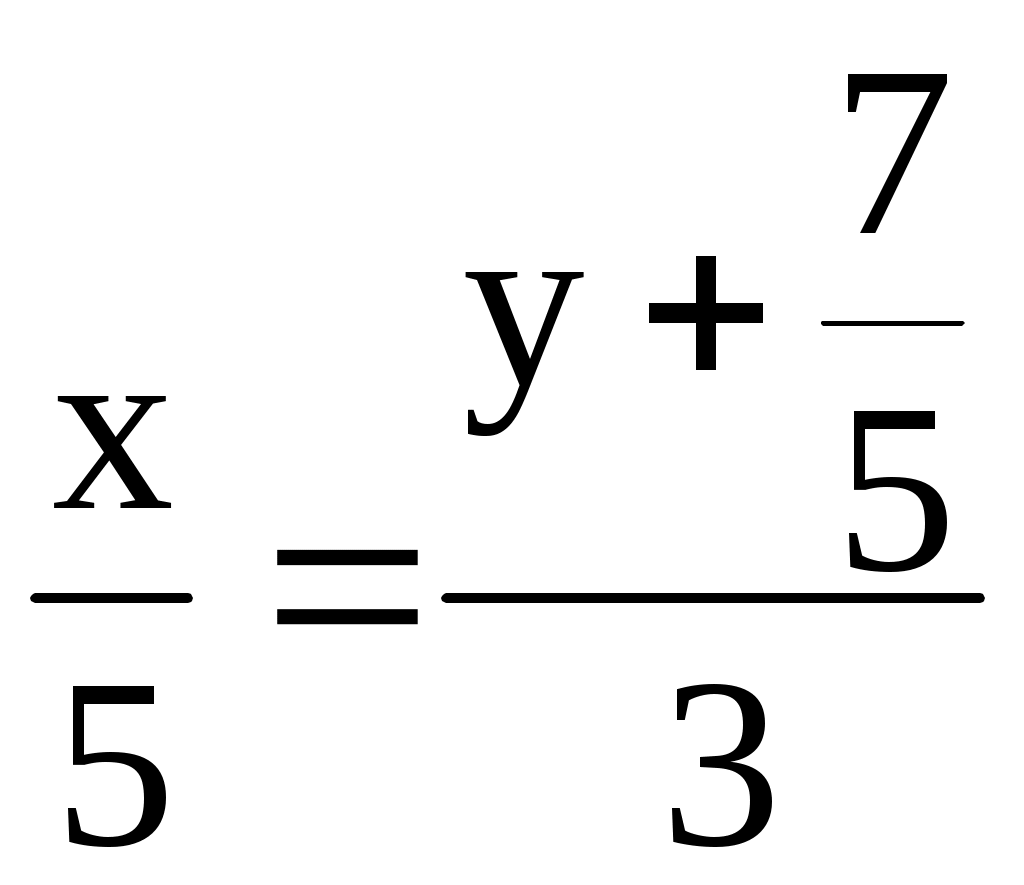 ,  ; в)  ; г)  ; д)  . 2. а)  ; б)  ; в)  ; г)  . 3. а) Пересекаются, (5;6),  ; б) совпадают; в) параллельны,  . 4. 1)  ,  или ,  ; 2)  ,  или ,  ; 3)  ,  . 5. а)  ; б)  . 6.  ,  . 7.  ,  ,  ,  . 8. (11;-11). 9. а)  ; б)  ; в)  ; г)  . 10. а)  ; б)  ; в)  ; г)  . 11. а) Параллельны,  ; б) Пересекаются,  ,  ; в) Совпадают. 12.  ,  ,  . 13.  . 14. (2;-2), (-2;0), (-2;2), (-6;4.)3.3. Плоскость в пространстве В пространстве с декартовой системой координат OXYZ выберем произвольную фиксированную точку  , произвольный фиксированный вектор  и произвольную точку пространства  . Составим скалярное произведение векторов ,  и приравняем его нулю. Тогда геометрическое место концов множества векторов  , удовлетворяющих этому уравнению, образует плоскость, перпендикулярную вектору и уравнение  . (3.16)есть векторное уравнение плоскости. Вектор называется нормальным вектором плоскости. В декартовых координатах уравнение (3.16) принимает вид  (3.17)и называется уравнением плоскости, проходящей через точку  с нормальным вектором . Если раскрыть скобки, то уравнение (3.17) можно записать как  , (3.18)где  - константа. Уравнение (3.18) называется общим уравнением плоскости. Оно называется полным уравнением плоскости, если  и неполным в противном случае. Полное уравнение плоскости можно привести к виду  или  , (3.19)где a, b, с – отрезки, отсекаемые плоскостью на осях OX, OY, OZ и такое уравнение называется уравнением плоскости в отрезках. Рассмотрим другой способ задания плоскости – с помощью двух направляющих векторов. Пусть заданы два неколлинеарных ненулевых вектора  и  . Выберем, как и ранее, произвольную фиксированную точку , произвольную точку  и построим вектор . Тогда равенство нулю смешанного произведения  (3.20)определяет плоскость, проходящую через точку параллельно плоскости, в которой лежат векторы  и  . Поэтому уравнение (3.20) называется уравнением плоскости в векторном виде. Его также можно записать через радиус-векторы точек и M:  . (3.21)В декартовых координатах это уравнение может быть записано  . (3.22)Раскрыв этот определитель, получим общее уравнение плоскости (3.18). С другой стороны, равенство нулю определителя означает, что его первая строка является линейной комбинацией остальных двух строк (вторая и третья строки линейно независимы как координаты неколлинеарных векторов) и тогда уравнение плоскости можно записать в виде следующей системы  , (3.23)где  - произвольные параметры и называется уравнением плоскости в параметрическом виде. В векторном виде система (3.23) может быть записана следующим образом . (3.24)Заметим, что между нормальным вектором плоскости  е ее направляющими векторами  и  существует простая связь:  . |