Глава. Глава 3. Аналитическая геометрия
 Скачать 1.38 Mb. Скачать 1.38 Mb.
|
|
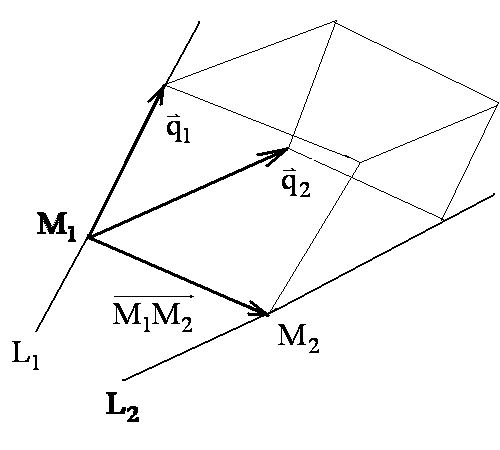
3.5.1. Угол между прямыми в пространстве. Угол между двумя прямыми определяется углом между направляющими векторами этих прямых: \ 3.5.2. Некоторые типовые задачи. 1. Угол между прямой и плоскостью. Рассмотрим плоскость Условие параллельности прямой и плоскости: 2. Условие принадлежности прямой 3. Условие принадлежности двух прямых одной плоскости. Две прямые 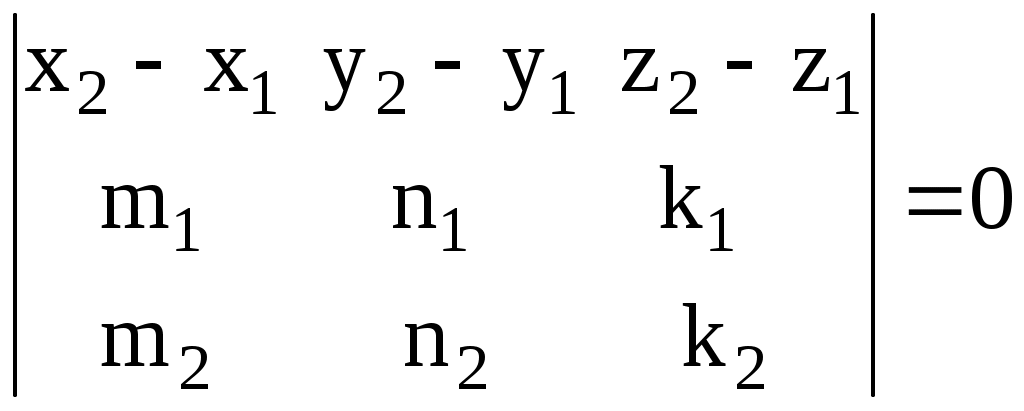 . Если данный определитель не равен нулю, то прямые не пересекаются и не параллельны. Такие прямые называются скрещивающимися прямыми. . Если данный определитель не равен нулю, то прямые не пересекаются и не параллельны. Такие прямые называются скрещивающимися прямыми.4. Условие пересечения трех плоскостей. Точка пересечения плоскостей находится из решения системы уравнений 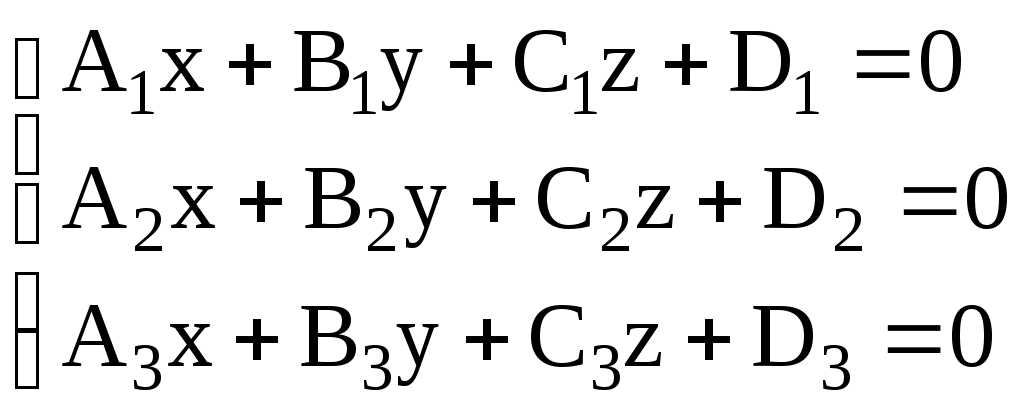 Необходимым и достаточным условием ее существования является отличие от нуля определителя этой системы. В противном случае они либо пересекаются по прямой, если ранг матрицы системы равен двум, либо они параллельны, если ранг матрицы равен единице. Необходимым и достаточным условием ее существования является отличие от нуля определителя этой системы. В противном случае они либо пересекаются по прямой, если ранг матрицы системы равен двум, либо они параллельны, если ранг матрицы равен единице.5. Пересечение прямой и плоскости. Чтобы найти точку пересечения плоскости 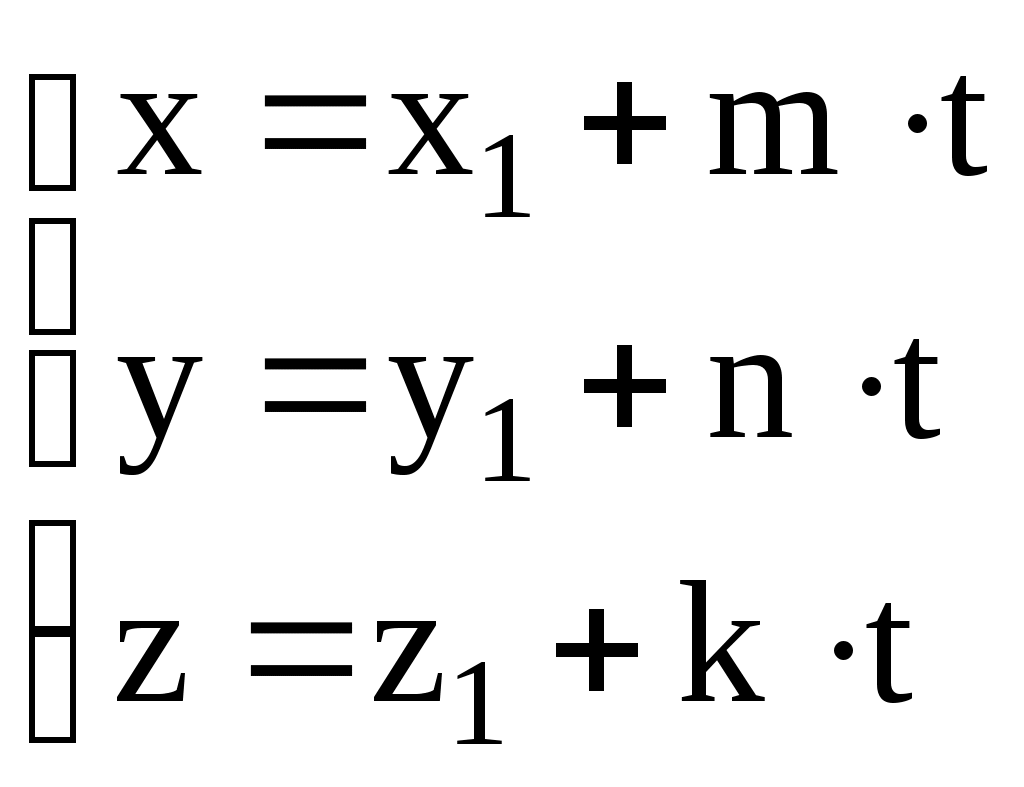 , подставить полученные выражения для координат в уравнение плоскости и найти значение параметра t. Подставив это найденное значение параметра в выражения для координат, найдем искомые значения координаты точки пересечения. , подставить полученные выражения для координат в уравнение плоскости и найти значение параметра t. Подставив это найденное значение параметра в выражения для координат, найдем искомые значения координаты точки пересечения.6. Уравнение прямой, проходящей через точку Здесь достаточно в качестве направляющего вектора прямой взять нормальный вектор данной плоскости 7. Уравнение плоскости, проходящей через точку В этом случае искомая плоскость имеет тот же нормальный вектор 8. Уравнение плоскости, проходящей через точку В этом случае в качестве нормального вектора плоскости следует выбрать направляющий вектор прямой: 9. Расстояние от точки Существует два способа. Первый способ. 1). Составляется уравнение плоскости, проходящей через точку 10. Уравнение перпендикуляра, опущенного из заданной точки Через точку 11. Определение расстояния между скрещивающимися прямыми. Расстояние между скрещивающимися прямыми
3.6. ЗАДАЧИ 1. Написать канонические уравнения прямой, проходящей через точку а) вектору в) оси 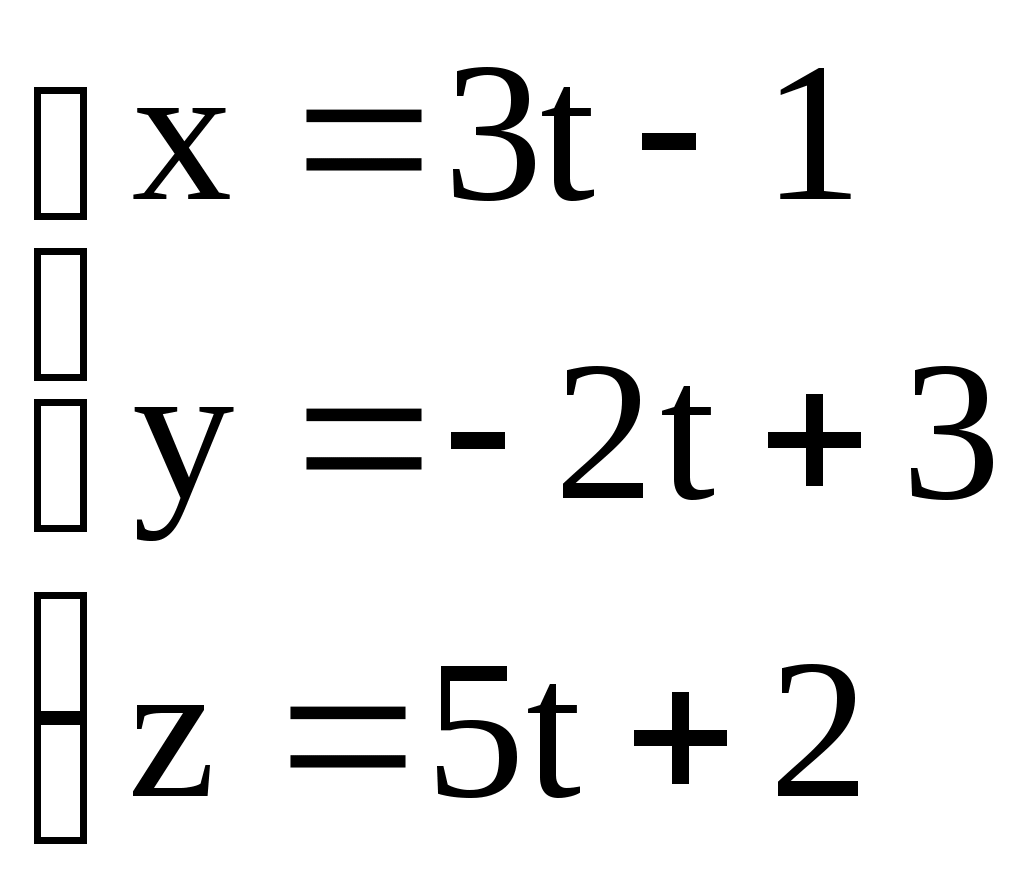 . .2. Составить канонические и параметрические уравнения прямой, проходящей через точки 3. Составить параметрические уравнения прямой 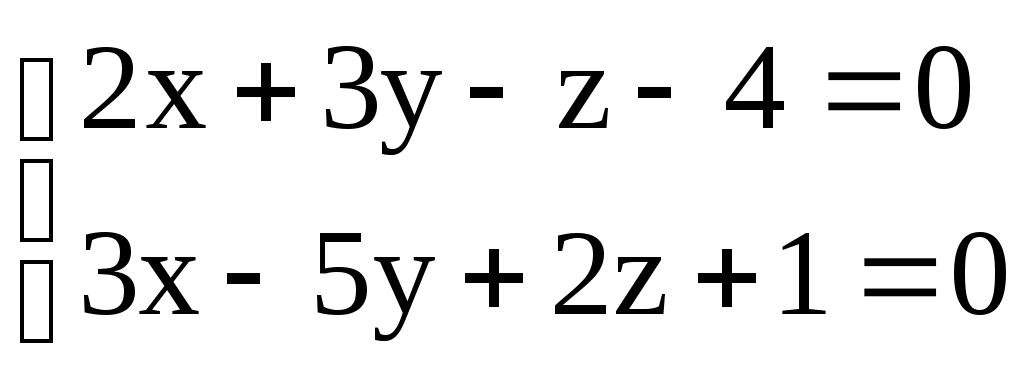 . .4. Написать канонические уравнения прямой, проходящей через точку 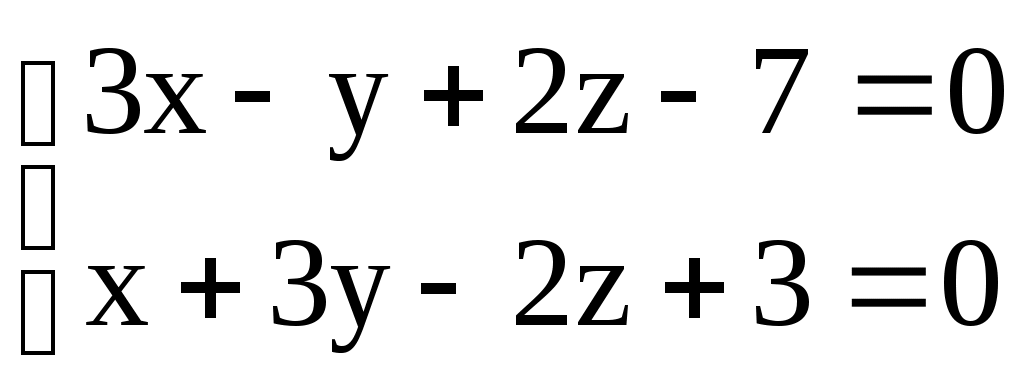 . .5. Определить взаимное расположение прямой и плоскости (пересекаются, параллельны, прямая лежит в плоскости). Если прямая и плоскость пересекаются, то найти точку пересечения и угол между ними; если параллельны, то найти расстояние между ними: а) 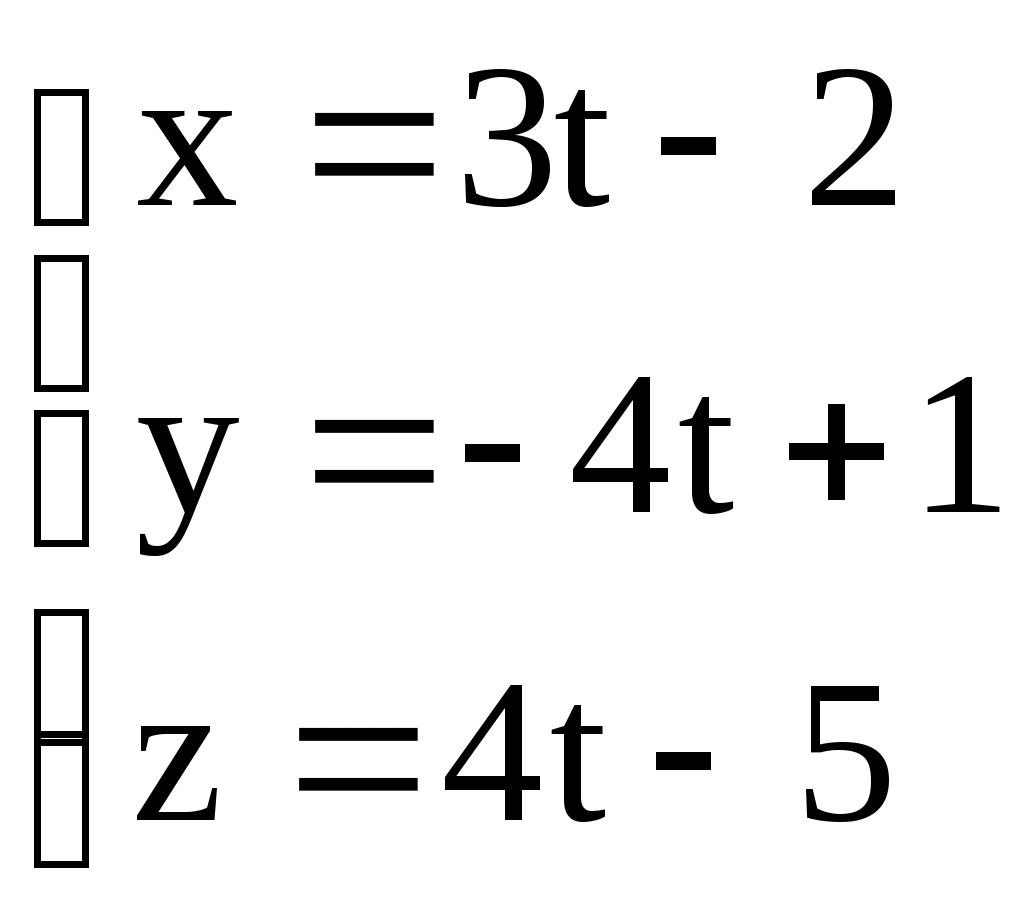 , , б) в) 6. Составить уравнение плоскости, проходящей через точку а) перпендикулярно к прямой б) проходящей через прямую 7. Найти расстояние от точки М(-25;7;10) до прямой 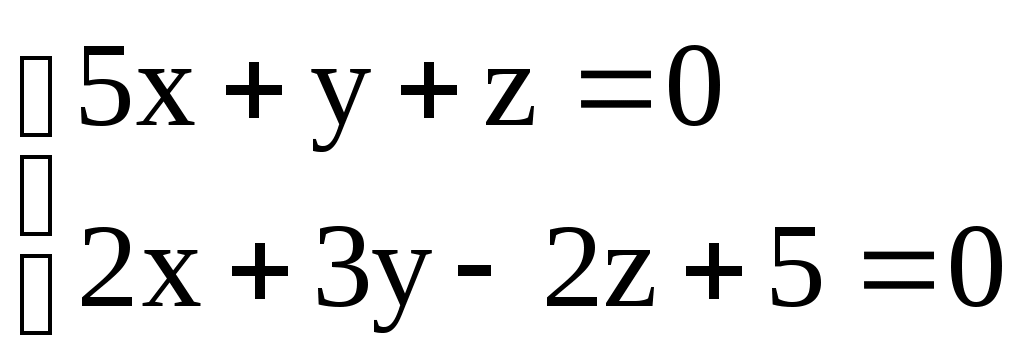 . .8. Найти точку N, симметричную точке М(1;3;-4) относительно плоскости Домашнее задание. 9. Составить канонические и параметрические уравнения прямой, проходящей через точки 10. Составить параметрические уравнения прямой 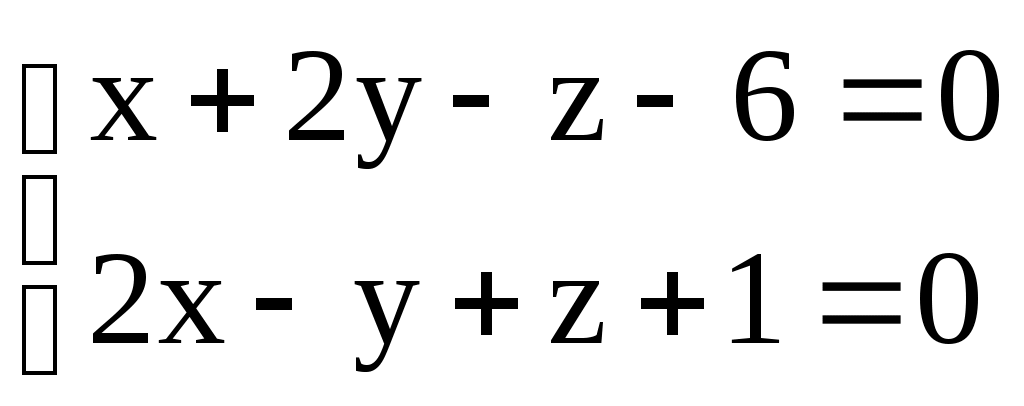 . .11. Составить уравнение прямой, проходящей через точку 12. Даны вершины треугольника А(3;6;-7), В(-5;2;3), С(4;-7;-2). Составить параметрические уравнения его медианы, проведенной из вершины С. 13. Определить взаимное расположение прямой и плоскости (пересекаются, параллельны, прямая лежит в плоскости). Если прямая и плоскость пересекаются, то найти точку пересечения и угол между ними; если параллельны, то найти расстояние между ними: а)  , , б) в) 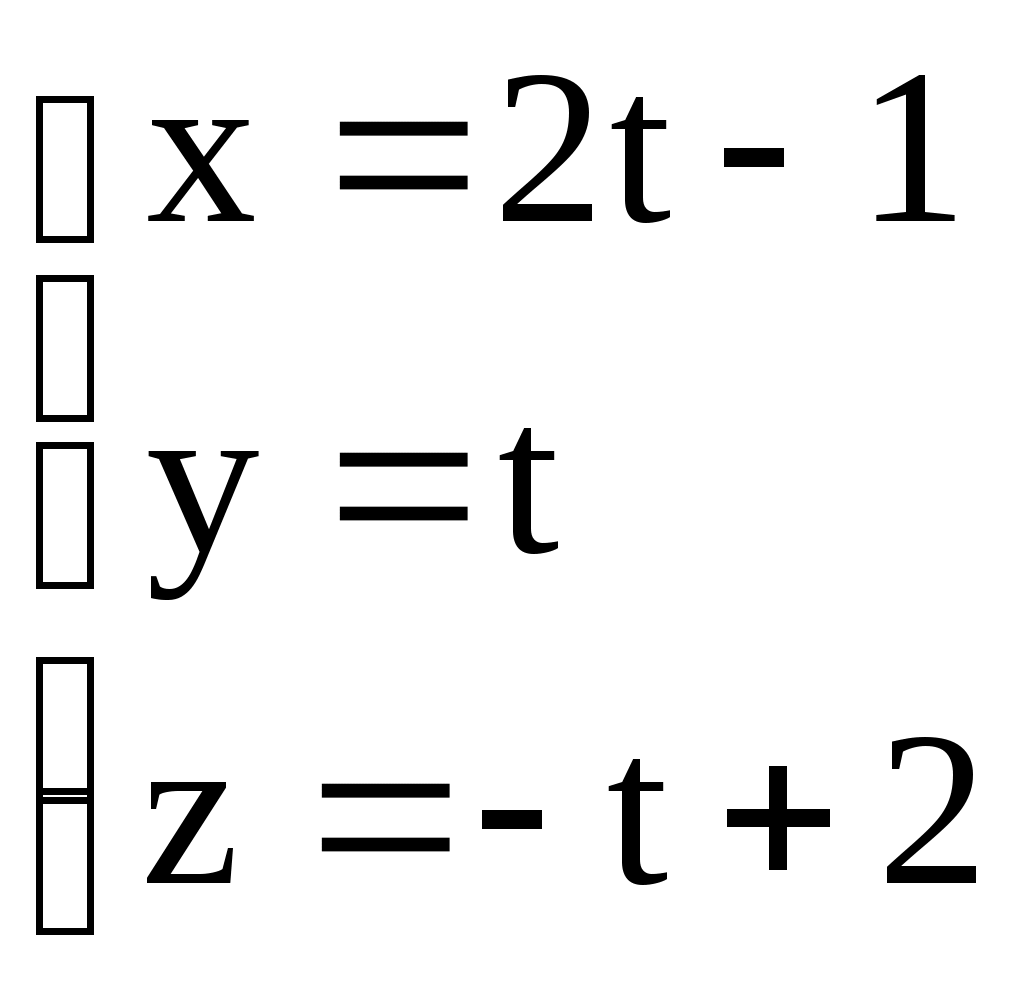 , , 14. Составить уравнение плоскости, проходящей через точку Ответы. 1. а) г) 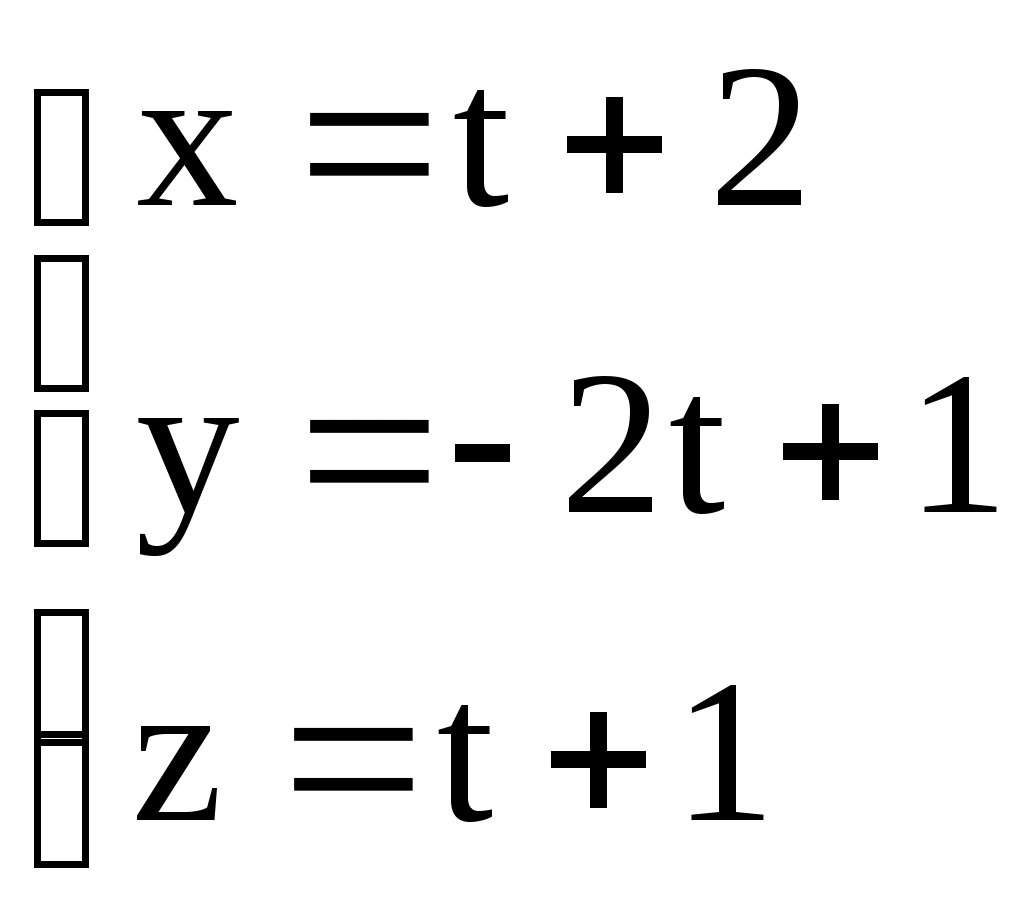 . . 3. 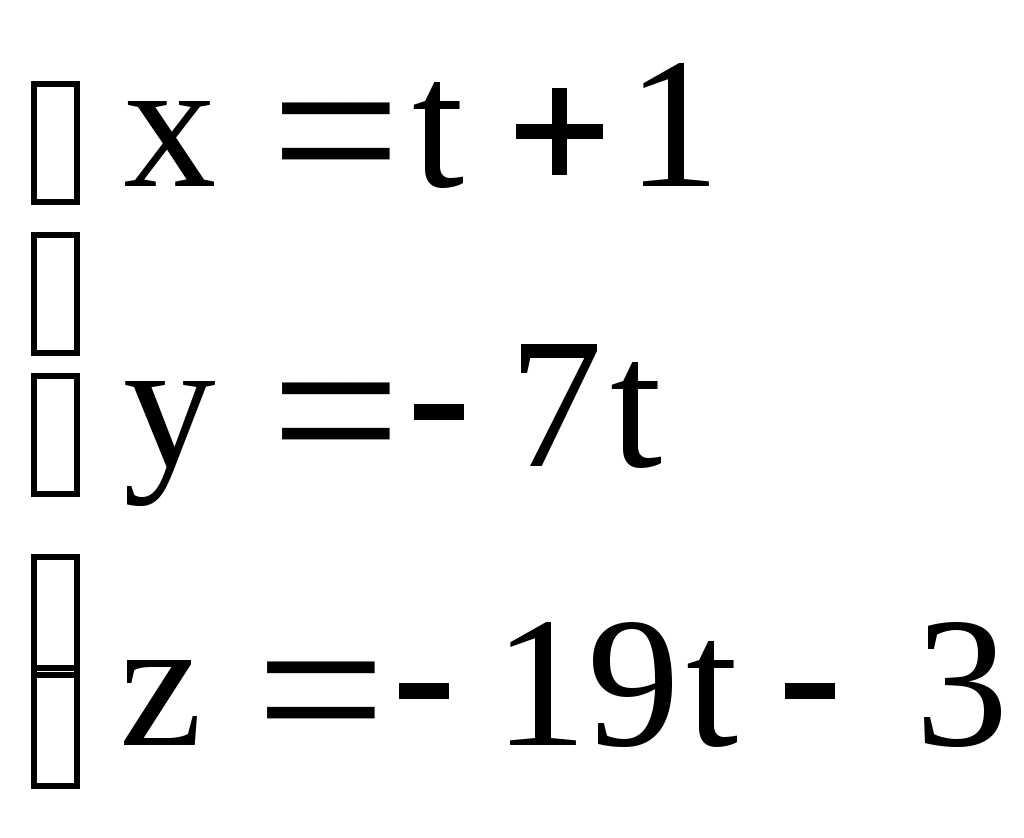 . 4. . 4. б) Пересекаются, (2;-3;6), 6. а) 9. 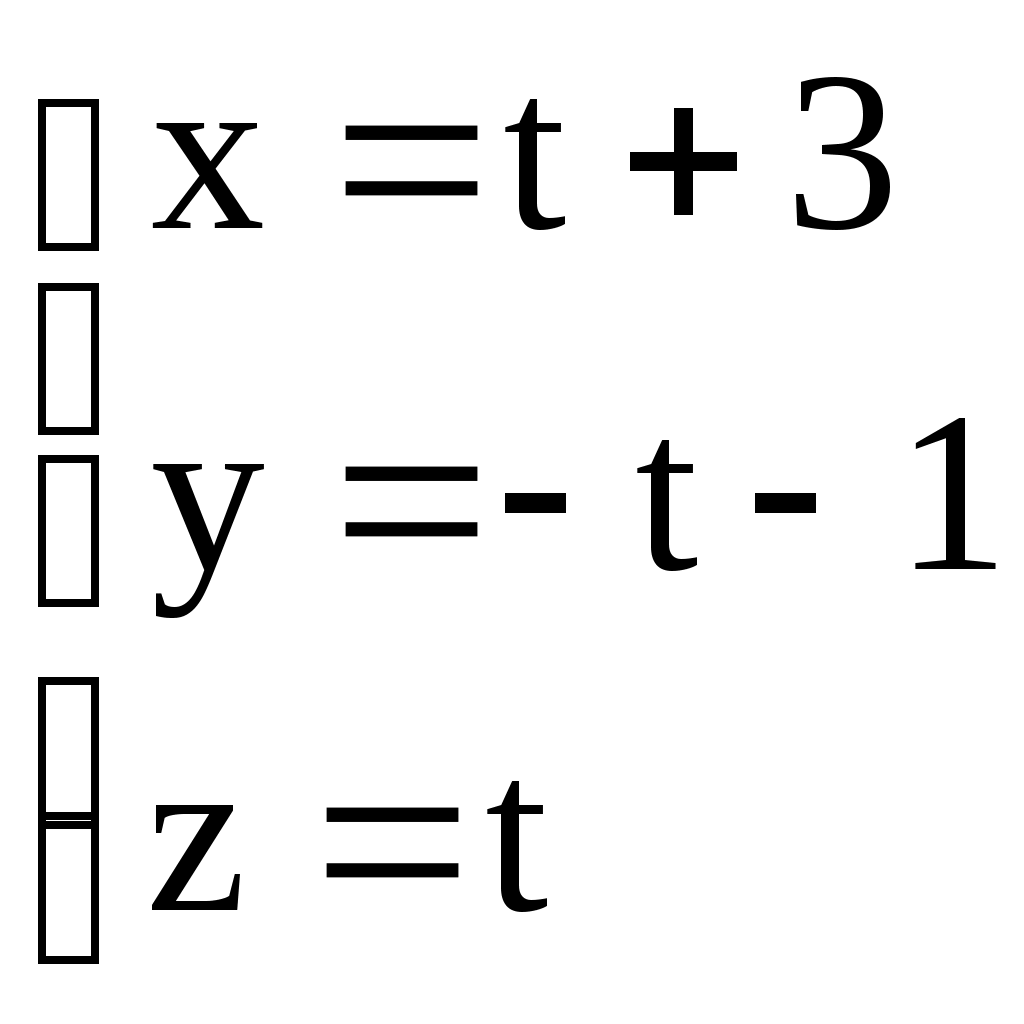 . 10. . 10. 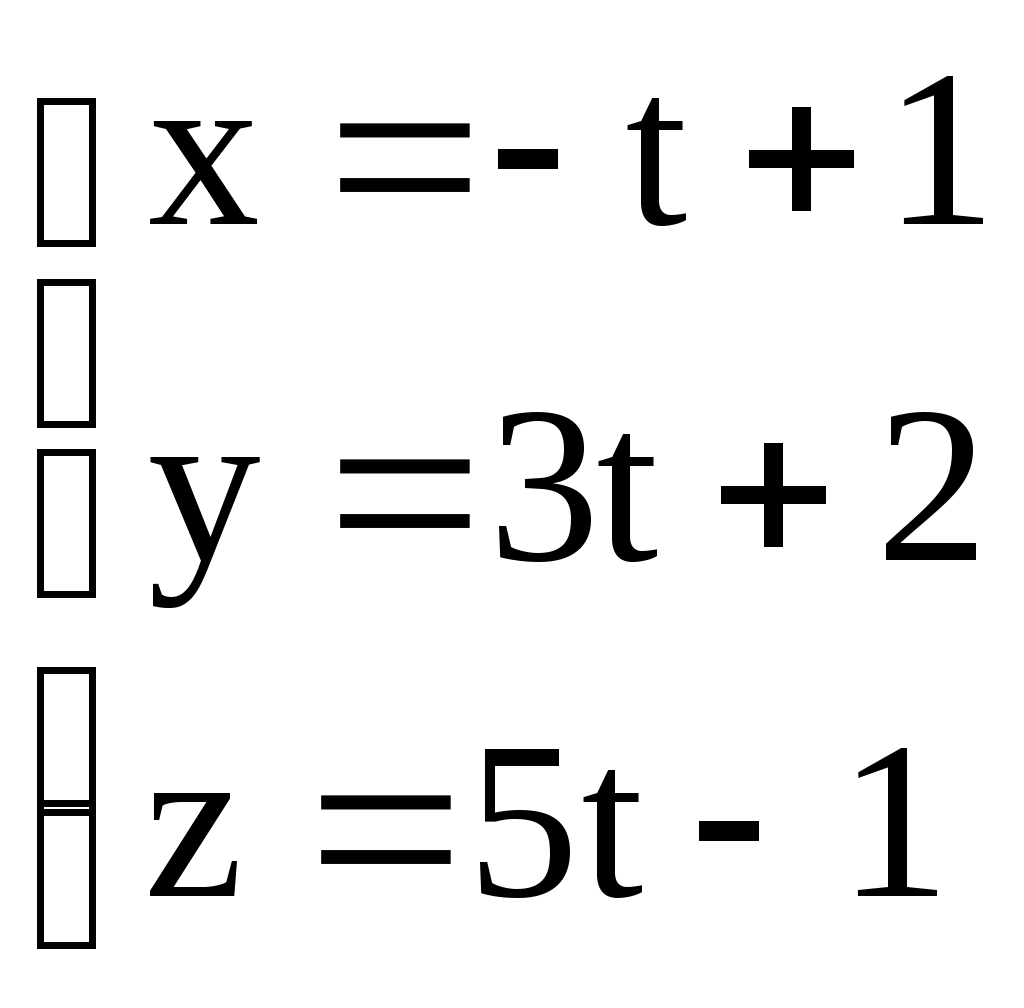 . 11. . 11. 12. 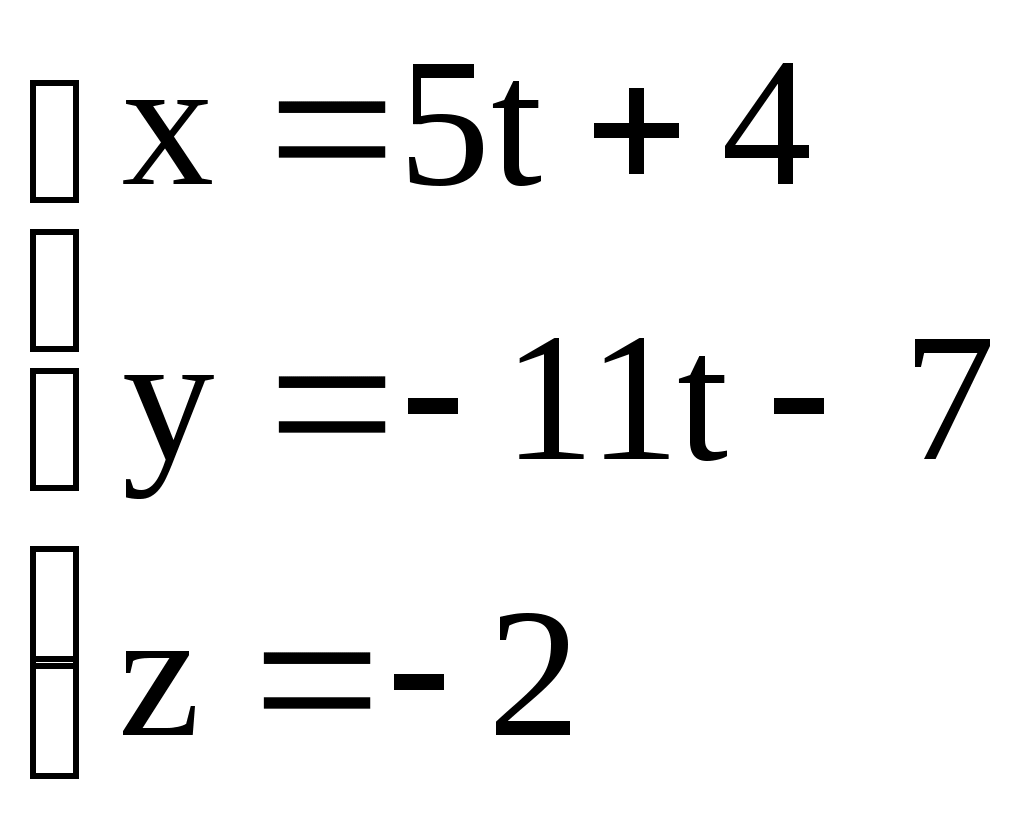 . 13. а) Пересекаются, (-1;-2;1), . 13. а) Пересекаются, (-1;-2;1), |