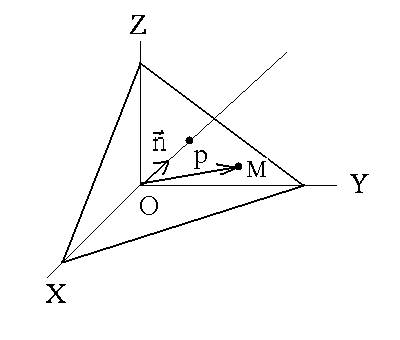Глава. Глава 3. Аналитическая геометрия

• Название: Аналитическая геометрия
• Анкор: Глава
• Дата: 16.10.2021
• Размер: 1.38 Mb.
• Имя файла: Глава 3.doc
• Тип: Глава; #248873
• страница: 3 из 6

3.3.1. Виды уравнений плоскости
Рассмотрим какие-нибудь три произвольные точки 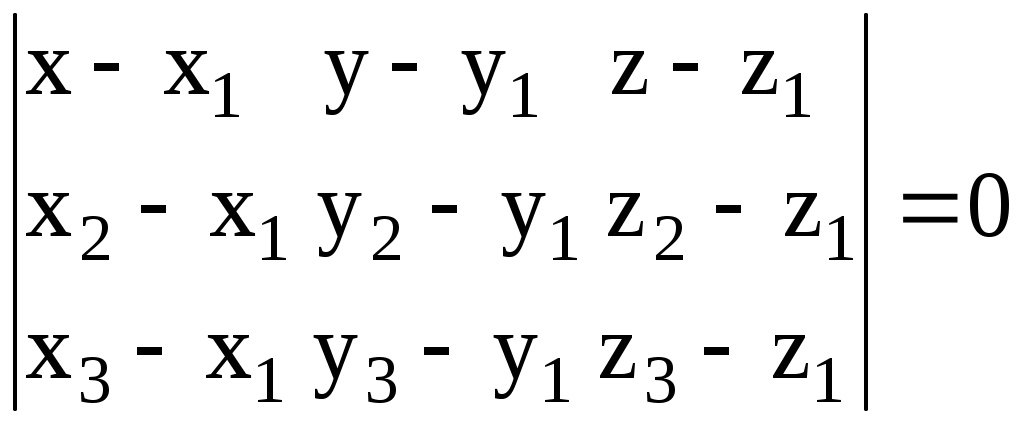, и , не лежащие на одной прямой. Построим на этих точках два вектора и , которые являются неколлинеарными и их можно использовать в качестве направляющих векторов плоскости. Тогда уравнение плоскости, проходящей через точку с указанными направляющими векторами, запишется в виде
. (3.25)
Это и есть уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.

Рассмотрим теперь произвольный единичный вектор

, лежащий на луче, проведенном из начала координат. Выберем на нем произвольную точку P и обозначим через OP = p расстояние от начала координат до этой точки. Далее, проведем через точку Р плоскость, перпендикулярную вектору . Такая плоскость единственная и ее

уравнение есть , где - произвольная точка этой плоскости. Это уравнение можно записать в виде или
. (3.26)
Это и есть уравнение плоскости в нормальном виде или нормированное уравнение плоскости. Если - произвольная точка, не лежащая на плоскости (3.25), то величина

называется отклонением точки от плоскости, определяемой уравнением (3.26). Если , то это означает, что точка и начало координат лежат по разные стороны от плоскости, и если - то по одну. Если же начало координат O лежит на плоскости, то положим , если лежит по ту сторону от плоскости, куда направлен вектор и в противном случае. Расстояние от этой точки до плоскости . Чтобы привести общее уравнение плоскости к нормальному виду, достаточно умножить его, по аналогии с общим уравнением прямой на плоскости, на нормирующий множитель , знак которого выбирается противоположным знаку D. Тогда отклонение точки от плоскости определится как
(3.27)
и расстояние от точки до плоскости .

3.3.2. Угол между двумя плоскостями
Пусть две плоскости заданы своими общими уравнениями и . Тогда угол между ними будет равен углу между их нормальными векторами и , который определится из скалярного произведения этих векторов

. (3.28)
Отсюда следуют условие перпендикулярности двух плоскостей (ортогональность нормальных векторов) и параллельности двух плоскостей (коллинеарность нормальных векторов) .
3.4. ЗАДАЧИ
1. Составить уравнение плоскости в отрезках, если эта плоскость проходит через точку и имеет нормальный вектор .

2. Составить уравнение плоскости, проходящей через точки , , .

3. Составить уравнение плоскости, проходящей через точку и

а) параллельно координатной плоскости ;

б) проходящей через ось .

4. Составить уравнение плоскости, проходящей через точку и

а) параллельно двум векторам , ;

б) перпендикулярно вектору , где ;

в) перпендикулярно вектору , где О - начало координат;

г) проходящей через точку и параллельно вектору .

4. Определить взаимное расположение плоскостей (пересекаются, параллельны, совпадают). Если плоскости пересекаются, то найти угол между ними; если плоскости параллельны, то найти расстояние между ними:

а) , ;

б) , ;

в) , .

5. На оси найти точку, равноудаленную от плоскостей

и .

6. Найти объем пирамиды, ограниченной плоскостями

, , , .
Домашнее задание.
7. Составить уравнение плоскости, проходящей через точки

, , .

8. Составить уравнение плоскости, проходящей через точку и

а) параллельно координатной плоскости ;

б) проходящей через прямую в плоскости .

9. Составить уравнение плоскости в общем виде и в отрезках, если плоскость проходит через точку и

а) параллельно двум векторам , ;

б) перпендикулярно вектору , где ;

в) проходящей через точку и параллельно вектору .

10. Определить взаимное расположение плоскостей (пересекаются, параллельны, совпадают). Если плоскости пересекаются, то найти угол между ними; если плоскости параллельны, то найти расстояние между ними:

а) , ;

б) , ;

в) , .

11. Найти плоскость, равноудаленную от плоскостей

и .

Ответы. 1. . 2. . 3. а) ;

б) . 4. а) ; б) ;

в) ; г) .

5. а) Пересекаются, ; б) Совпадают; в) Параллельны, .

6. , . 7. . 8. .

9. а) ; б) . 9. а) ; б) ;

в) . 10. а) Параллельны, ; б) Совпадают;

в) Пересекаются, . 11. .

3.5. Прямая линия в пространстве
Выберем в пространстве произвольную фиксированную точку и фиксированный ненулевой вектор , который будем называть направляющим вектором прямой. Точка тогда и только тогда лежит на прямой, проходящей через точку параллельно направляющему вектору , когда векторное произведение векторов и равно нулю:
или . (3.29)
Уравнение (3.29) называется уравнением прямой в векторном виде. В декартовых координатах это уравнение записывается в виде условия коллинеарности указанных векторов
(3.30)
и называется каноническим уравнением прямой. Любая координата вектора 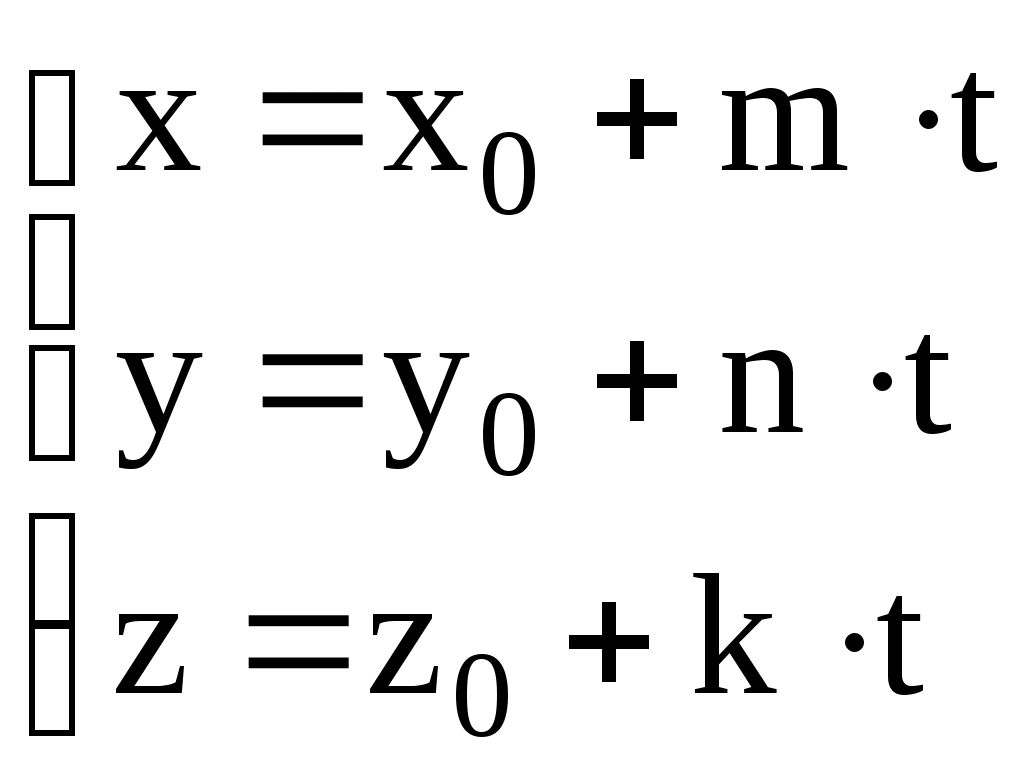(но не все одновременно) может быть равна нулю. Это означает, что прямая будет проходить параллельно соответствующей координатной плоскости. Уравнение (3.30) также может быть представлено в параметрическом виде (параметрическое уравнение прямой)

, (3.31)
где t - произвольный параметр. Кроме того, как известно, пересечение двух непараллельных плоскостей происходит по прямой и поэтому можно уравнение прямой задать в виде системы двух уравнений первого порядка, каждое из которых является общим уравнением плоскости: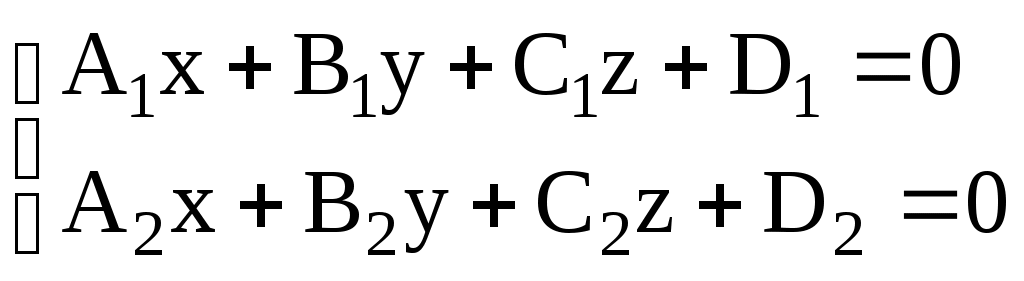
. (3.32)
Покажем, что система (3.32) действительно является уравнением прямой. Поскольку плоскости непараллельные, ранг матрицы системы уравнений (3.32) равен двум. Пусть, например, базисным минором этой системы есть . Тогда общее решение системы (3.32) имеет вид: , где - числа. Его можно записать в виде , это и есть каноническое уравнение прямой.

Получим уравнение прямой, проходящей через две заданные точки. Пусть это будут точки и . В качестве направляющего вектора прямой возьмем вектор и тогда уравнение прямой, проходящей через две заданные точки, имеет вид:
(3.33)