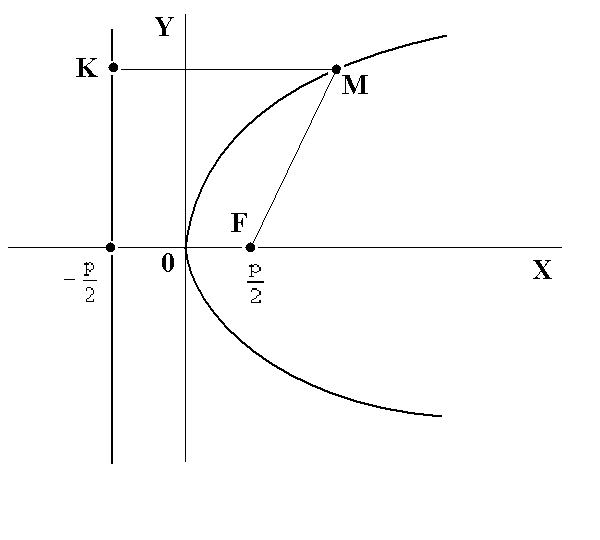|
|
Глава. Глава 3. Аналитическая геометрия
3.7. Кривые второго порядка на плоскости.
Введем на плоскости прямоугольную декартову систему координат и рассмотрим кривую, определяемую неявно общим алгебраическим уравнением второй степени
 , (3.35) , (3.35)
где: A, B, C, D, E, F – некоторые числа, причем A, B, C не равны нулю одновременно. Кривая в декартовых координатах, описываемая уравнением (3.35), называется кривой второго порядка. Может случиться так, что уравнению (3.35) не соответствует ни одна точка с вещественными координатами (x, y) и тогда уравнение (3.35) определяет мнимую кривую второго порядка. Например, уравнению 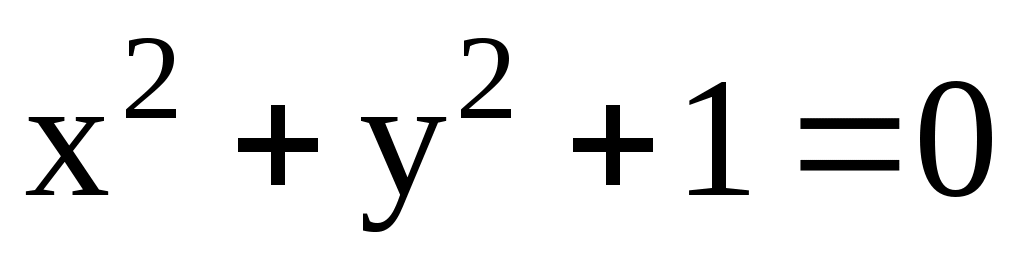 не соответствует ни одна точка в декартовой системе координат. В дальнейшем такие кривые не рассматриваются. не соответствует ни одна точка в декартовой системе координат. В дальнейшем такие кривые не рассматриваются.
Перечислим шесть важных случаев общего уравнения кривых второго порядка (канонические кривые).
1). Уравнение эллипса:  с полуосями a, b. При a = b - окружность с центром в начале координат. с полуосями a, b. При a = b - окружность с центром в начале координат.
2). Уравнение гиперболы:  с полуосями a, b. с полуосями a, b.
3). Уравнение параболы:  . .
4). Уравнение пары пересекающихся прямых: 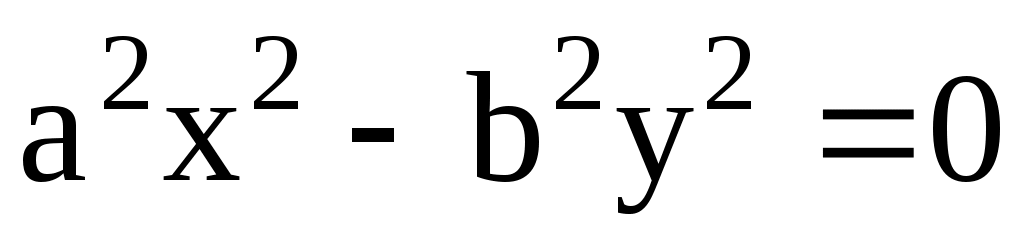 . .
5). Уравнение пары параллельных прямых: 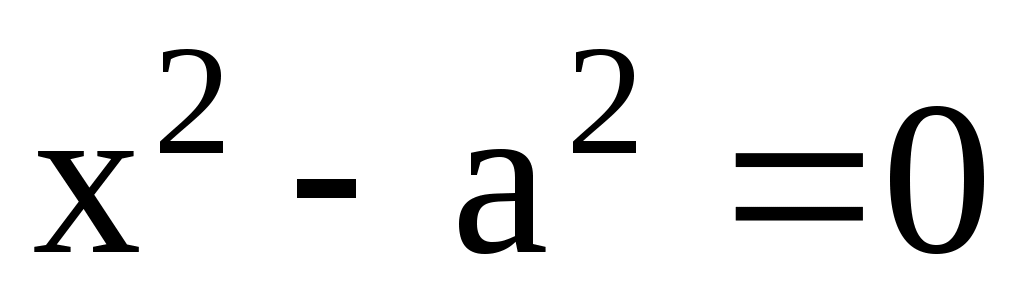 или или 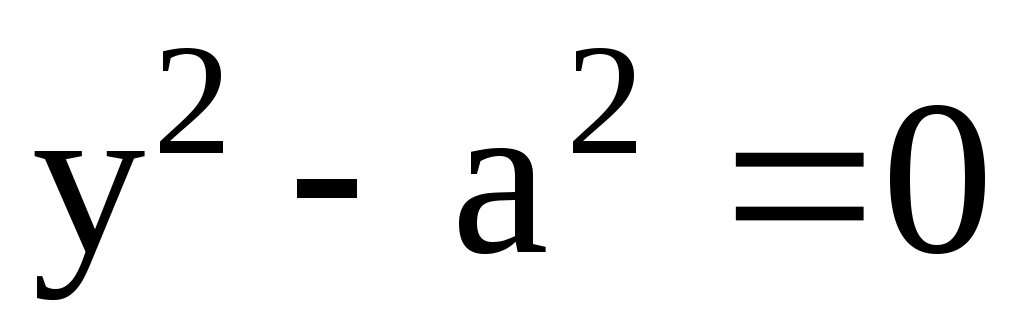 . .
6). Уравнение, определяющее точку:  . .
Рассмотрим вкратце эти канонические кривые и некоторые их свойства.
3.7.1. Эллипс.
Уравнение эллипса
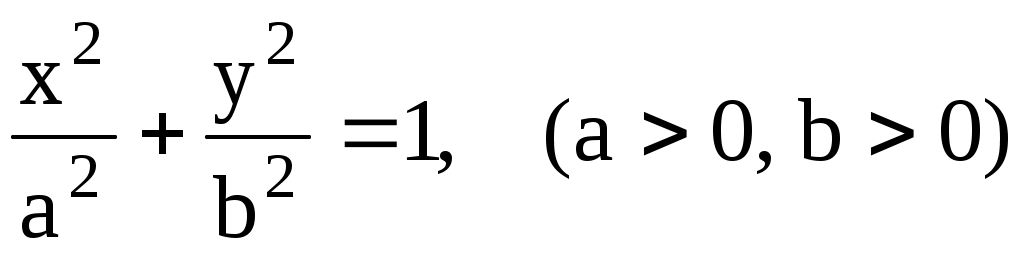 (3.36) (3.36)
с полуосями a, b. Нетрудно видеть, что это кривая, симметричная относительно начала координат. Такие кривые называются центральными кривыми. Точки 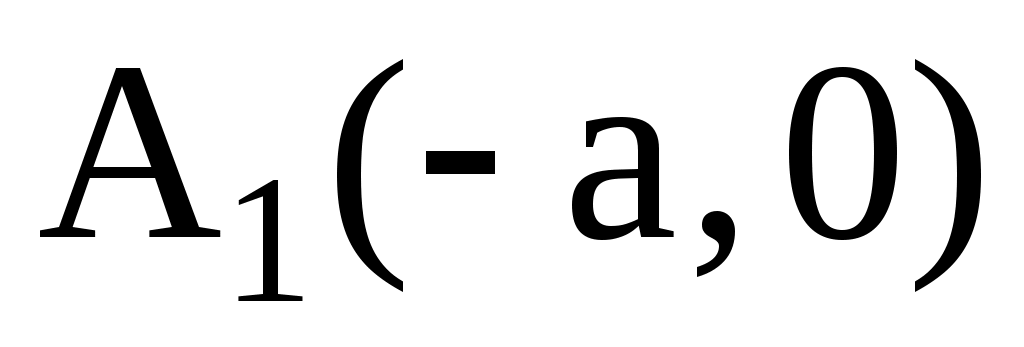 , ,  , , 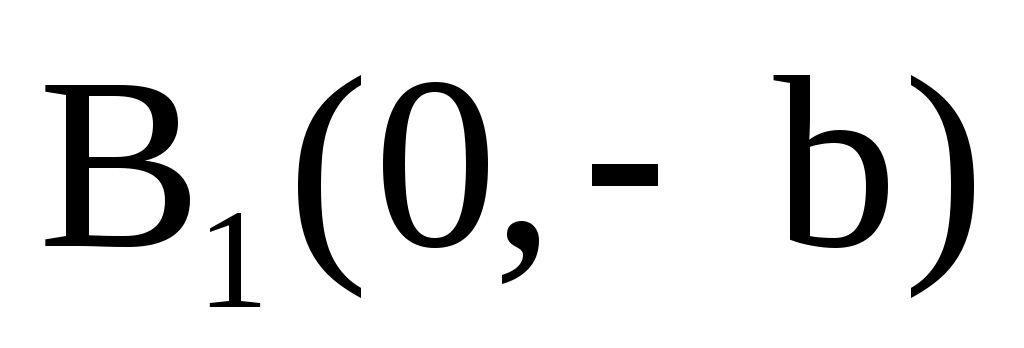 , , 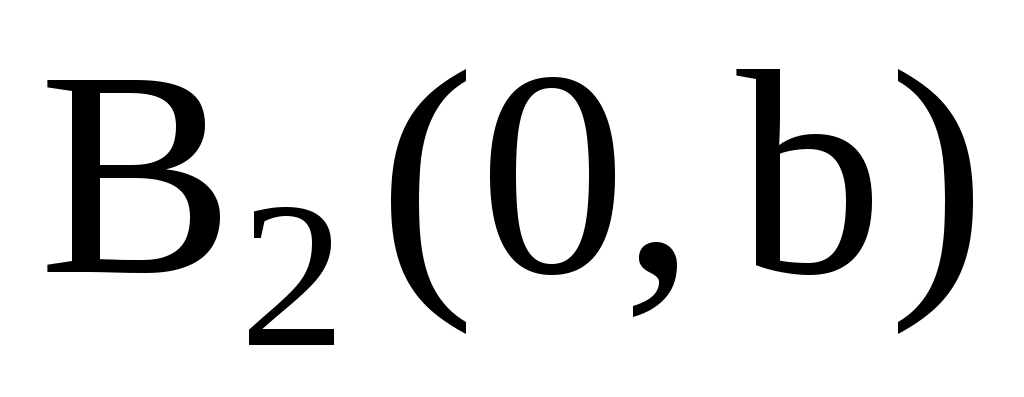 называются вершинами эллипса. Пусть для определенности называются вершинами эллипса. Пусть для определенности
a > b. Положим 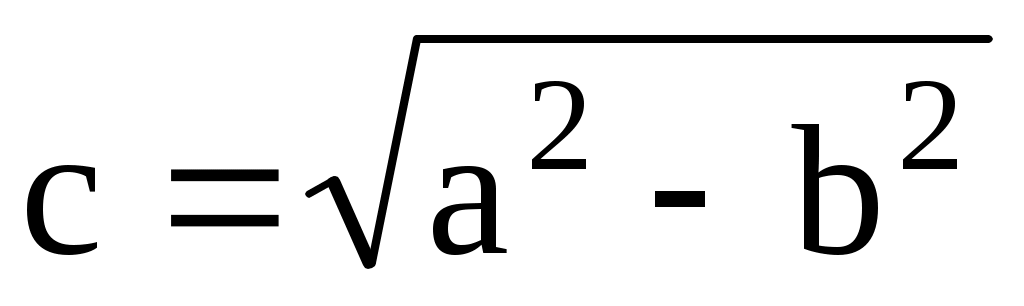 и отметим на оси X точки и отметим на оси X точки  и и  , отстоящие от начала координат на расстоянии , отстоящие от начала координат на расстоянии 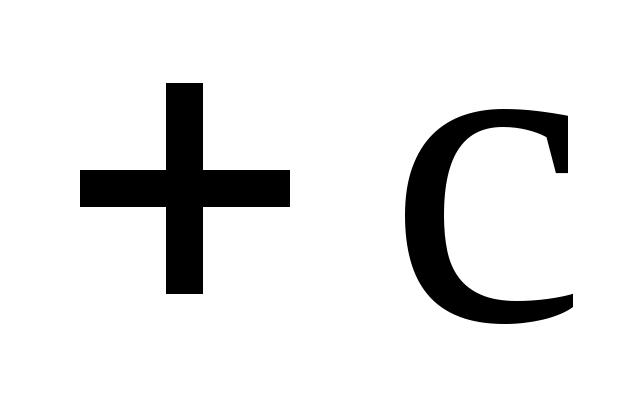 и и 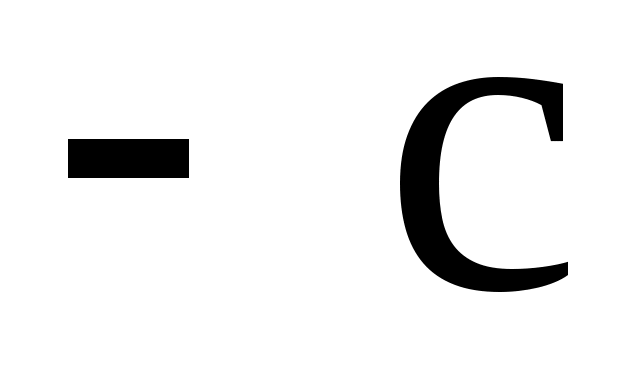 соответственно. Эти точки называются фокусами эллипса. Эллипс определяется как геометрическое место точек, сумма расстояний которых до фокусов соответственно. Эти точки называются фокусами эллипса. Эллипс определяется как геометрическое место точек, сумма расстояний которых до фокусов  и и  есть величина постоянная, равная 2а. есть величина постоянная, равная 2а.
Действительно,  
 , откуда , откуда 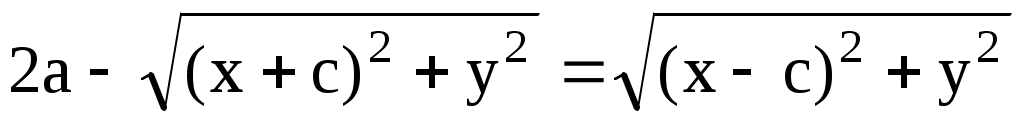
и 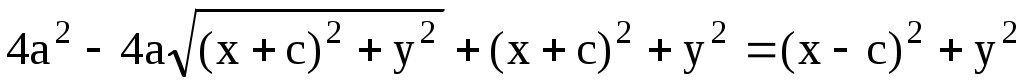
или 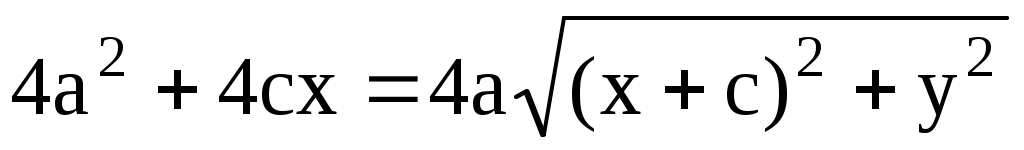 . Возводя в квадрат обе части, получим . Возводя в квадрат обе части, получим 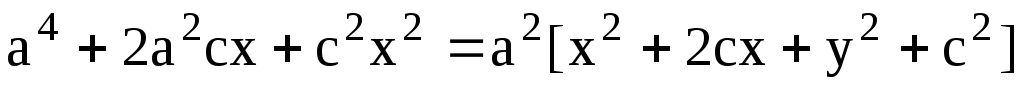 . .
Так как 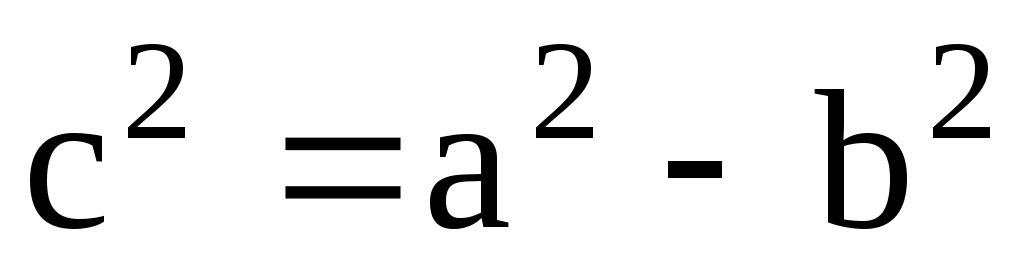 , то , то 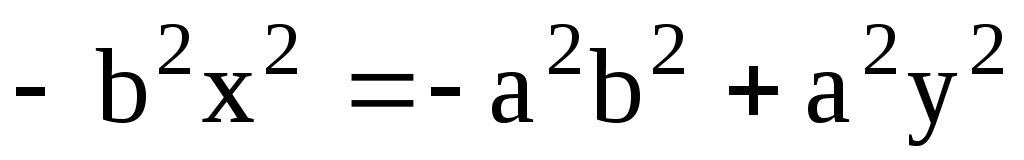 и, поделив обе части на и, поделив обе части на 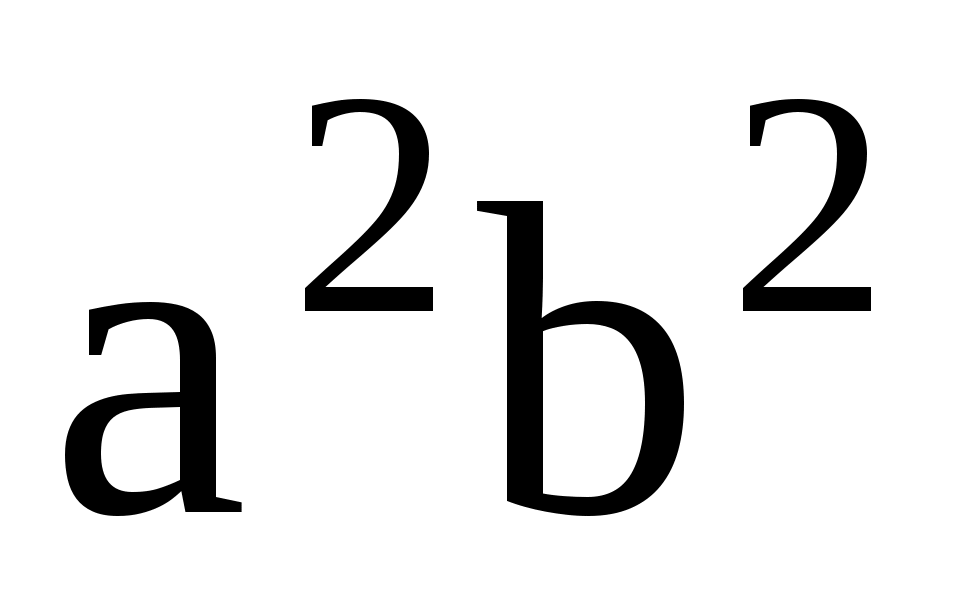 , получим уравнение эллипса , получим уравнение эллипса 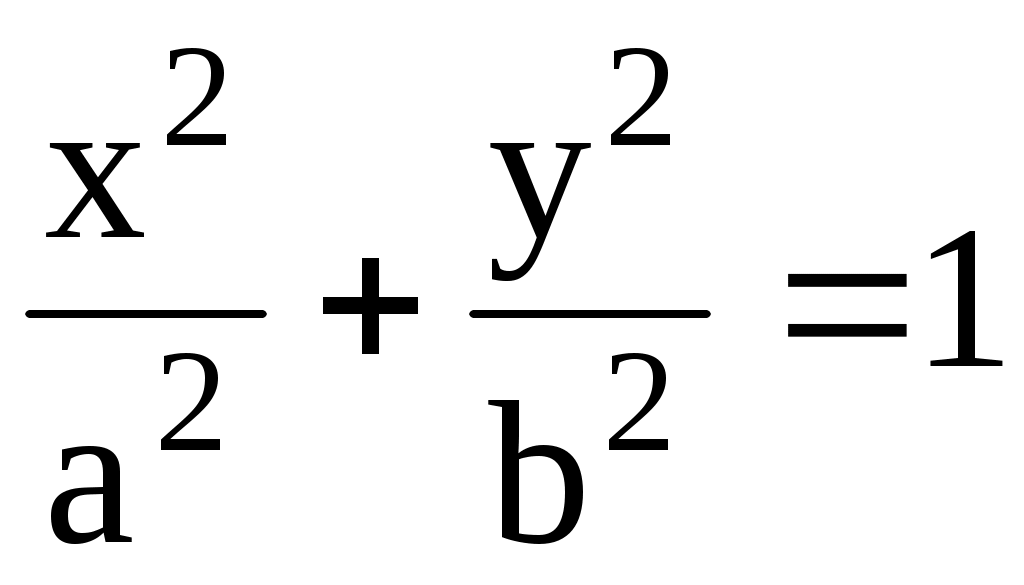 . Величина . Величина  называется эксцентриситетом эллипса ( называется эксцентриситетом эллипса (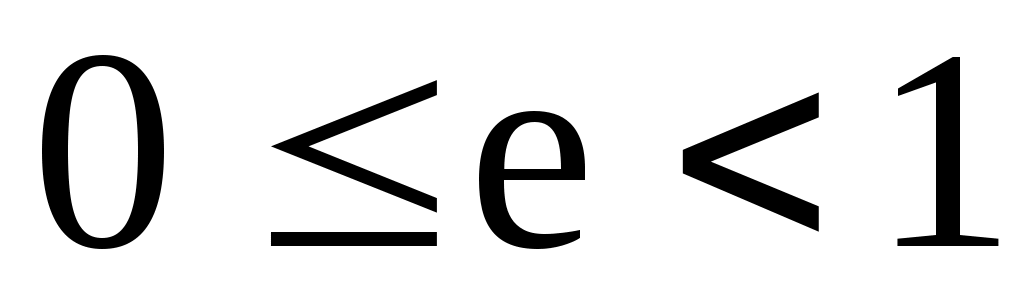 ) и характеризует «сплюснутость» эллипса вдоль полуоси a. При c = 0 (a = b) имеем уравнение окружности, при ) и характеризует «сплюснутость» эллипса вдоль полуоси a. При c = 0 (a = b) имеем уравнение окружности, при  ( ( ) эллипс переходит в отрезок прямой [-a, a]. Уравнение эллипса также можно записать в параметрическом виде ) эллипс переходит в отрезок прямой [-a, a]. Уравнение эллипса также можно записать в параметрическом виде
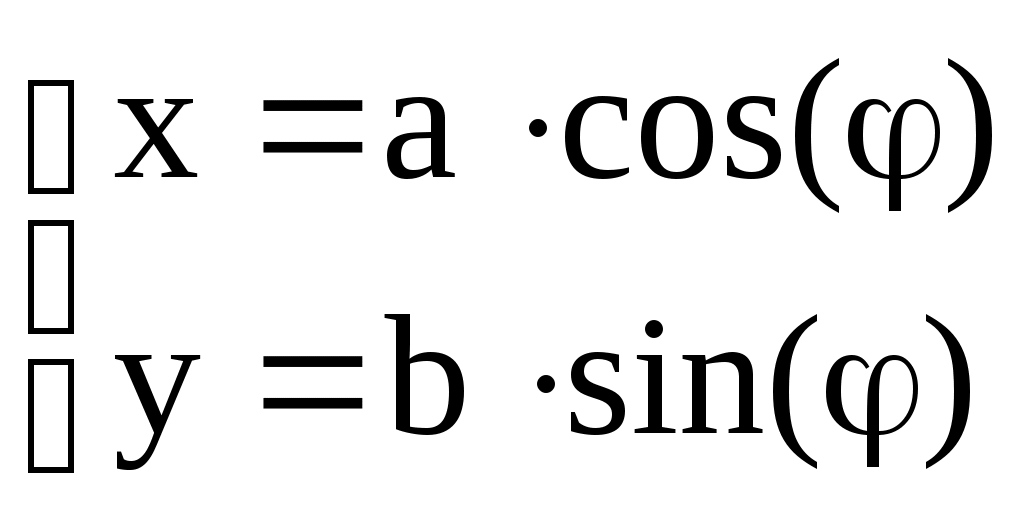 , , 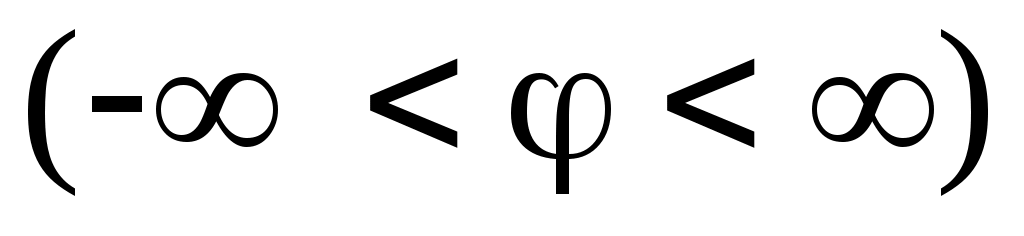 . (3.37) . (3.37)
Действительно, 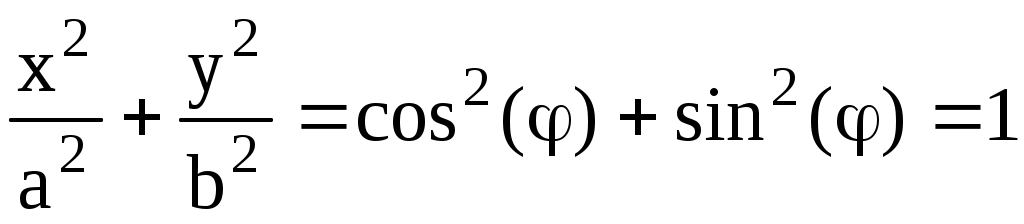 . .
Если начало координат перенести в точку  , то в новых декартовых же координатах , то в новых декартовых же координатах 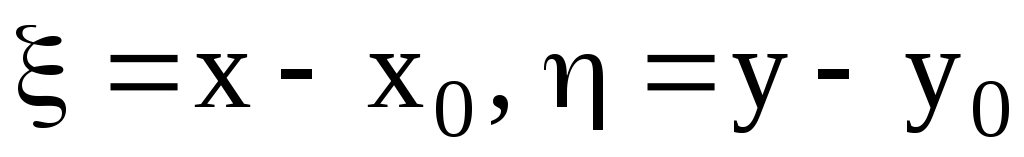 уравнение эллипса по-прежнему будет иметь канонический вид уравнение эллипса по-прежнему будет иметь канонический вид  , а в старых (исходных) запишется как , а в старых (исходных) запишется как
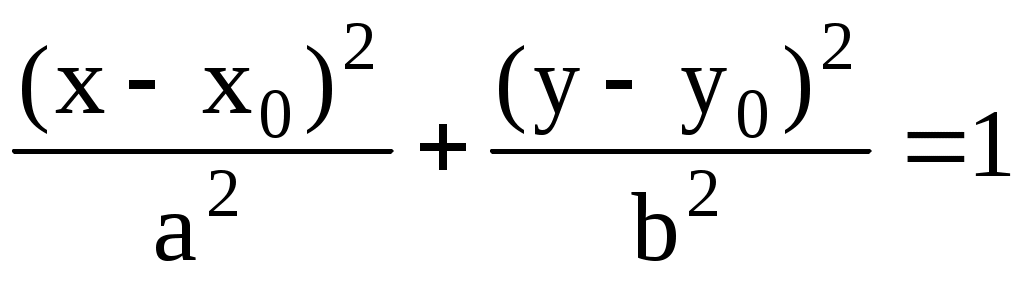 (3.38) (3.38)
3.7.2. Гипербола.
Уравнение гиперболы
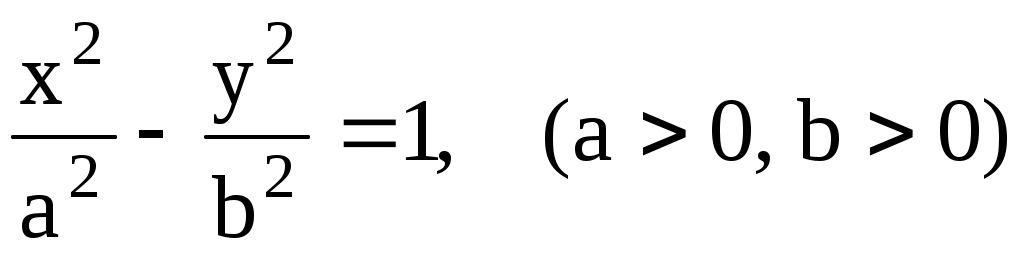 . (3.39) . (3.39)
Это также центральная кривая. Параметры a и b называются полуосями гиперболы. Точки ее пересечения с осью ОХ с абсциссами x = a и 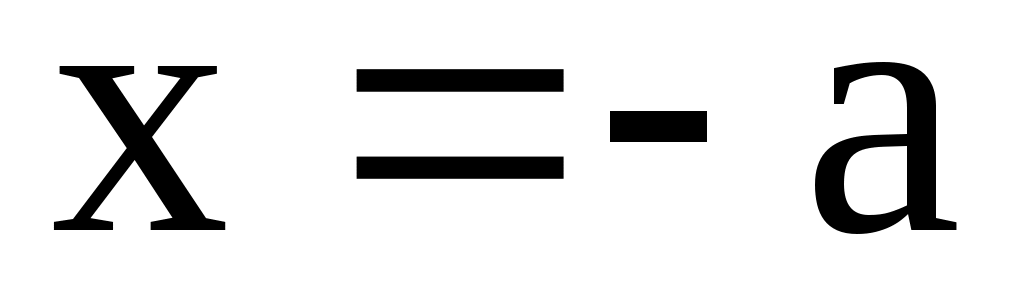 называются вершинами гиперболы, ось OX – ее действительной осью. Ось OY гипербола не пересекает, и эта ось называется мнимой осью гиперболы, а точки называются вершинами гиперболы, ось OX – ее действительной осью. Ось OY гипербола не пересекает, и эта ось называется мнимой осью гиперболы, а точки 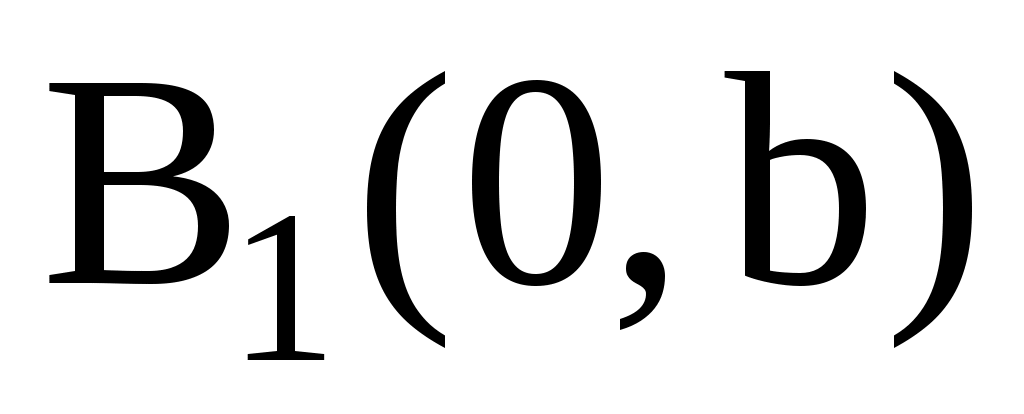 и и  называются ее мнимыми вершинами. Положим называются ее мнимыми вершинами. Положим  и отметим на оси X точки и отметим на оси X точки  и и  с абсциссами с абсциссами  и и 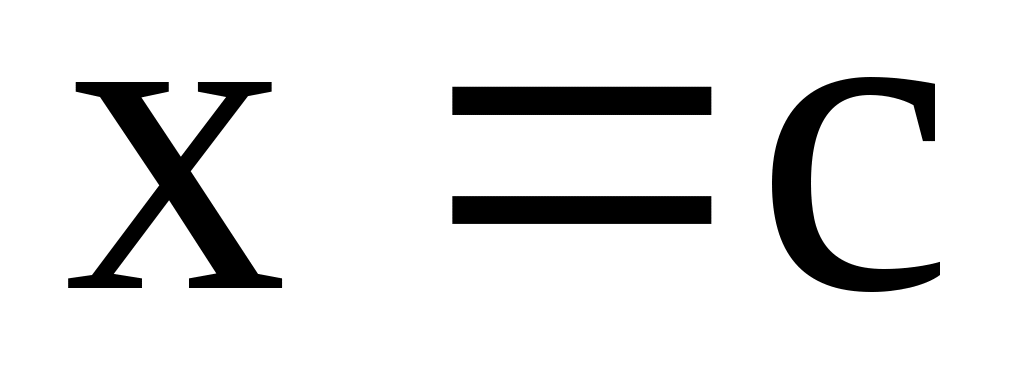 соответственно, которые называются ее фокусами. Расстояние между фокусами соответственно, которые называются ее фокусами. Расстояние между фокусами 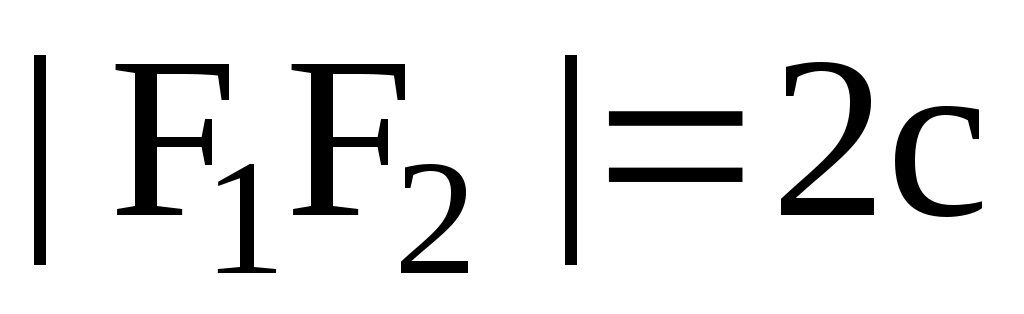 называется фокальным расстоянием. Гипербола определяется как геометрическое место точек, разность расстояний которых до фокусов называется фокальным расстоянием. Гипербола определяется как геометрическое место точек, разность расстояний которых до фокусов  и и  есть величина постоянная, равная 2a. есть величина постоянная, равная 2a.
По определению, имеем, выбирая в качестве расстояния разность 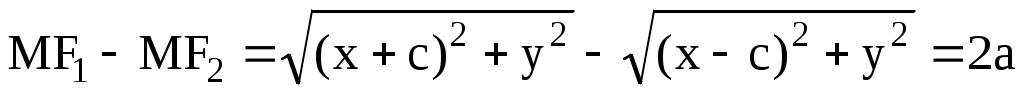 , получим первую (правую) ветвь гиперболы. Далее: , получим первую (правую) ветвь гиперболы. Далее: 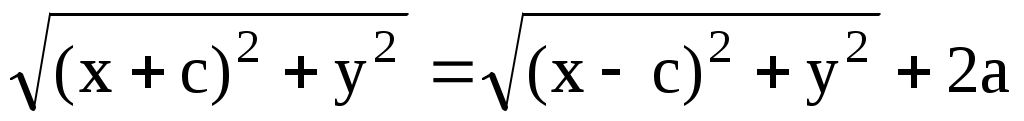 . Возведем в квадрат обе части . Возведем в квадрат обе части 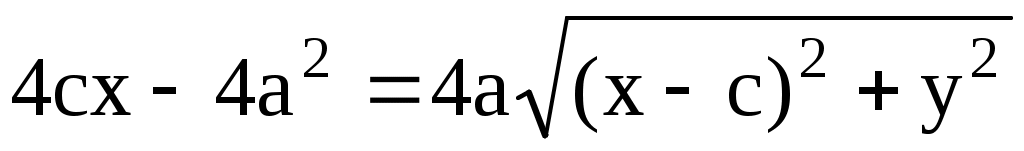 или, снова возводя в квадрат, получим или, снова возводя в квадрат, получим  . Отсюда . Отсюда 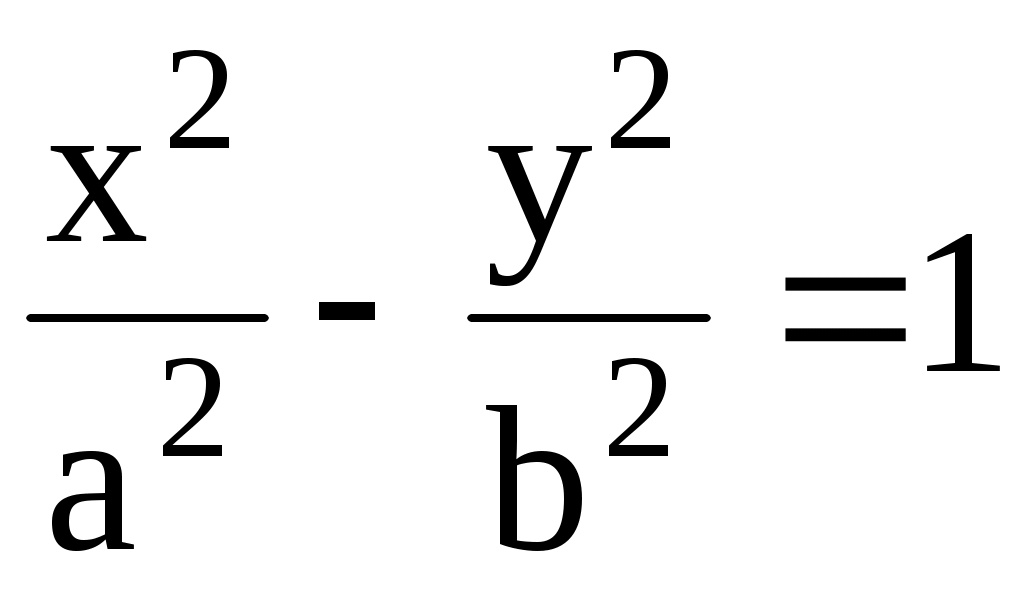 . Если исходить из равенства . Если исходить из равенства  , то аналогичным образом получим вторую (левую) ветвь гиперболы. Уравнение гиперболы можно также записать в виде , то аналогичным образом получим вторую (левую) ветвь гиперболы. Уравнение гиперболы можно также записать в виде 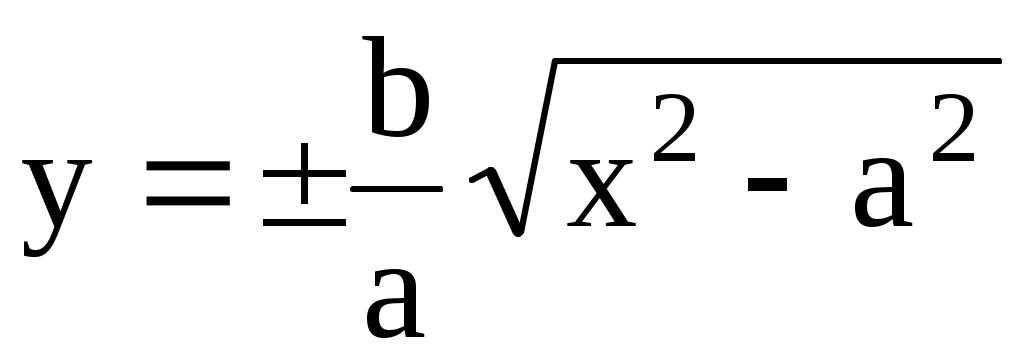 . Тогда . Тогда 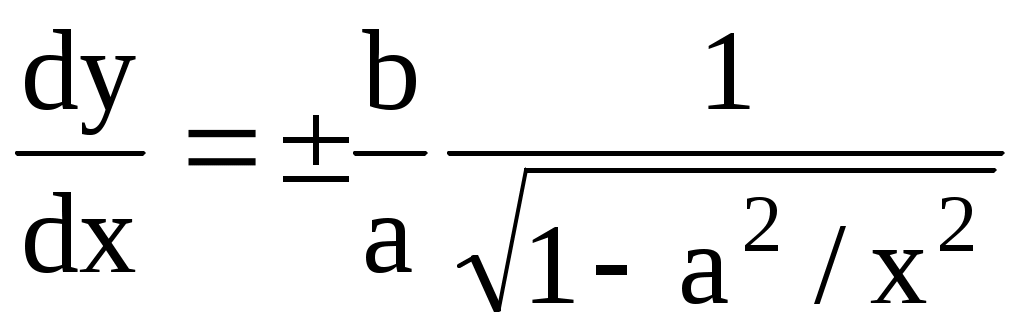 и при и при  получаем уравнения двух прямых получаем уравнения двух прямых 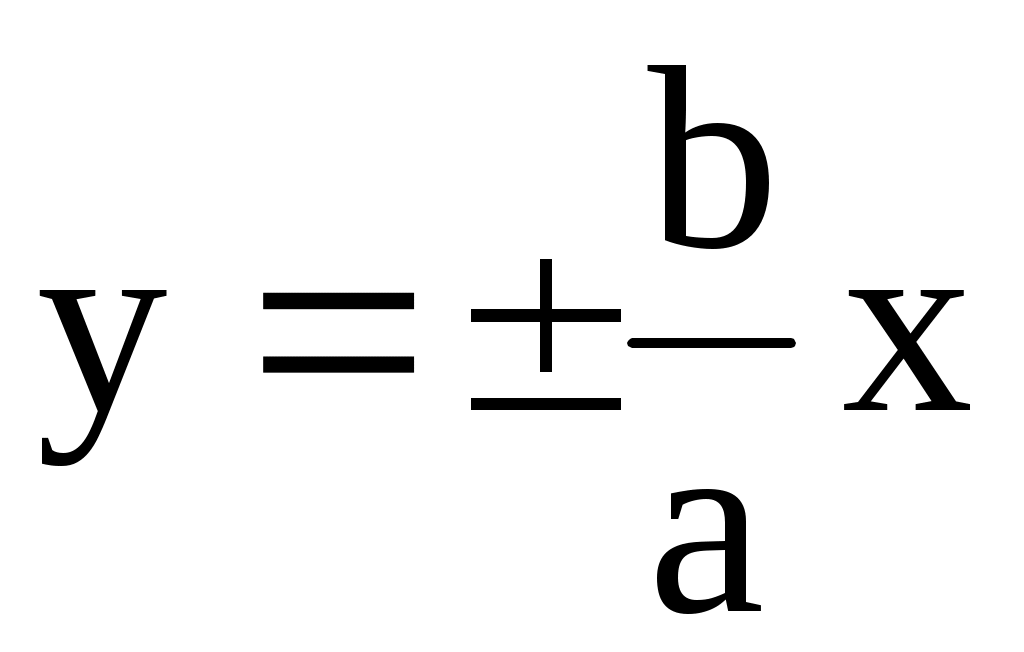 , которые являются асимптотами гиперболы. Эксцентриситет гиперболы , которые являются асимптотами гиперболы. Эксцентриситет гиперболы 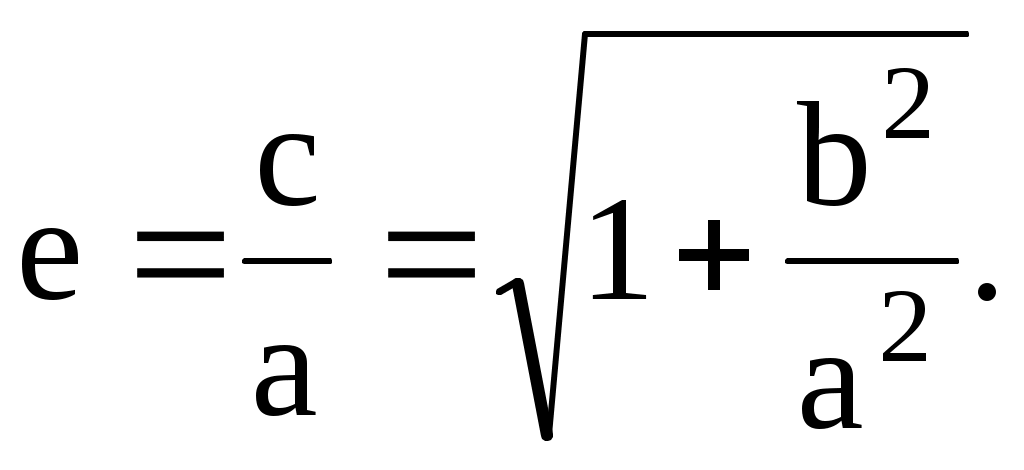 Нетрудно видеть, что Нетрудно видеть, что 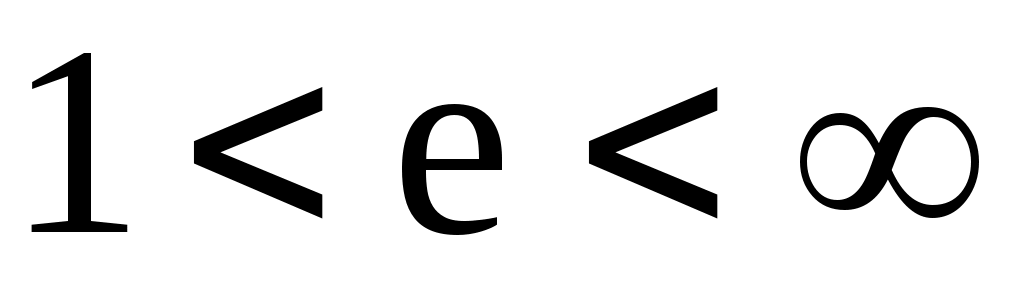 и также характеризует ее «сплюснутость». При и также характеризует ее «сплюснутость». При  гипербола приближается к своему вырожденному состоянию – двум полупрямым на действительной оси. гипербола приближается к своему вырожденному состоянию – двум полупрямым на действительной оси.
По аналогии с параметрическим уравнением эллипса, можно записать параметрическое уравнение гиперболы
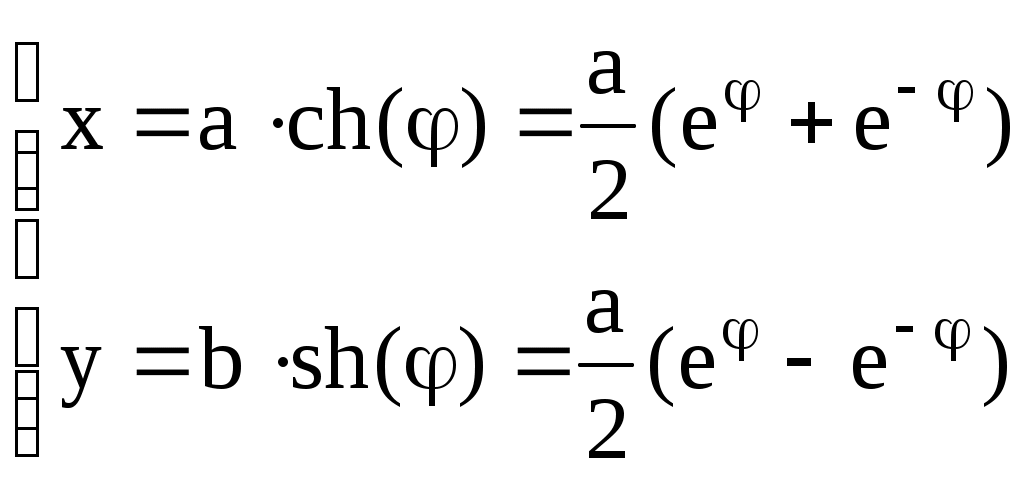 , (3.40) , (3.40)
Действительно, 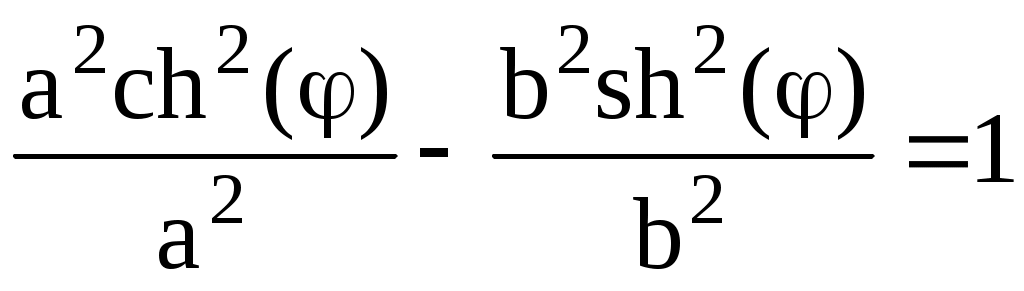 . Если начало координат перенести в точку . Если начало координат перенести в точку  , то в новых декартовых же координатах , то в новых декартовых же координатах 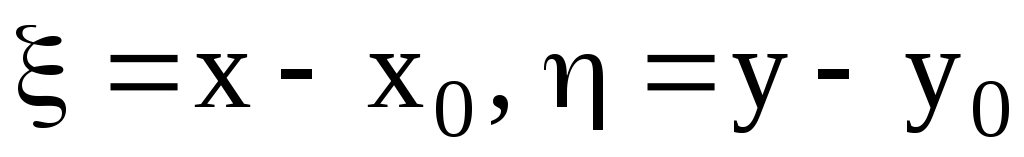 уравнение гиперболы по-прежнему будет иметь канонический вид уравнение гиперболы по-прежнему будет иметь канонический вид 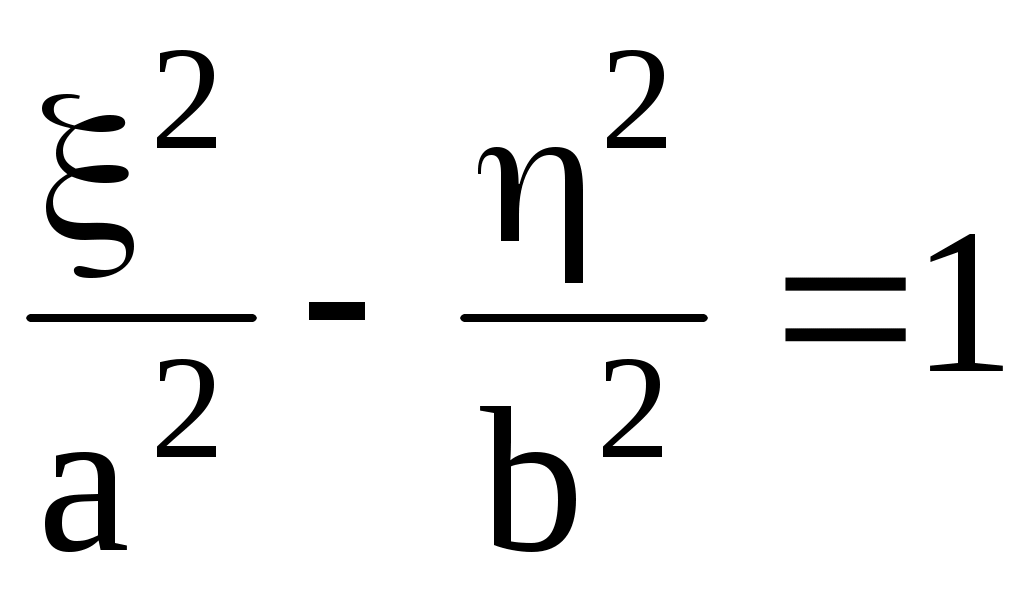 , а в старых (исходных) запишется как , а в старых (исходных) запишется как
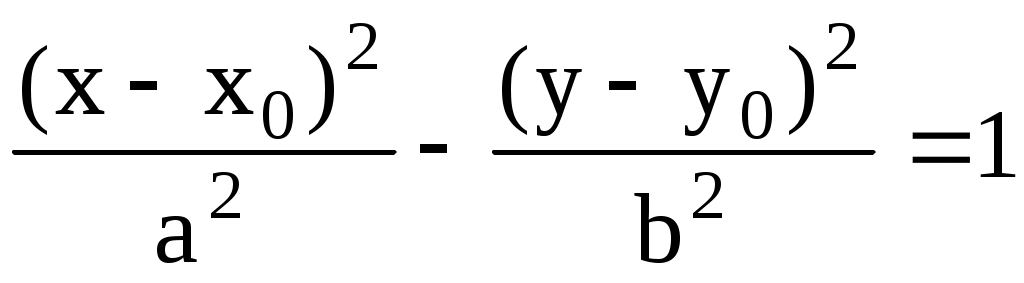 . (3.41) . (3.41)
3.7.3. Парабола
Каноническое уравнение параболы имеет вид
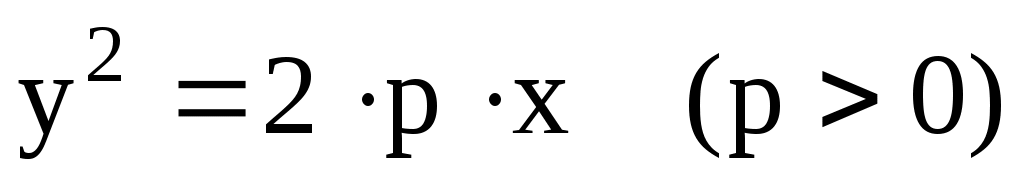 , (3.42) , (3.42)
которая является нецентральной линией. Точка F на оси абсцисс 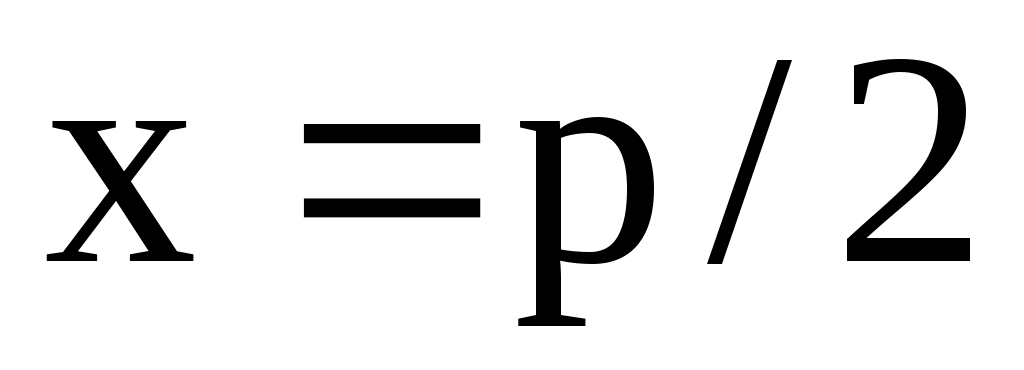 называется фокусом параболы, а прямая называется фокусом параболы, а прямая 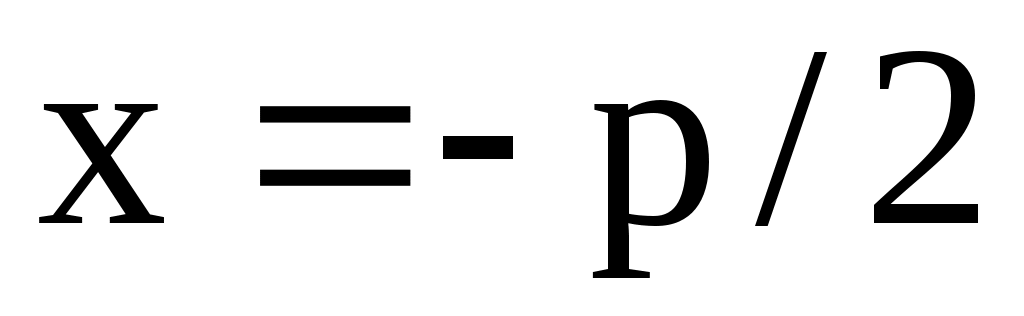 называется директрисой параболы. Тогда парабола определяется как геометрическое место точек M(x, y), равноудаленных от фокуса и директрисы. называется директрисой параболы. Тогда парабола определяется как геометрическое место точек M(x, y), равноудаленных от фокуса и директрисы.
Действительно,
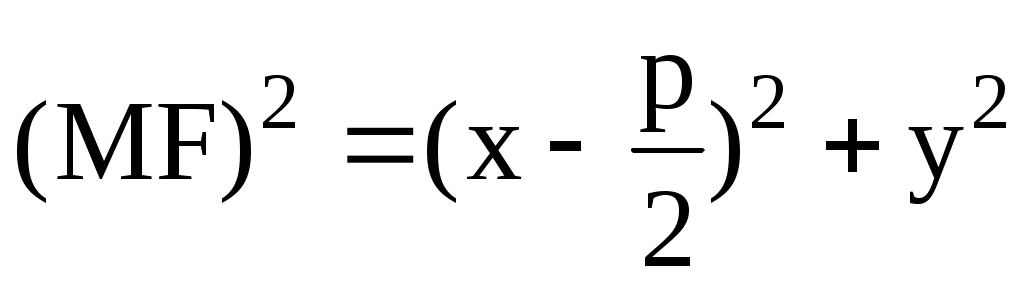 , , , , 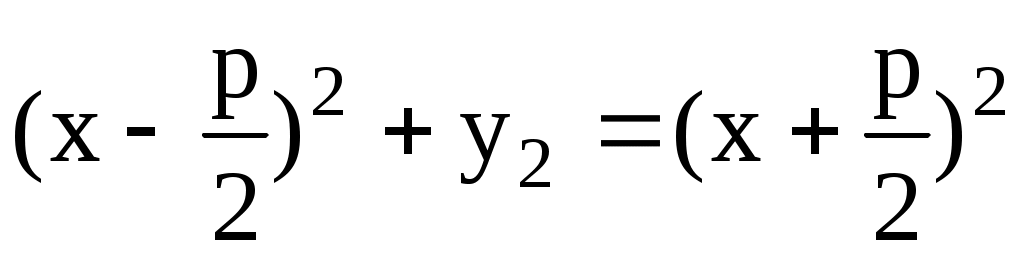 , то есть, , то есть, 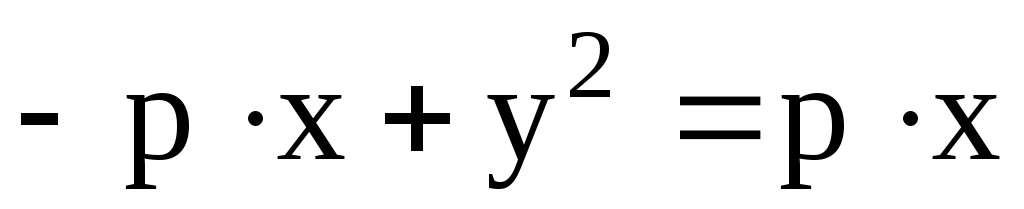 или или  . Парабола не имеет асимптот. Если начало координат перенести в точку . Парабола не имеет асимптот. Если начало координат перенести в точку  , то в новых декартовых же координатах , то в новых декартовых же координатах 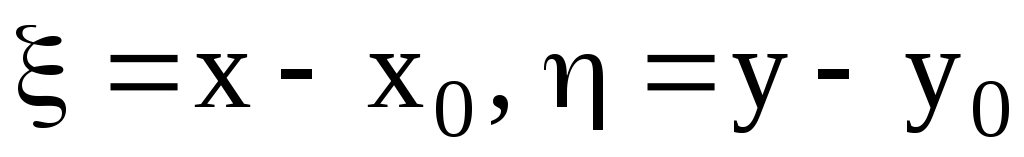 уравнение параболы также по-прежнему будет иметь канонический вид уравнение параболы также по-прежнему будет иметь канонический вид 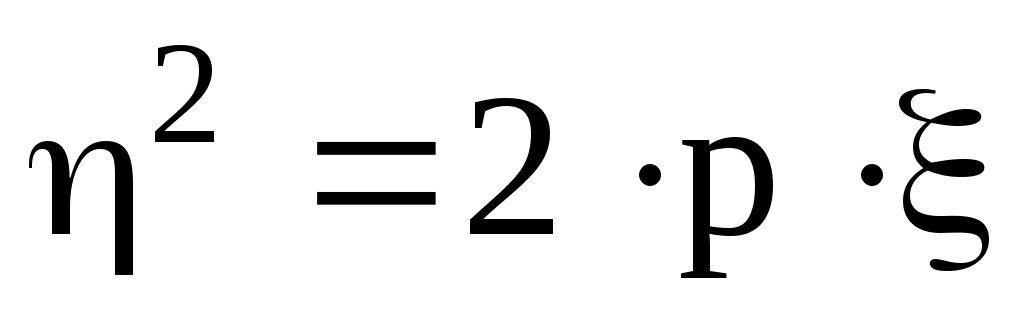 , а в старых (исходных) запишется как , а в старых (исходных) запишется как
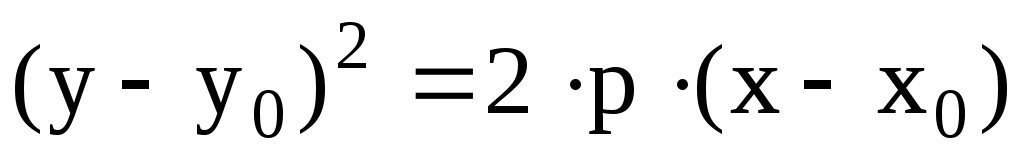 . (3.43) . (3.43)
3.7.4. Пара пересекающихся прямых
Уравнение  определяет пару пересекающихся прямых. Действительно, если этому уравнению удовлетворяет какая-либо точка M(x, y), то она удовлетворяет одному из уравнений определяет пару пересекающихся прямых. Действительно, если этому уравнению удовлетворяет какая-либо точка M(x, y), то она удовлетворяет одному из уравнений 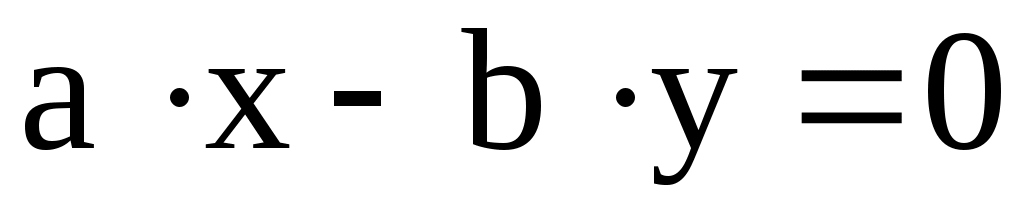 или или 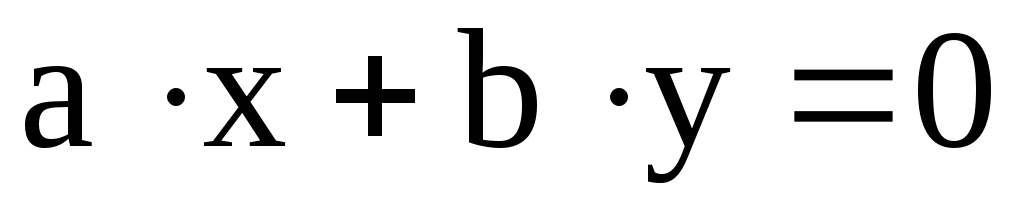 , или обоим этим уравнениям. , или обоим этим уравнениям.
3.8. ЗАДАЧИ
1. Написать каноническое уравнение эллипса и построить его:
а) 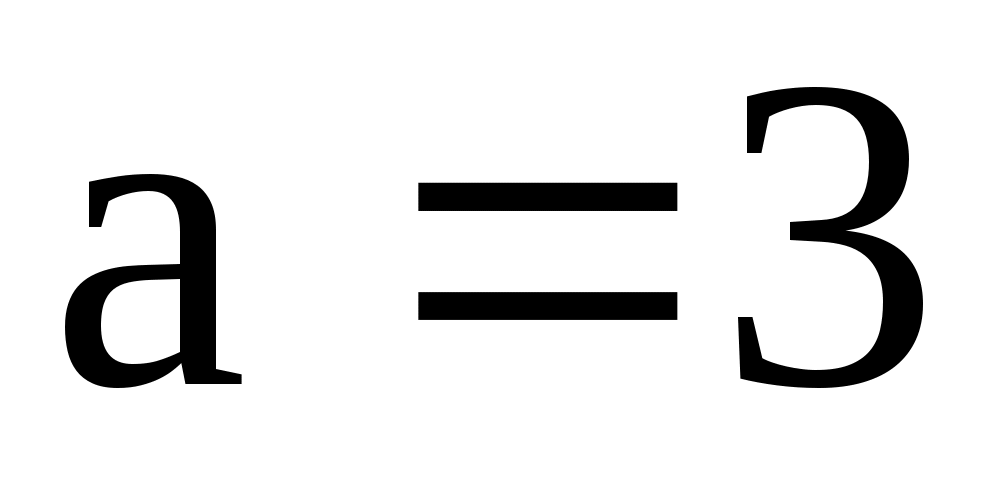 , , 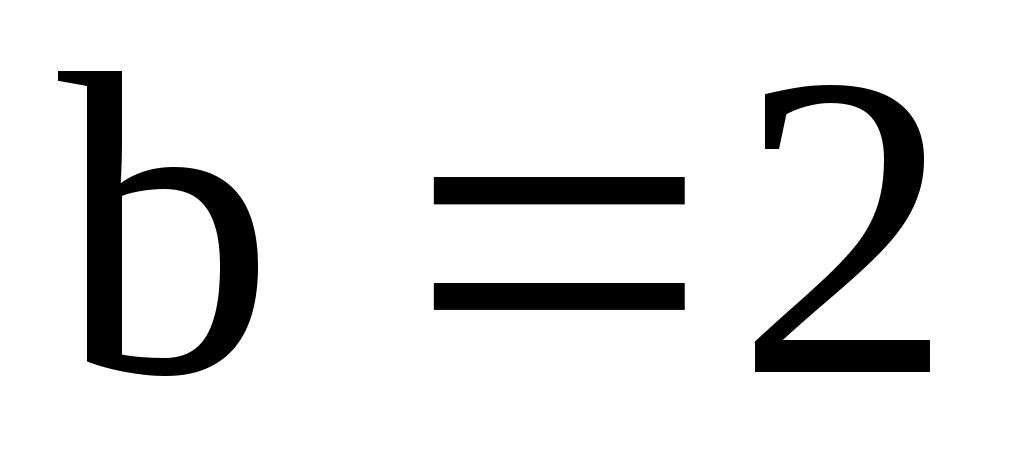 ; б) ; б) 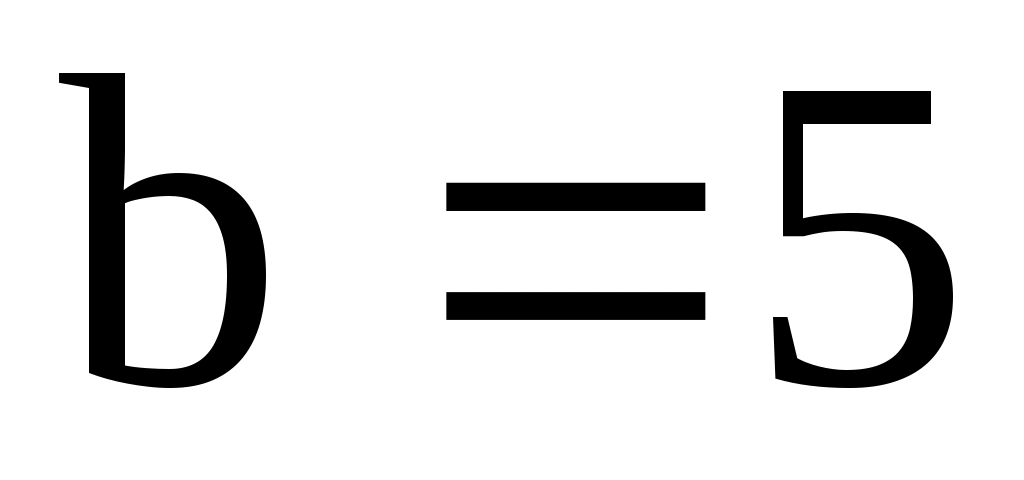 , , 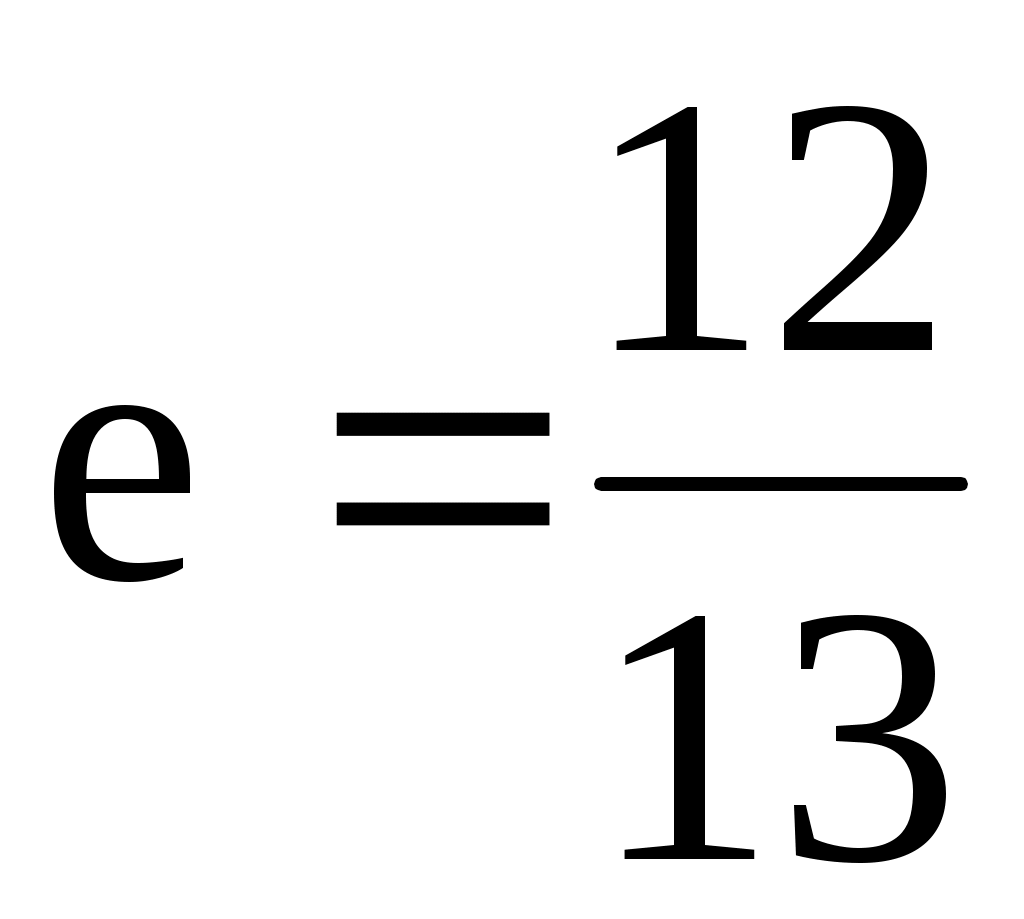 ; ;
в)  , расстояние между директрисами равно 5. , расстояние между директрисами равно 5.
2. Установить, что уравнение определяет эллипс (или окружность); найти его центр, полуоси, эксцентриситет, уравнения директрис; изобразить эллипс на координатной плоскости:
а) 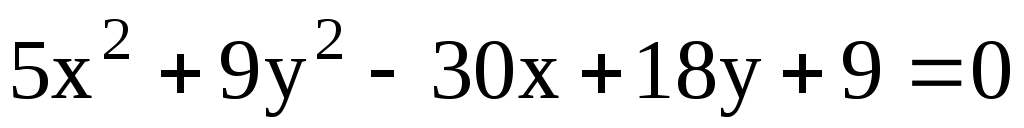 ; б) ; б) 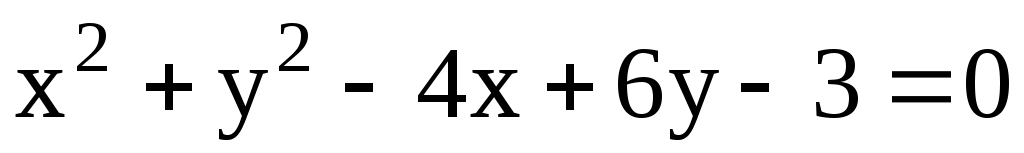 . .
3. Составить уравнение окружности, изобразить ее на координатной плоскости  , если: , если:
а) центр окружности находится в точке С(2;-3) и радиус равен 7;
б) окружность проходит через точку А(2;6), а ее центр находится в точке С(-1;2);
в) окружность проходит через три точки А(1;1), В(1;-1), D(2;0).
4. Написать каноническое уравнение гиперболы и построить ее:
а) 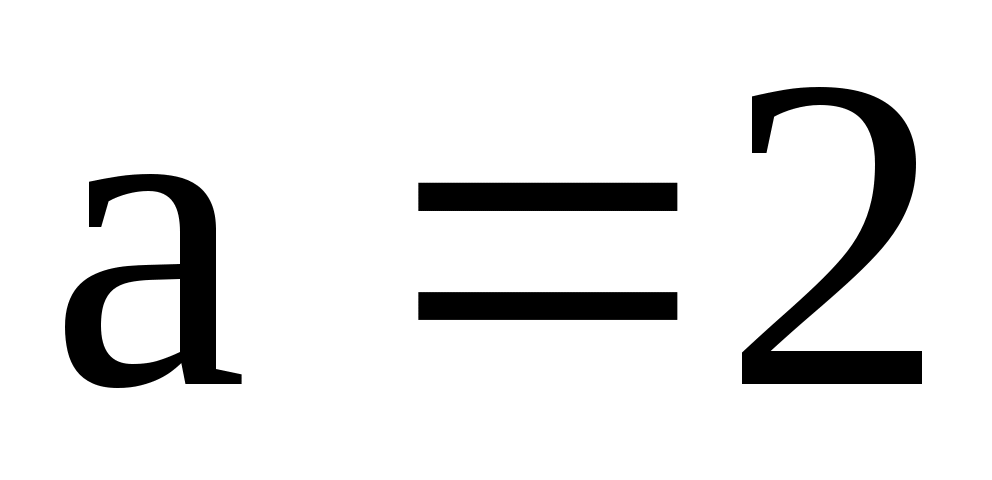 , , 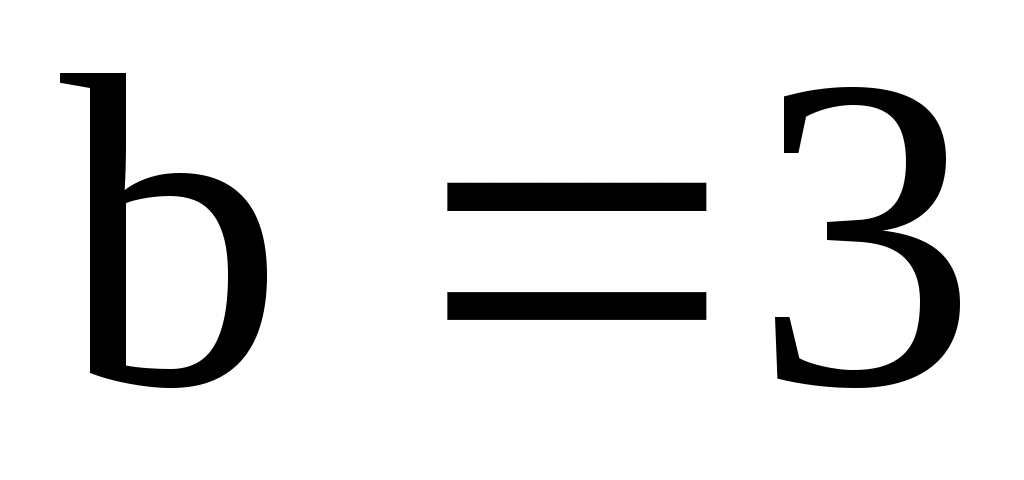 ; б) ; б)  , , 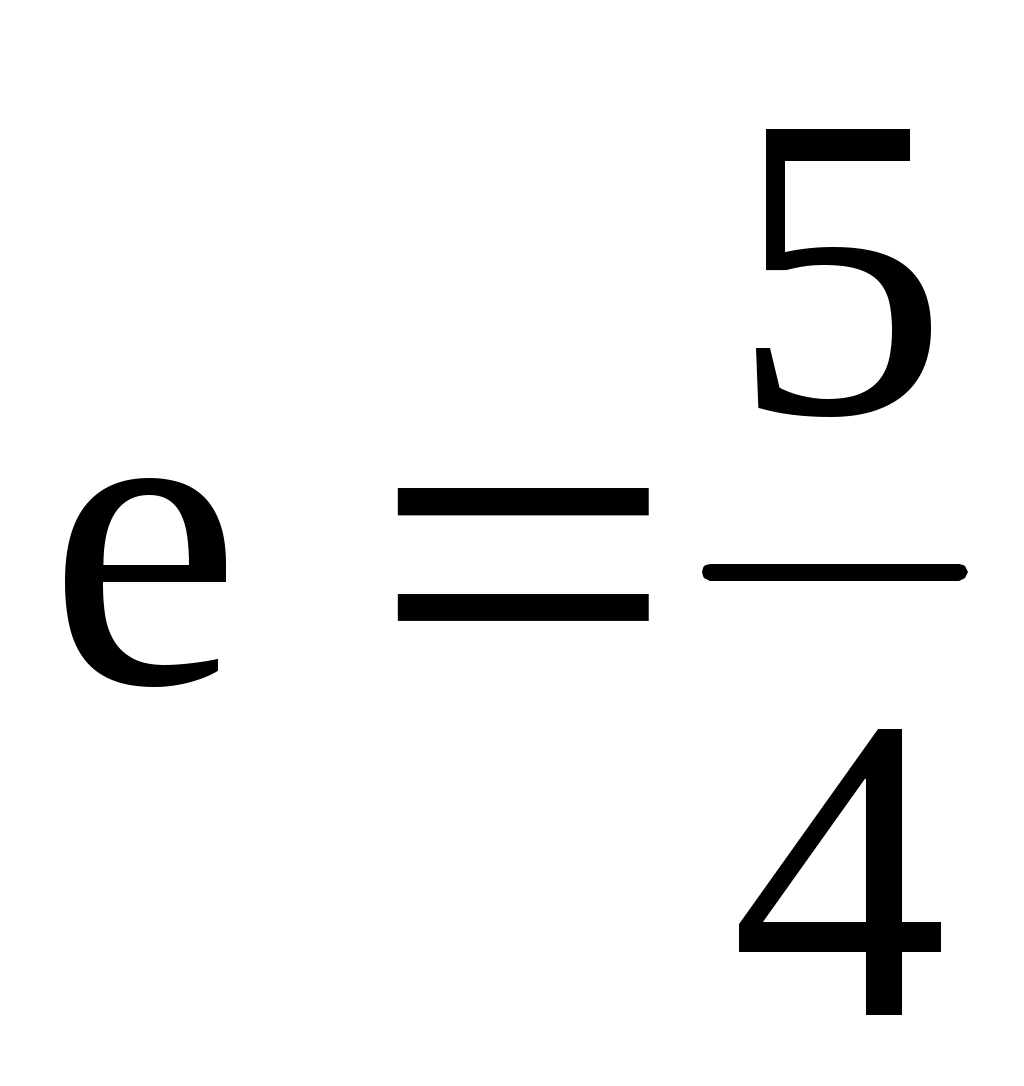 ; ;
в) 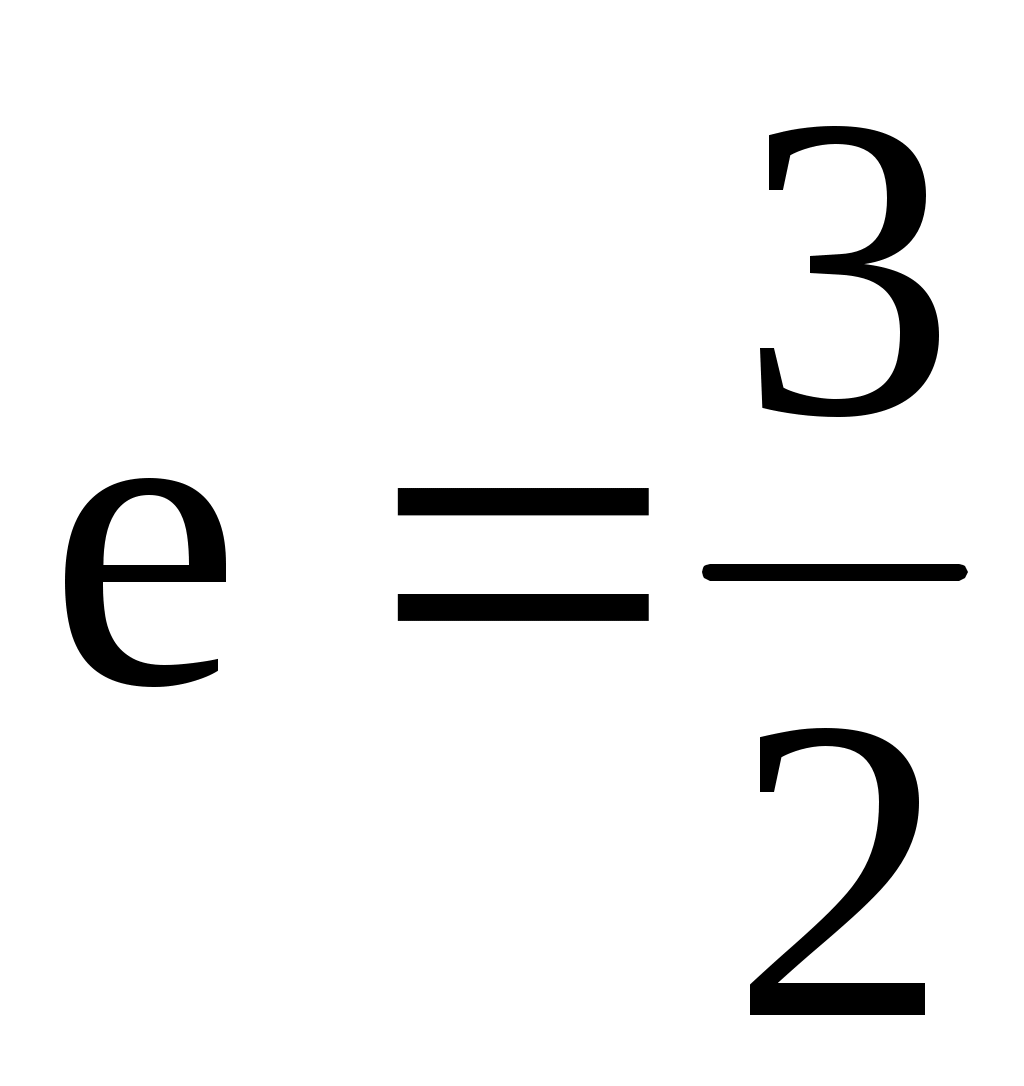 , расстояние между директрисами равно , расстояние между директрисами равно 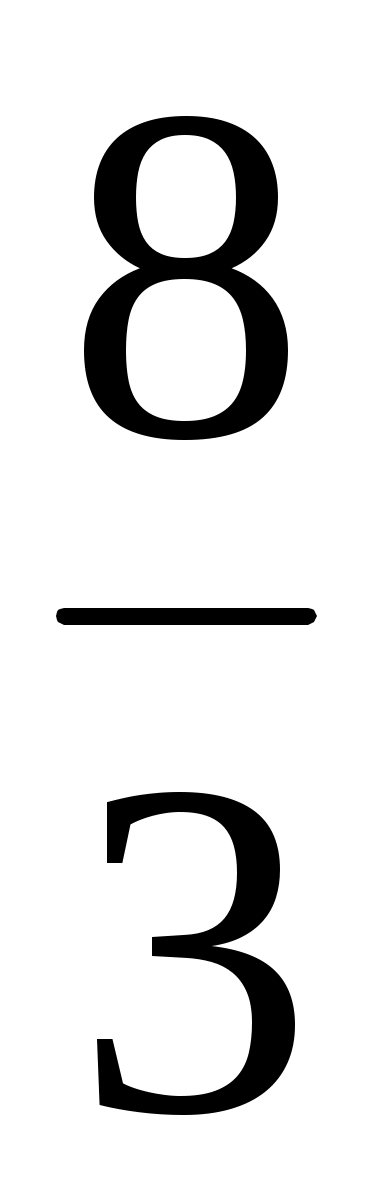 . .
5. Установить, что уравнение определяет гиперболу; найти ее центр, полуоси, эксцентриситет, уравнения директрис и асимптот; изобразить гиперболу на координатной плоскости: 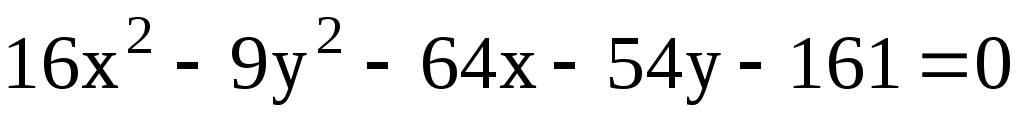 . .
6. Написать уравнение параболы с вершиной в начале координат, если:
а) парабола расположена в левой полуплоскости, симметрична относительно оси  и имеет параметр и имеет параметр 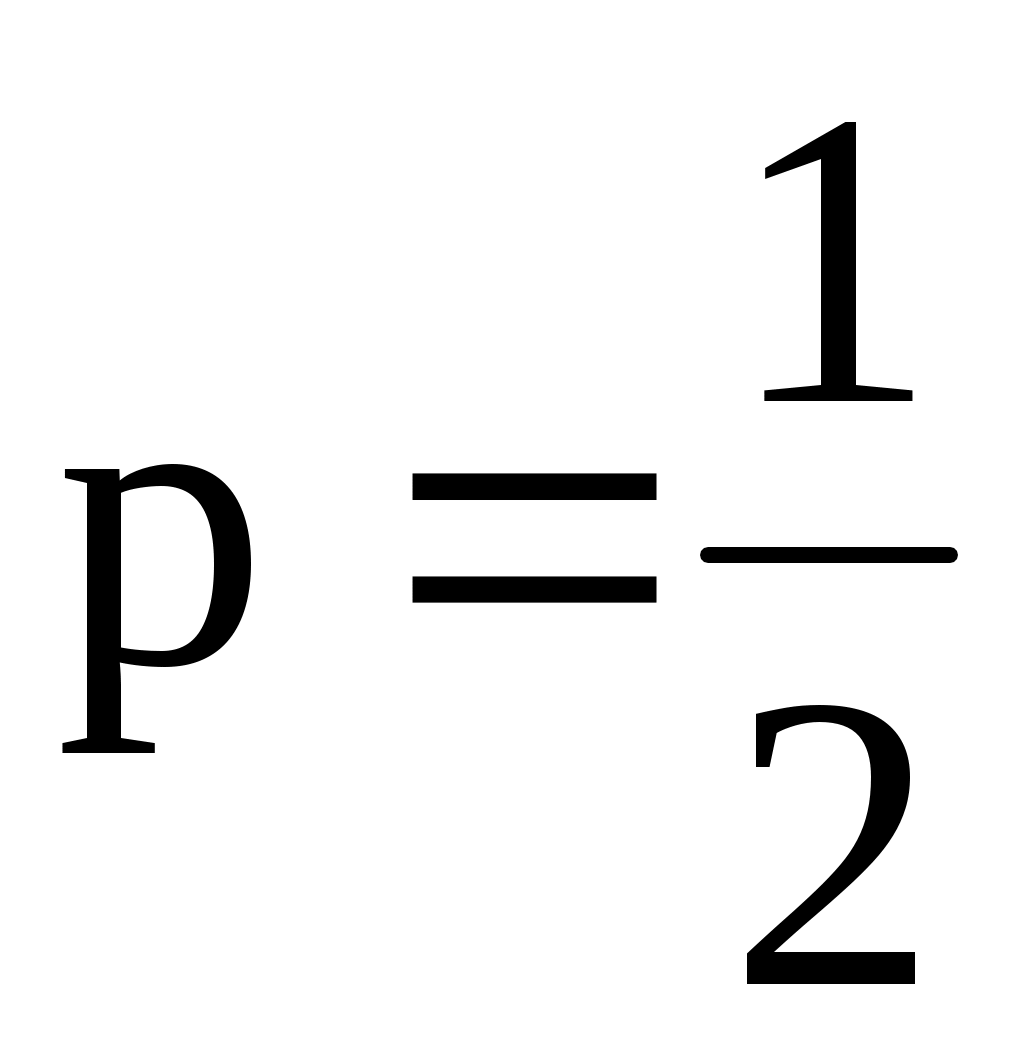 ; ;
б) фокус параболы находится в точке 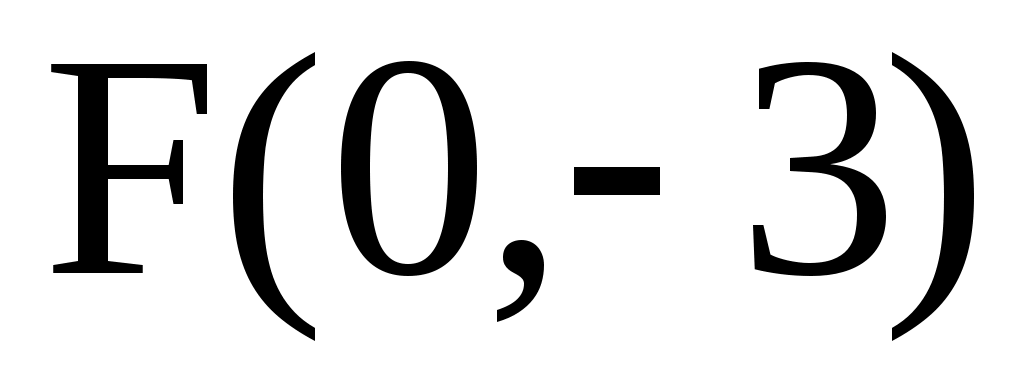 , а осью симметрии является ось , а осью симметрии является ось  . .
7. Установить, что уравнение определяет параболу, найти ее параметр, координаты вершины, уравнение директрисы; построить график:
а) 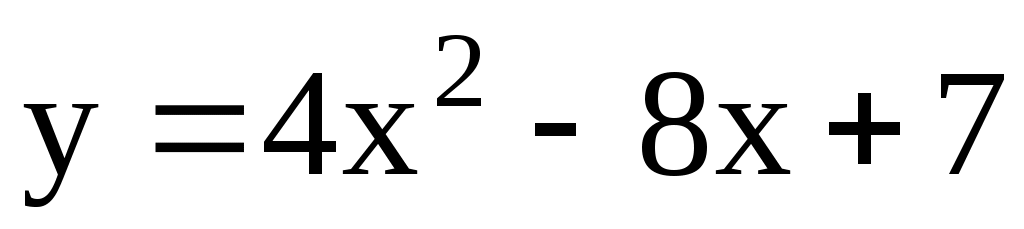 ; б) ; б) 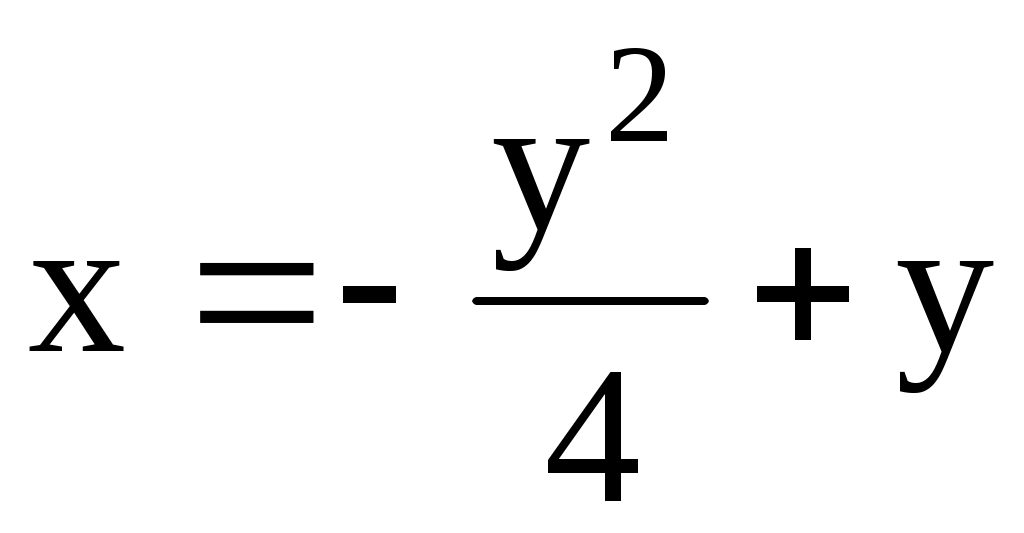 . .
8. Дан эллипс 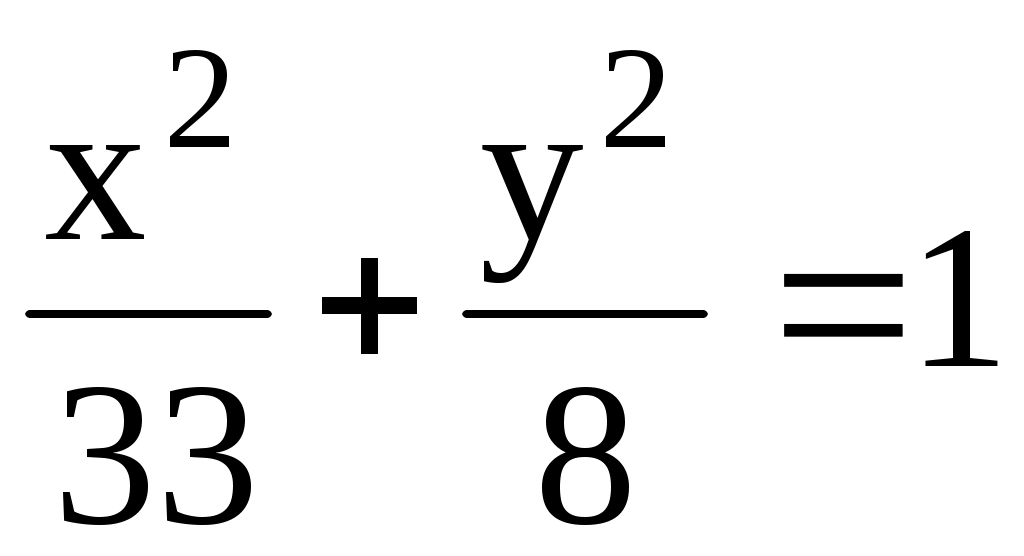 . Найти гиперболу, у которой фокусы совпадают с фокусами эллипса и эксцентриситет равен 1.25. . Найти гиперболу, у которой фокусы совпадают с фокусами эллипса и эксцентриситет равен 1.25.
|
|
|
 Скачать 1.38 Mb.
Скачать 1.38 Mb.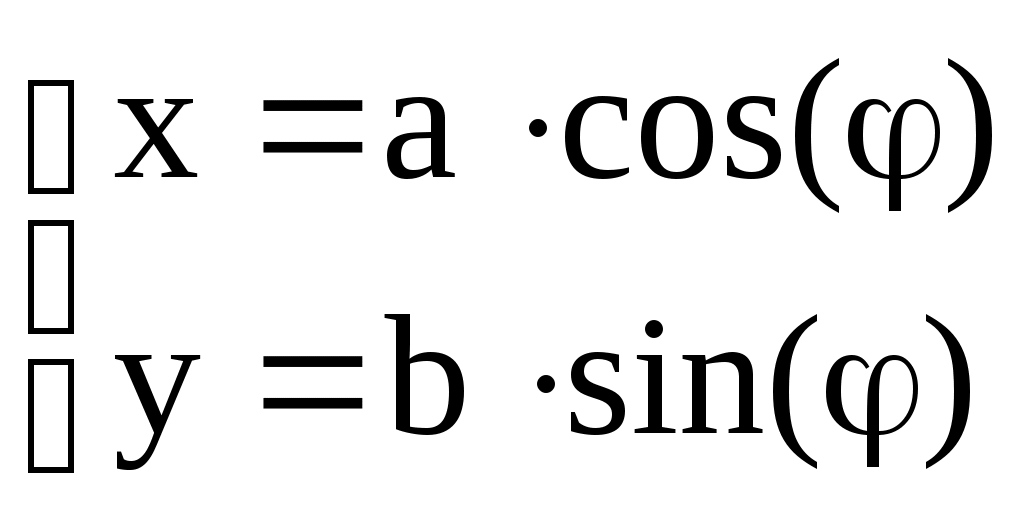 ,
, 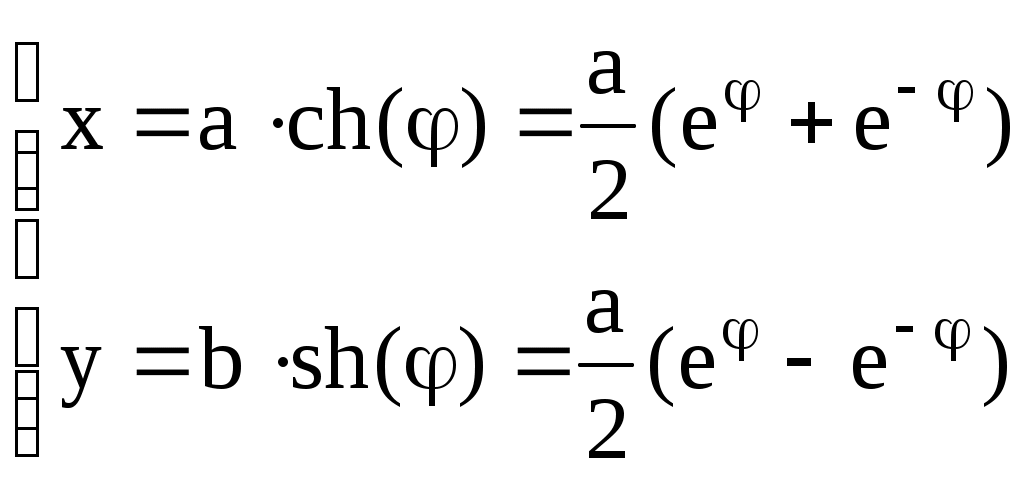 , (3.40)
, (3.40)