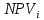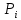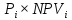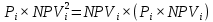201-204 Борисова. Анализ инвестиционных проектов, поддающихся дроблению
 Скачать 50.81 Kb. Скачать 50.81 Kb.
|
 Глава 30 Глава 30АНАЛИЗ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ, ПОДДАЮЩИХСЯ ДРОБЛЕНИЮ Рассматриваются инвестиционные проекты. Допускается, что можно реализовать не только целиком каждый из анализируемых инвестиционных проектов, но и любую его часть. При этом берется к рассмотрению соответствующая доля инвестиций и денежных поступлений. Возникает вопрос о максимизации отдачи на инвестированный капитал. Последовательность возможных действий такова:   приведенная стоимость денежных поступлений индекс рентабельности 1) для каждого инвестиционного проекта вычисляется индекс рентабельности по следующей формуле:  приведенная стоимость денежных оттоков = : ; 2) инвестиционные проекты, индекс рентабельности которых меньше единицы, следует отвергнуть; 3) инвестиционные проекты упорядочиваются по убыванию индекса рентабельности; 4) те первые инвестиционные проекты, которые могут быть профинансированы в полном объеме, реализуется. 5) очередной проект финансируется по остаточному принципу (лишь в той части, в которой он может быть профинансирован). Пример 88. Предприятие имеет возможность инвестировать 2,5 млн. руб. Рассматриваются следующие инвестиционные проекты, поддающиеся дроблению (денежные поступления со знаком «+», денежные оттоки со знаком «-»): A (-2; 0,7; 0,8; 1,1), В (-1,9; 0,6; 0,9; 1,2) и С (-1,7; 0,5; 0,7; 1,9). Альтернативные издержки по инвестициям равны 12%. Определим оптимальный инвестиционный портфель. Найдем индекс рентабельности каждого инвестиционного проекта. Для инвестиционного проекта А индекс рентабельности = (приведенная стоимость денежных поступлений)/(приведенная стоимость денежных оттоков) = (0,7/1,12 + 0,8/1,122 + 1,1/1,123)/2 ≈ 1,023. Для инвестиционного проекта В индекс рентабельности = (приведенная стоимость денежных поступлений)/(приведенная стоимость денежных оттоков) = (0,6/1,12 + + 0,9/1,122 + 1,2/1,123)/1,9 ≈ 1,109. Для инвестиционного проекта С индекс рентабельности = (приведенная стоимость денежных поступлений)/(приведенная стоимость денежных оттоков) = (0,5/1,12 + 0,7/1,122 + 1,9/1,123)/1,7 ≈ 1,386. Для всех инвестиционных проектов индекс рентабельности больше единицы. Ранжируем инвестиционные проекты по убыванию индекса рентабельности: С (1,386), В (1,109) и А (1,023). Так как предприятие имеет возможность инвестировать только 2,5 млн. руб., то проект С будет профинансирован полностью, а проект В - лишь частично на 2,5 (общая сумма) - 1,7 (инвестиции в проект C) = 0,8 млн. руб. Задача 88. Предприятие имеет возможность инвестировать 3 млн. руб. Рассматриваются следующие инвестиционные проекты, поддающиеся дроблению (денежные поступления со знаком «+», денежные оттоки со знаком «-»): A (-1,9; 0,8; 0,9; 1,2), В (-2,1; 0,7; 1,1; 1,3) и С (-1,6; 0,5; 0,8; 1,4). Альтернативные издержки по инвестициям равны 11%. Определить оптимальный инвестиционный портфель.  Глава 31 Глава 31 ДЕРЕВО ВЕРОЯТНОСТЕЙ ИНВЕСТИЦИОННОГО ПРОЕКТА Очень часто на практике возникают задачи изучения вероятностного распределения возможных чистых приведенных стоимостей инвестиционного проекта. Мы рассмотрим простой и наглядный подход к анализу таких распределений - дерево вероятностей инвестиционного проекта. Дерево вероятностей инвестиционного проекта рисуют слева направо. Места появления исходов обозначают в виде кругов, а каждый исход - сплошной линией (ветвью), идущей от соответствующего круга. Под каждой ветвью указывается вероятность соответствующего исхода, а над ветвью - денежные поступления или оттоки. Сумма вероятностей на ветвях, выходящих из одного круга, равна единице. Оценка вероятностей результатов инвестиционного проекта - простой метод оценки рисков капиталовложений. Этот метод требует, чтобы человек, принимающий инвестиционные решения, мог предвидеть множество возможных результатов инвестиционного проекта и был в состоянии оценить вероятность наступления каждого из возможных вариантов. Зная альтернативные издержки по инвестициям, определим для каждой возможной серии потоков денежных средств чистую приведенную стоимость NPVi (i = 1, 2, …, m). Здесь m - общее число возможных серий потоков денежных средств. Перемножив вероятности под ветвями, мы получим Pi - вероятность появления соответствующей серии потоков денежных средств (i = 1, 2, …, m). Тогда математическое ожидание вероятностного распределения возможных чистых приведенных стоимостей инвестиционного проекта равно 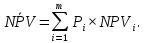 Дисперсия вероятностного распределения возможных чистых приведенных стоимостей инвестиционного проекта равна 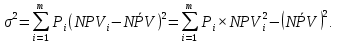 Стандартное отклонение вероятностного распределения возможных чистых приведенных стоимостей инвестиционного проекта равно 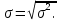 Пример 89. Первоначальные инвестиции равны 2,5 млн. руб. Дерево вероятностей инвестиционного проек- та имеет следующий вид (денежные суммы указаны в млн. руб.). 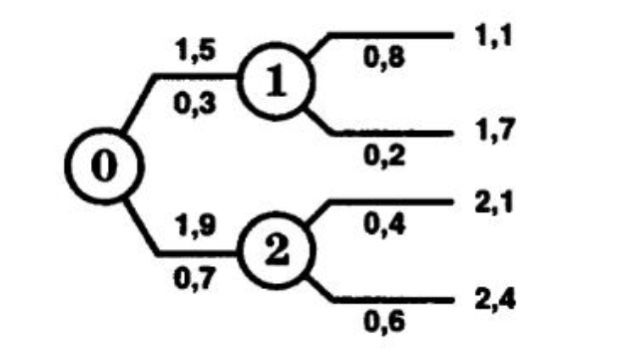 Альтернативные издержки по инвестициям равны 12%. Определим математическое ожидание и стандартное отклонение вероятностного распределения возможных чистых приведенных стоимостей инвестиционного проекта. Общее число возможных серий потоков денежных средств равно т = 4. Определим для каждой возможной серии потоков денежных средств чистую приведенную стоимость (i = 1, 2, 3, 4). NPV1 = 1,5/1,12 + 1,1/1,122 - 2,5 ≈ -0,28 млн. руб. NPV2 = 1,5/1,12 + 1,7/1,122 - 2,5 ≈ 0,19 млн. руб. NPV3 = 1,9/1,12 + 2,1/1,122 - 2,5 ≈ 0,87 млн. руб. NPV4 = 1,9/1,12 + 2,4/1,122 - 2,5 ≈ 1,11 млн. руб. Заполним таблицу.
Поясним, как заполняется таблица. В первых трех столбцах указаны номер возможной серии потоков денежных средств, чистая приведенная стоимость возможной серии и вероятность появления возможной серии соответственно. 4-й столбец - это произведение 2-го и 3-го столбцов. Числа 2-го столбца умножаем на числа 4-го столбца, результат округляем до трех цифр после запятой и пишем в 5-м столбце. В последней строке указана сумма чисел соответствующего столбца. Математическое ожидание вероятностного распределения возможных чистых приведенных стоимостей инвести- |