регресионный анализ. Эпид.2 сем. Анализ структуры и уровня заболеваемости. Определим интенсивный показатель для каждого исследуемого год
 Скачать 212.98 Kb. Скачать 212.98 Kb.
|
|
2.1. Определение прямолинейной тенденции многолетней динамики заболеваемости методом наименьших квадратов. Выявление резко отличающихся величин в динамическом ряду. Необходимость исследования динамических рядов с целью выявления и замены резко отличающихся показателей заболеваемости связано с тем, что такие показатели формируются, как правило, под действием случайных факторов, не характерны для основной части совокупности и могут привести к существенным искажениям многолетней тенденции заболеваемости. Показатели ранжируются, крайние члены ряда проверяются по критерию Шовене на “выскакивающие величины”. С этой целью рассчитывается средний многолетний показатель заболеваемости по формуле: Yср = ∑Yi/n, где Yi– показатель заболеваемости для каждого года, n – число лет исследования. Yср = 281,99/11 = 26 Расчет отклонений показателей заболеваемости от среднемноголетнего уровня, квадрат отклонений по формулам: (Y1-Yср); (Y1-Yср)²; ∑(Y1-Yср)² Данные заносятся в таблицу. Табл. 2.2.
Рассчитывается среднее квадратическое отклонение (δ) и ошибка (m) по формуле: δ = √3305,9/11 = 17,3, и Показатели прямолинейной тенденции вычисляются по формуле Y1 = a + bx. а – среднемноголетний уровень заболеваемости, m = δ√n-1 = 17,3/3,1=5,5 Табл. 2.3. Исходные материалы для изучения многолетней динамики заболеваемости Гриппом в Самарской области.
Далее проверяют крайние значения (max, min) ряда. Kmax = Ymax-Yср/δ Кmax = (56,15-26)/17,3=1,7 Сравниваем полученную величину с критерием Шовене для n=11: по таблице коэф.=2,26. Так как Kmax больше табличного коэффициента 2,26, то это “выскакивающая” величина. Учитывая, небольшой анализируемый ряд (11 лет), “выскакивающий” показатель заменим теоретическим, вычисленным по формуле для замены максимальных показателей: Kmin=Ymin-Yср/δ Kmin=(0,09-26)/17,3= -1,4 Сравниваем полученную величину с критерием Шовене для n=11: по таблице коэф.=2,26 Поскольку Kmin не превышает табличного коэффициента, то минимальное значение заболеваемости не является выскакивающей величиной. bx – переменная величина, формирующая прямолинейную тенденцию. X – условная нумерация периодов (лет) a = ∑Y/n = 25,6 b = ∑Yi*X/∑X² = 0,4 Полученные результаты заполняются в таблицу. Таблица 2.3.
Полученные показатели наносят на график: многолетняя динамика заболеваемости Гриппом в Самарской области 2012-2022 гг. (выравнивание по функции y=a+bx) 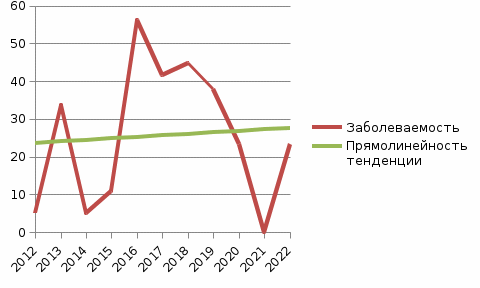 Рис 2.1. Заболеваемость Гриппом населения Самарской области за период 2012 – 2022 гг. Прямолинейная тенденция заболеваемости. Определяется общая направленность тенденции. Таким образом, при выравнивании динамического ряда методом наименьших квадратов выявляется тенденция к повышению заболеваемости. Вычисление криволинейной тенденции заболеваемости. Показатели криволинейной тенденции вычисляются по формуле Y2 = a+bx+cx² Получаем уравнение с 2-мя неизвестными: Y₂ = 25,6 + (0,4*x) + cx² Y₂ = 25,6+(0,4 *(-5) +25c Y₂= 25,6 + (-2)+25с Y₂ = 23,6 + 25c 23,6 = y - 25c y = 9,5 + 25c Определение выраженности тенденции Определяем средний абсолютный прирост, который характеризует среднюю величину ежегодного прироста или снижения заболеваемости по формуле: Δ = Yn – Y1 / n – 1; Yn - показатель заболеваемости последнего года, Y1 – показатель заболеваемости первого года, n – число анализируемых лет. Δ = 23,32 – 5,15/10=1,8 Рассчитываем среднемноголетний темп прироста (T пр.ср) для прямолинейной тенденции: Tпр.=B * 100%/A, где B- величина, на которую ежегодно идет прирост или снижение заболеваемости; A – среднемноголетний показатель заболеваемости. Tпр. = 1,8 * 100/25,6 = 7 Оценивается выраженность тенденции по следующим критериям: Tпр.ср. от 0 до ±1% - заболеваемость стабильна. Tпр.ср. от ±1 до ±5% - тенденция динамики заболеваемости умеренная (средневыраженная), Tпр.ср. ≥ ±5% - тенденция выраженная. Вывод: выраженность тенденции к повышению заболеваемости Гриппом в Самарской области за период 2012-2022 гг умеренная или средневыраженная. Сглаживание динамического ряда для оценки цикличности. Устранение действия случайных факторов методом укрупнения периодов Объединяем несколько смежных годов (2,3,4, и т.д.), рассчитываем для них среднюю величину заболеваемости по формуле: Yср =Y1 + Y2 + Y3 /3 Полученные значения заносим в таблицу (2.4) и строим график (2.2) Преобразование динамического ряда методом скользящей средней: точки теоретической линии также определяются как средние арифметические из показателей нескольких смежных лет, но каждый показатель учитывается при расчете нескольких средних. Например, при скользящем осреднении с шагом 3 года, скользящие средние определяются по формулам: Yср1 =Y1 + Y2 + Y3 /3; Yср2 =Y1 + Y2 + Y3 /3 На графике полученные значения откладываем, соответственно, напротив 2-го и 3-го года. Когда период осреднения включает четное число лет, скользящие средние относят к середине интервала между двумя центральными годами. Полученные данные вносим в таблицу (2.4) и строим график (2.3) Таблица 2.4.
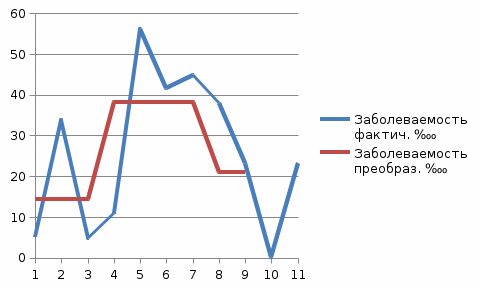 Рис. 2.2. Заболеваемость при преобразовании динамического ряда методом укрупнения периодов. 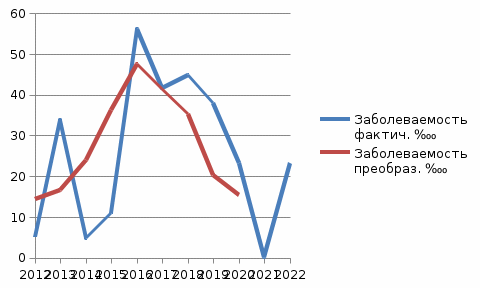 Рис. 2.3. Заболеваемость при преобразовании динамического ряда методом скользящей средней. Выводы: При преобразовании динамического ряда заболеваемости населения Гриппом методом укрупнения периодов и методом скользящей средней, на графиках преобразованные линии заболеваемости имеют такие же периоды снижения и повышения заболеваемости совокупного населения Гриппом Самарской области, как и на графике заболеваемости населения в динамике за период с 2012 по 2022 гг, и имеют 2 периода повышения заболеваемости: 2012 г. по 2013 г., и с 2014 г. по 2016 г; и 2 периода снижения заболеваемости: с 2017 г. по 2019 г., и с 2020 г. по 2022 г. с тенденцией к стабилизации заболеваемости. 2.2 Определение цикличности эпидемического процесса Проводится на основании оценки соотношения кривой фактической заболеваемости и прямолинейной тенденции. Определение эпидемических и межэпидемических лет в анализируемом периоде, т.е. цикличности в течение эпидемического процесса. Определяется разность между фактической заболеваемостью (Yфакт.) и теоретический (Yт.), рассчитанной для каждого года. Проводится выравнивание динамического ряда методом скользящей средней полученной разности по анализируемому ряду с шагом 2 года т.е, Y₁ = (Y факт 2000 - Y r2000) + (Y факт.2001 - Y +2001) /2 Y₂= (Y факт 2001 - Y (2001) + (Y факт 2002 - Y +2002) /2 Данные заносятся в таблицу. Таблица 2.5.
Строим график цикличности эпидемического процесса, где ось абсцисс – теоретически рассчитанная линия тенденции, а по оси ординат в верхнем и нижнем направлении откладываются значения разности между фактической заболеваемостью и теоретически рассчитанной по каждому анализируемому году. На полученный график наносятся сглаженные методом скользящей средней показатели заболеваемости. Определяем число циклов, сроки начала и окончания, продолжительность положительных (периоды подьёма) и отрицательных (периоды спада) фаз циклов за анализируемый период. 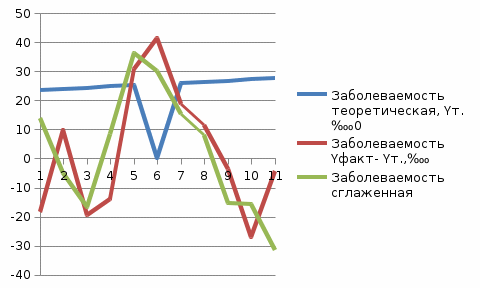 Рис. 2.4. График цикличности эпидемического процесса Гриппа в Самарской области за период с 2012 по 2022гг. Выводы: на полученном графическом изображений динамики заболеваемости населения Самарской области Гриппом, цикличность отсутствует. Также, на графике выражены периоды подъёма и снижения заболеваемости: за период с 2012 по 2022 гг, и имеют 2 периода повышения заболеваемости: 2012 г. по 2013 г., и с 2014 г. по 2016 г; и 2 периода снижения заболеваемости: с 2017 г. по 2019 г., и с 2020 г. по 2022 г. 2.3. Прогнозирование показателя заболеваемости на следующий год. Прогноз осуществляется по уравнению, наиболее близко описывающему тенденцию развития эпидемического процесса (Y₁= а + bx и Y₂=а + bx + cx²) путем присвоения условного номера X прогнозируемому году и решения соответствующего уравнения. Доверительный интервал прогнозируемого показателя определяется, как Y прог ±3 m. Ошибку прогноза можно рассчитать по формуле: m = √Y прог (100 000 - Y прог) / N, где N - ожидаемая численность населения в прогнозируемом году, 100 000 - размерность относительного показателя, Yпр= 25,6 + 0,4 * 5 = 27,6 m = √Yпр. (100 000 - Y пp) / N = √27,6 (100 000- 27,6)/1 000 000 = 1,6 Доверительный интервал (ДИ) = 27,6 ± 1,6 * 3 = 27,6±4,8 Вывод: прогнозируемый показатель заболеваемости населения Гриппом на следующий год составил 27,6 ± 4,8 2.4.Определение скрытой вспышечной заболеваемости Скрытая вспышечная заболеваемость определяется в годы с высоким уровнем заболеваемости, как разность между фактическим и предельным теоретическим показателем заболеваемости. Рассчитываем предельный теоретический уровень заболеваемости для каждого анализируемого года по формуле: Yпp=Ym + 3 m где Yпр - предельный теоретический показатель заболеваемости; Yт - теоретический уровень заболеваемости, рассчитанный по параболе 1-го или 2-го порядка; m - ошибка показателя. Число заболевших во вспышке (А) рассчитывается по формуле: A = N* Yвсп/ 100 000, где N - ожидаемая численность населения в прогнозируемом году, 100 000 - размерность относительного показателя. Yвсп - Y факт - Yпр где Yфакт - фактическая заболеваемость; Yпр - предельный теоретический показатель заболеваемости. Yпp = Ym + 3m где Ym - теоретический уровень заболеваемости, рассчитанный по параболе 1-го или 2-го порядка; m = √ Y пp. (100 000 - Yпp) / N
Вывод: в 2013 году число заболевших людей во вспышке составило 157 человек, в 2016 году – 837,7 человек, в 2017 г. – 1174,8 человек, в 2018 году – 449,4 человек, в 2019 году – 216,1 человек. В остальные анализируемые годы, значения со знаком минус свидетельствуют о количестве предотвращенных случаев заболевания в годы со сравнительно низким уровнем заболеваемости. Абсолютные числа заболеваемости Гриппом по месяцам в Самарской области за период 2012 по 2022 годы.
Численность населения г. Самара за 2012-2022 г.г.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
