Автоматизированные системы управления атомных электростанций 2

• Название: Автоматизированные системы управления атомных электростанций 2
• Анкор: Ekzamen_I_Kollokvium.docx
• Дата: 06.03.2018
• Размер: 1.06 Mb.
• Имя файла: Ekzamen_I_Kollokvium.docx
• Тип: Документы; #16306
• страница: 29 из 40

Классификация объектов тепловой энергетики по параметру регулирования и их математическое описание.

Если в основу классификации положить параметр регулирования, то объекты регулирования тепловой энергетики можно подразделить на несколько групп, каждая из которых, в качестве регулируемого параметра соответственно имеет угловуюскорость вращения ротора, давление газа или пара в ресивере, уровень жидкости в резервуаре, температуру в камере и т.д.

Каждая из этих групп регулируемых объектов описываетсяоднотипными уравнениями движения.

Первая группа. Равновесный режим работы объектов, отнесенных к данной группе, обеспечивается равенством крутящего момента М_д0, вырабатываемого машиной на равновесном режиме моменту М_с0потребителя (сопротивления) на этом же режиме!

Уравнение равновесного состояния (уравнение статики) таких объектов имеет вид

М_д0 = М_с0.(34)

Нарушение равновесного состояния, например в связи с изменением нагрузки, приводит к появлению разницы в значениях крутящих моментов машины и потребителя. Отклонение объекта от равновесного состояния вследствие изменения указанных моментов отражается в уравнении динамики объекта. Разница моментов расходуется на ускоренное или замедленное вращение ротора, поэтому



где J— приведенный момент инерции ротора объекта,

принимаемый постоянным; (£> — угловая скорость (выходная координата объекта); М_ди М_с— измененные значения моментов двигателя и потребителя.

Вторая группа. Объекты, относящиеся ко второй группе, представляют собой ресивер определенного объема с коммуникациями подвода и отвода газа.

Уравнение статики таких объектов получает вид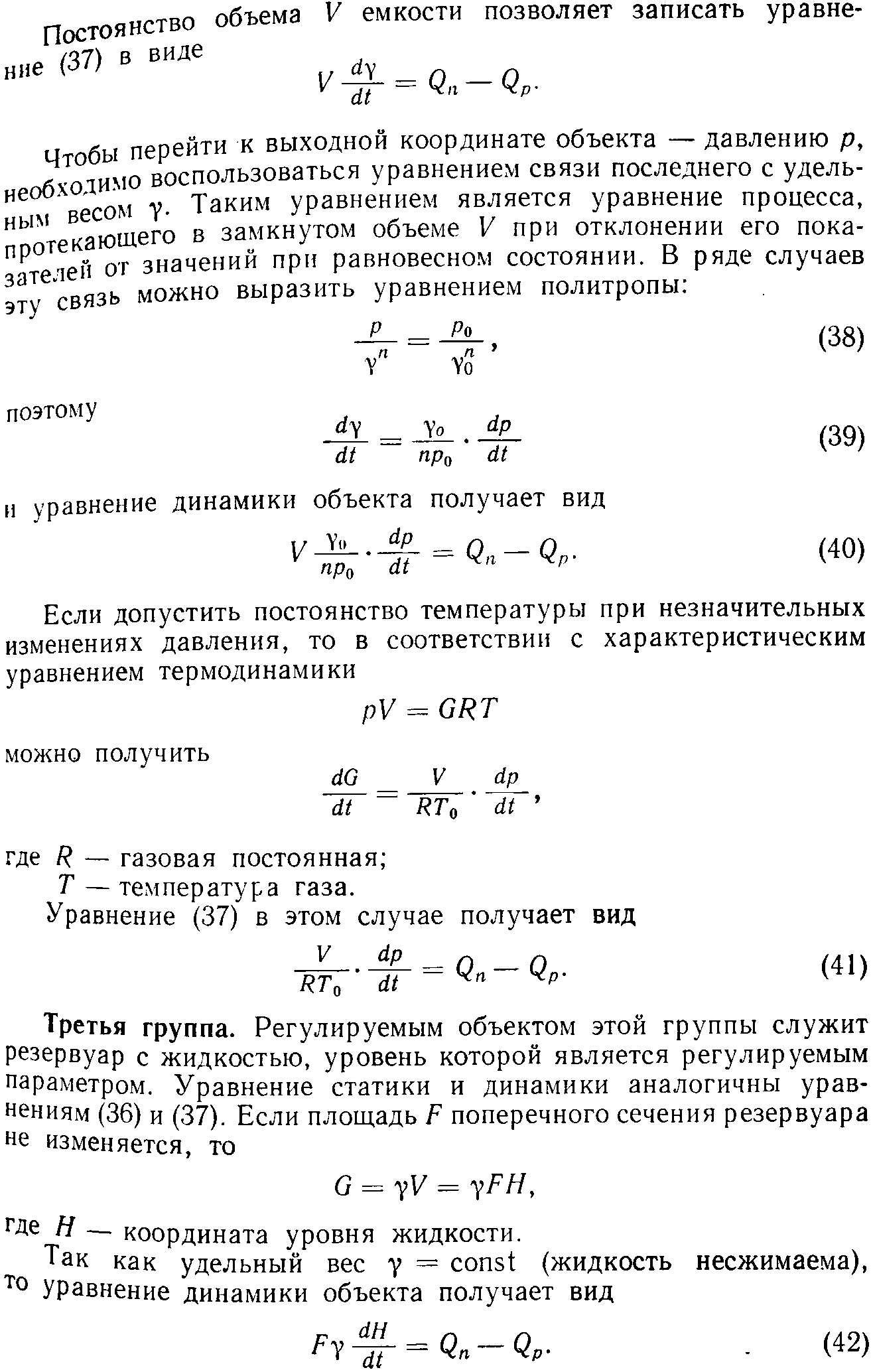





Четвертая группа. Регулируемым объектом этой группы может быть камера, в которой необходимо поддерживать заданное значение температуры. Условие равновесного состояния объекта (уравнение статики) — равенство (на равновесном режиме) подводимого и отводимого тепла



Если равновесное состояние нарушено, то уравнение динамики позволяет определить количество тепла, аккумулируемое в данной камере: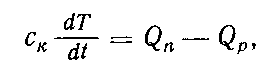



где с_к — теплоемкость камеры в ккал/град.

Приведенные выше уравнения динамики регулируемых объектов однотипны и легко подчиняются обобщенной энергетической форме: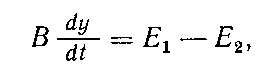



где — аккумулируемая в данном объекте энергия;

В — постоянная объекта; у — регулируемый параметр; Е_ги E₂ — подводимая и отводимая энергии.

3. Общий вид экспериментальных переходных кривых теплоэнергетических процессов. Обобщенная энергетическая форма уравнений динамики регулируемых объектов.

Особенностью реального управления многими инерционными технологическими процессами, такими как процесс регулирования давления, расхода, уровня, температуры, является апериодичность переходных характеристик.

Увеличение количества емкостей, составляющих регулируемый объект, приводит, очевидно, к соответствующему увеличению порядка дифференциального уравнения, описывающего процесс разгона для регулируемой величины в последней из емкостей при возмущении на входе в объект

Переходный процесс многоемкостного теплового регулируемого объекта за редким исключением описывается дифференциальными уравнениями, характеристические уравнения которых имеют лишь действительные корни. Поэтому процессы разгона в них протекают апериодически, а их кривые разгона являются суммами экспонент (рис. III. 8, кривые 2, 3, 4) и имеют характерную «S-образную» форму. Чем больше составляющих емкостей имеет регулируемый объект при прочих равных условиях, тем более полого идет кривая разгона в начале процесса и тем длительнее его течение (кривые 3 и 4 рис. III. 8). При отсутствии самовыравнивания в регулируемом объекте форма кривых разгона будет несколько иной (рис./III. 9). В этом случае любая из кривых будет уходить в бесконечность, становясь, при достаточном удалении от начала процесса, прямолинейной.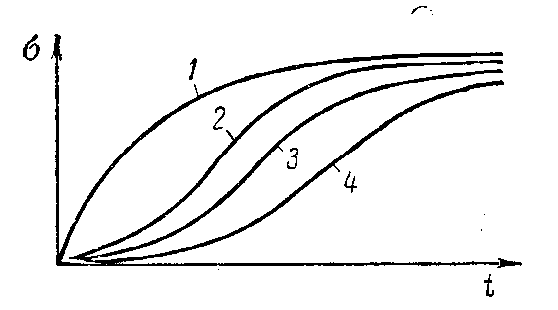



Рис. III. 8. Характеристики разгона многоемкостных объектов при наличии самовыравнивания. Цифры на рисунке соответствуют числу емкостей объекта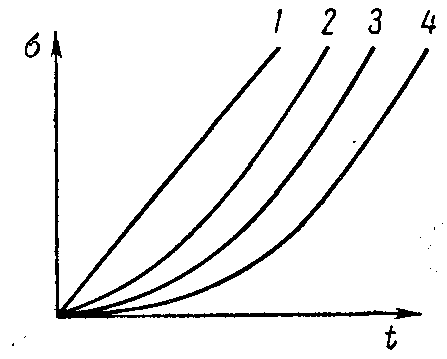



Рис. III. 9. Характеристики разгона многоемкостных объектов в отсутствии самовыравнивания. Цифры на рисунке соответствуют числу емкостей объекта

Общий вид экспериментальных переходных кривых таких процессов характеризуется тремя основами параметрами: Т, г, V — постоянной времени, временем отставания и скоростью нарастания соответственно, а простейшей обобщенной моделью является модель.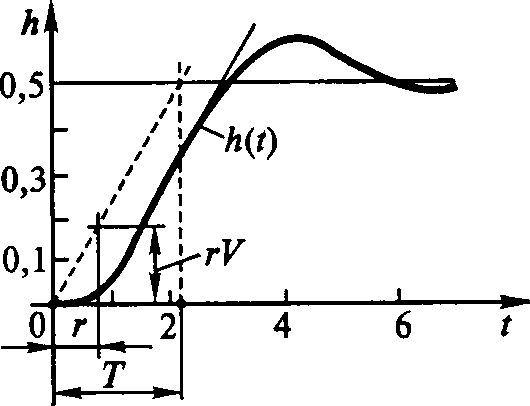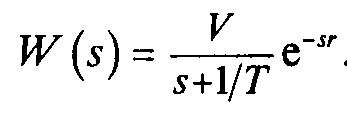



Если к кривой разгона многоемкостного объекта (рис. III. 12) провести касательную в точке ее перегиба (или в бесконечности в случае отсутствия самовыравнивания рис. III. 13), то эта касательная отсечет на оси времени некоторый отрезок, обозначаемый т_е и называемый емкостным запаздыванием. Из кривых рис. III. 8, III. 9 легко видеть, что емкостное запаздывание при прочих равных условиях тем больше, чем большее число емкостей составляет регулируемый объект. В точке перегиба (или в бесконечности для объектов, лишенных самовыравнивания) скорость изменения регулируемой величины является наибольшей. Следовательно, в соответствии с определением скорости разгона, данной в § 1 и 3, скорость разгона многоемкостного регулируемого объекта может быть определена по углуа наклона касательной в точке перегиба к кривой разгона.

Конечное отклонение регулируемой величины о_копределяется степенью самовыравнивания регулируемого объекта и равна ее обратной величине при единичном ступенчатом возмущении. Таким образом, течение процесса разгона многоемкостного регулируемого объекта, а, следовательно, и его кривая разгона приближенно характеризуются тремя величинами — скоростью разгона е, степенью самовыравнивания q и величиной времени емкостного запаздывания т_е.

В очень большом числе случаев в тепловых регулируемых объектах имеет место так называемое чистое или транспортное запаздывание т₀. Оно обусловливается тем, что с момента нанесения возмущения и до того момента, когда регулируемая величина начнет изменяться, должно пройти некоторое время, затрачиваемое на перемещение регулируемой среды от места нанесения возмущения до места измерения регулируемой величины. Это явление хорошо видно на гидравлической модели одноемкостного объекта с запаздыванием (см. рис. II. 20),

При регулировании уровня воды в баке (рис. II. 20) возмущение в виде изменения подачи воды на стороне притока изменяет подачу воды в открытый желоб, по которому вода и подается в бак. Время запаздывания здесь зависит от длины и наклона желоба.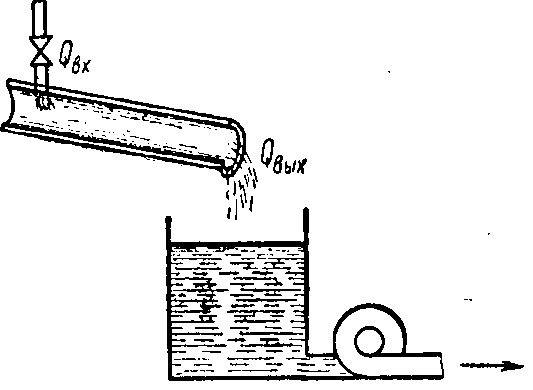

Рис. II. 20. Конструктивная схема запаздывающего звена

Таким образом, типовая характеристика разгона сложного (многоемкостного) теплового регулируемого объекта имеет характерный вид, изображенный на рис. III. 12 и III. 13. Сумма транспортного и емкостного запаздываний

т₀ + т_е = т (III. 11)

называется полным или условным запаздыванием.

Подводя итоги, мы можем отметить следующие основные особенности сложных тепловых регулируемых объектов:

а) процессы разгона в подавляющем большинстве сложных тепловых регулируемых объектов протекают апериодически и, следовательно, их разгонные характеристики монотонны;

б) колебания, проходя через тепловые регулируемые объекты, отстают по фазе от входных колебаний и уменьшаются по своей амплитуде по мере возрастания их частоты;

в) амплитудно-фазовые характеристики тепловых регулируемых объектов в комплексной плоскости представляют собой спирали, закручивающиеся около начала координат, т. е. около точки, соответствующей бесконечно большой частоте колебаний;

г) тепловые регулируемые объекты являются низкочастотными фильтрами и не пропускают практически колебаний, у которых частота равна или больше некоторой частоты среза со_ер;

д) подавляющее большинство сложных тепловых объектов обладает кроме емкостного также и транспортным запаздыванием.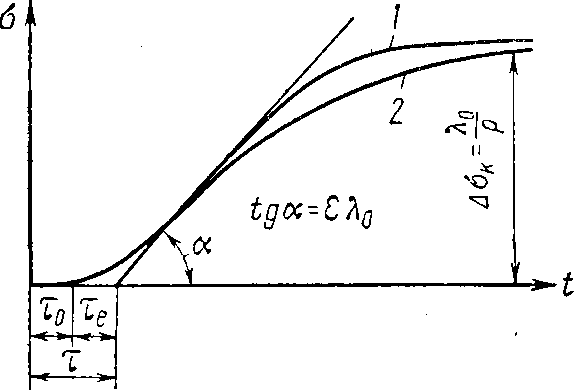



Рис. III. 12..Кривая разгона сложного объекта с самовыравниванием / и аппроксимация ее апериодическим звеном с транспортным запаздыванием т, равным сумме емкостного т_е и действительного транспортного т₀ запаздываний.