Экономико-статистический отраслевой анализ рынка. Автомобильный. Бакалаврская работа Экономикостатистический анализ отраслевой организации рынков
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
Анализ изменений структуры.Структура – взаимное расположение групп, связи между которыми определяют специфику изучаемой совокупности. Структуру совокупности можно исследовать по распределению признака. Признак может измеряться в любой шкале. Предпочтительно измерение в качественной шкале. Цель структурного анализа – описать закономерности формирования совокупности исследуемых единиц: провести типологизацию элементов, выделить приоритетные, доминантные и малозначимые единицы. Существует две группы показателей для измерения структуры и различий структуры: индивидуальные: доля, накопленная доля, абсолютное изменение доли, относительное изменение доли, коэффициенты координации, коэффициенты нагрузки; обобщающие: а) характеристики свойств одной структуры (экстремальные значения, средний уровень, характер вариации, форма распределения), б) обобщающие индексы сравнения двух структур во времени и пространстве, в) обобщающие индексы сравнения нескольких структур во времени и пространстве. В международной статистической практике наибольшее распространение получили такие обобщающие индексы сравнения двух и более структур, как линейный коэффициент абсолютных структурных сдвигов Казинца: 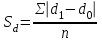 , где , где 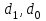 - удельные веса (выраженные в %) отдельных элементов совокупности в рассматриваемом и предыдущем периодах, n – число выделяемых элементов в совокупности; - удельные веса (выраженные в %) отдельных элементов совокупности в рассматриваемом и предыдущем периодах, n – число выделяемых элементов в совокупности;квадратический коэффициент абсолютных структурных сдвигов Казинца: 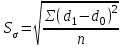 , где , где 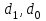 - удельные веса (выраженные в %) отдельных элементов совокупности в рассматриваемом и предыдущем периодах, n – число выделяемых элементов в совокупности. - удельные веса (выраженные в %) отдельных элементов совокупности в рассматриваемом и предыдущем периодах, n – число выделяемых элементов в совокупности. Линейный и квадратический коэффициенты абсолютных структурных сдвигов показывают: на сколько процентных пунктов в среднем отклоняются друг от друга рассматриваемые удельные веса. При отсутствии сдвигов коэффициенты принимают значение 0. Верхней границы эти коэффициенты не имеют. Чем больше изменилась структура, тем выше значения этих индексов. Из данных двух индексов предпочтительнее использовать квадратический, так как он более чувствителен к сильным колебаниям структуры. Для оценки существенности структурных изменений в относительном выражении в мировой аналитической практике наиболее широко используются интегральные индексы Салаи и Гатева. Эти индексы учитывают численность совокупности, количественный вклад групп в общий объем изучаемого признака. Обобщающие показатели структурных сдвигов позволяют проанализировать не только различия совокупностей, но и оценить динамику изменения структуры. Интегральный коэффициент структурных сдвигов Гатева позволяет учесть интенсивность изменений по отдельным группам и удельный вес этих групп в сравниваемых совокупностях: 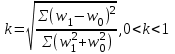 . .Интегральный коэффициент структурных различий Салаи позволяет учесть интенсивность изменений по отдельным группам, удельный вес этих групп в сравниваемых совокупностях, а также число групп: 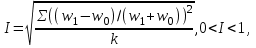 k- число групп. k- число групп.Методы классификации.При наличии нескольких признаков (исходных или обобщенных) задача классификации может быть решена методами кластерного анализа, которые от других методов многомерной классификации отличаются отсутствием обучающих выборок, то есть априорной информации о распределении генеральной совокупности, которая представляет собой вектор Х. После того, как сформулирована цель работы, необходимо определить критерии качества, целевую функцию, значения которой позволят сопоставить различные схемы классификации. Как правило, целевая функция должна минимизировать некоторый параметр (например, группировка, минимизирующая совокупность затрат и средств на ремонтные работы). Если формализовать цель не удается, то критерием качества классификации может служить возможность содержательной интерпретации найденных групп. Полученные в результате разбиения группы называются кластерами, а также таксонами. Методы нахождения кластеров называются кластер-анализом. Есть три различных подхода к проблеме кластерного анализа: эвристический (отсутствие формальной модели и критерия для сравнения), экстремальный (нет модели, но задается критерий, определяющий качество разбиения на кластеры), и статистический (есть вероятностная модель исследуемого процесса). Понятие однородности объектов задается либо введением правила вычисления расстояния 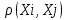 между любой парой исследуемых объектов (Х1,Х2…Хn), либо заданием некоторой функции r(Xi,Xj), характеризующей степень близости i-ого и j-ого объектов. Если задана функция между любой парой исследуемых объектов (Х1,Х2…Хn), либо заданием некоторой функции r(Xi,Xj), характеризующей степень близости i-ого и j-ого объектов. Если задана функция 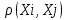 , то близкие с точки зрения этой метрики объекты считаются однородными, принадлежащими одному классу. Выбор метрики или меры близости является узловым моментом исследования, от которого в основном зависит окончательный вариант разбиения объектов на классы при данном алгоритме разбиения. Наиболее часто используемые расстояния и меры близости в задачах кластерного анализа: , то близкие с точки зрения этой метрики объекты считаются однородными, принадлежащими одному классу. Выбор метрики или меры близости является узловым моментом исследования, от которого в основном зависит окончательный вариант разбиения объектов на классы при данном алгоритме разбиения. Наиболее часто используемые расстояния и меры близости в задачах кластерного анализа:расстояние Махаланобиса 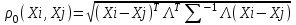 , где Λ-некоторая симметрическая неотрицательно-определенная матрица «весовых» коэффициентов, которая чаще всего выбирается диагональной. , где Λ-некоторая симметрическая неотрицательно-определенная матрица «весовых» коэффициентов, которая чаще всего выбирается диагональной. обычное евклидово расстояние 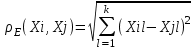 «взвешенное» евклидово расстояние 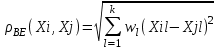 хеммингово расстояние 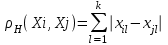 Принципы измерения расстояния между кластерами: «ближайшего соседа»: 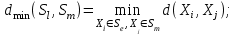 «дальнего соседа»: 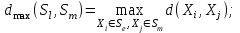 по «центрам тяжести» групп: 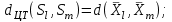 «средней связи»: 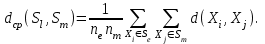 Наилучшее разбиение S* представляет собой такое разбиение, при котором достигается экстремум выбранного функционала качества. Выбор функционала качества основывается на эмпирических соображениях. Рассмотрим некоторые наиболее распространенные функционалы качества разбиения. Пусть исследованием выбрана метрика 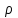 в пространстве Х и S=(S1,S2..Sp) некоторое фиксированное разбиение наблюдений x1,x2,…xn на заданное число p классов S1,S2..Sp. в пространстве Х и S=(S1,S2..Sp) некоторое фиксированное разбиение наблюдений x1,x2,…xn на заданное число p классов S1,S2..Sp. Существуют следующие характеристики функционала качества: суммавнутриклассовыхдисперсий 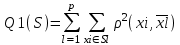 сумма попарных внутриклассовых расстояний между элементами 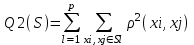 обобщеннаявнутриклассоваядисперсия 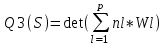 , ,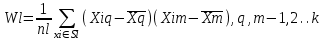 Иерархические процедуры являются наиболее распространенными алгоритмами кластерного анализа по их реализации на ЭВМ. Они бывают двух типов: агломеративные и дивизимные. В агломеративных процедурах начальным является разбиение, состоящее из n одноэлементных классов, а конечным – из одного класса; в дивизимных наоборот. k-means (иногда называемый k-средних) - наиболее популярный метод кластеризации. Был изобретён в 1950-х математиком Г. Штейнгаузом и почти одновременно С. Ллойдом. Особую популярность приобрёл после работы МакКвина. Действие алгоритма таково, что он стремится минимизировать суммарное квадратичное уклонение точек кластеров от центров этих кластеров: 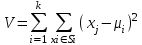 , где k - - число кластеров, Si - полученные кластеры, i=1,2,…,k и µi- центры масс векторов xj , где k - - число кластеров, Si - полученные кластеры, i=1,2,…,k и µi- центры масс векторов xj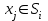 . .Для классификации используются различные методы. Основныеизних: классификация с помощью деревьев решений; байесовская (наивная) классификация ; классификация при помощи искусственных нейронных сетей; классификацияметодомопорныхвекторов; статистические методы, в частности, линейная регрессия; классификация при помощи метода ближайшего соседа; классификация CBR-методом; классификация при помощи генетических алгоритмов. |
