Алгебраические системы замыканий. Алгебраические системы замыканий - StudentLib.com. Библиографический список 23

• Название: Библиографический список 23
• Анкор: Алгебраические системы замыканий
• Дата: 26.09.2021
• Размер: 0.75 Mb.
• Имя файла: Алгебраические системы замыканий - StudentLib.com.doc
• Тип: Реферат; #236981
• страница: 4 из 6

§3. Алгебраические системы замыканий

Начнем с понятия алгебраической операции.

Пусть A – универсальная алгебра с множеством алгебраических операций Ω. Каждая операция ω из Ω имеет определённую арность n, n N {0}.

Для любого натурального n n-арная операция ω – это отображение из Aⁿ в A, то есть каждой упорядоченной n-ке {a₁; …; a_n} Aⁿ операция ω ставит в соответствие однозначно определённый элемент ω(a₁; …; a_n) из A.

В случае п = 1 это будет любое преобразование множества A (отображение A в себя).

Если n = 0, то a⁰ – это одноэлементное множество и 0-арная операция ω переводит элемент a⁰ в некоторый элемент ω(a⁰) = ω из A, то есть 0-арная операция ω фиксирует некоторый элемент в A: является некоторым выделенным элементом алгебры A.

Если дана универсальная алгебра A с множеством алгебраических операций Ω, то подмножество B A называется подалгеброй алгебры A, если оно замкнуто относительно всех операций из Ω. Иными словами, для любого ω Ω, n 1, и любых а₁, а₂, …, а_п B должно быть

ω(а₁, а₂, …, а_п) B.

С другой стороны, элементы, отмечаемые в A всеми 0-арными операциями из Ω (если такие существуют), должны содержаться в подалгебре B.

Очевидно, что пересечение любой системы подалгебр универсальной алгебры A, если оно не пусто, будет подалгеброй этой алгебры.

Отсюда следует, что если X – непустое подмножество алгебры A, то в A существует наименьшая среди подалгебр, содержащих целиком множество X. То есть существует наименьшая подалгебра в A, содержащая X и она равна пересечению всех подалгебр алгебры A, содержащих X. Обозначим её через и назовём подалгеброй, порожденной множеством X.

Стоит отметить, что пересечение подалгебр может быть пустым, если множество алгебраических операций Ω алгебры не содержит 0-арных операций.

Заметим, что система S(А) всех подалгебр алгебры A является алгебраической системой замыканий, то есть соответствующий оператор замыкания X является алгебраическим.

Очевидно, что соответствие X является оператором замыкания. Проверим, является ли он алгебраическим.

Возьмём a , тогда a будет принадлежать и , где – конечное подмножество множества X, так как элемент a получается путём применения конечного числа конечноместных n-арных операций ω Ω.

Справедливо и обратное утверждение:

Если D – произвольная алгебраическая система замыканий на множестве A, то для подходящего набора алгебраических операций Ω и соответствующей структуры универсальной алгебры на A, имеем S(A) = D.

Для доказательства обозначим через (X) оператор замыкания для алгебраической системы замыканий D на множестве A. Зададим алгебраические операции на A следующим образом. Каждой n-ке a₁, …, a_n 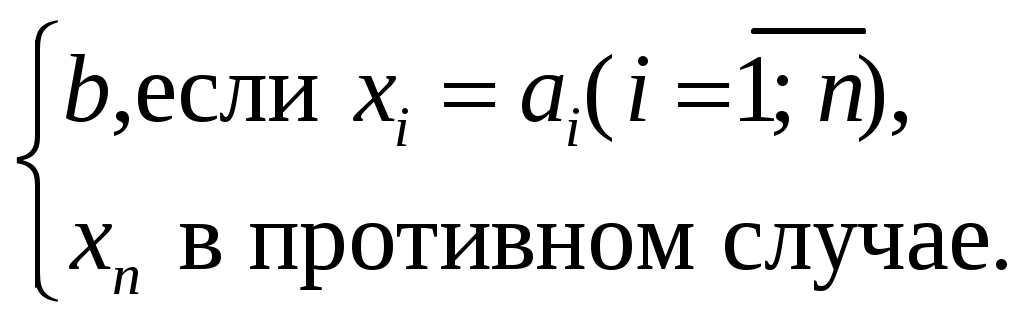A, где n N, и произвольному элементу b ({a₁, …, a_n}) поставим в соответствие свою n-арную операцию ω, определенную следующим правилом:

ω(x₁, …, x_n) = (4)

Это определяет структуру универсальной алгебры на A, где для каждого натурального числа n операции из Ω заданы формулой (4). Таким образом определено бесконечно много алгебраических операций на множестве A, если A бесконечно.

Пусть _Ω(X) =  – оператор замыкания, соответствующий системе S(A) подалгебр универсальной алгебры A. Проверим, что (X) = _Ω(X).

Пусть X A и предположим сначала, что X конечно, то есть X = {c₁, …, c_m}. Тогда (X) _Ω(X) по определению (4) алгебраических операций ω.

C другой стороны, так как (X) = (X), то для любой n-ки a₁, …, a_n (X) и для любой n-арной операции ω Ω ω(a₁, …, a_n) ({a₁, …, a_n}) (X) = (X). Поэтому (X) является подалгеброй алгебры и, значит, _Ω(X) (X).

Пусть теперь X – произвольное подмножество множества A, тогда, так как оба оператора замыкания (X) и _Ω(X) – алгебраические (первый по предположению, а второй в силу доказанного выше), имеем

(X) = (X ') = _Ω(X ') = _Ω(X),

где X ' пробегает конечные подмножества множества X.

Итак, доказан следующий результат:

Теорема 2. Система S(A) подалгебр универсальной алгебры A является алгебраической системой замыканий. Обратно, если дана алгебраическая система замыканий D на множестве A, то для подходящего множества алгебраических операций Ω можно определить такую структуру универсальной алгебры на A, что S(A) = D.

Полученный выше результат можно использовать при построении оператора замыкания_Ω(X), соответствующего системе S(A) подалгебр универсальной алгебры A.

Отметим, что примеры 1 и 3 дают алгебраические системы замыканий, а система замкнутых множеств топологического пространства (пример 2), как правило, не алгебраическая.