§ 5. Задачи
Задача 1. Установить, что при соответствии Галуа X X*, Y X*, Y Y* выполняется тождество ( Y* выполняется тождество ( Xi)* = Xi)* = 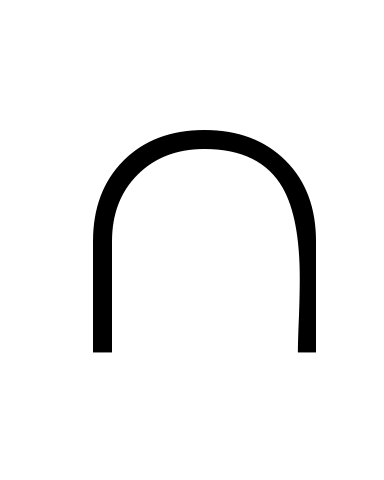 Xi*, для произвольных семейств подмножеств (Xi)i Xi*, для произвольных семейств подмножеств (Xi)i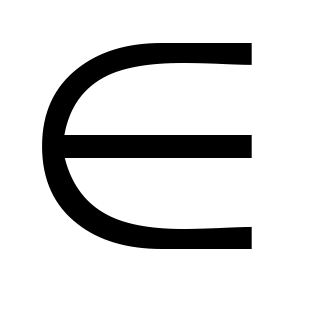 I. I.
Решение:
Без ограничения общности возьмём два множества X1 и X2 и покажем, что (X1 X2)* = X1* X2)* = X1*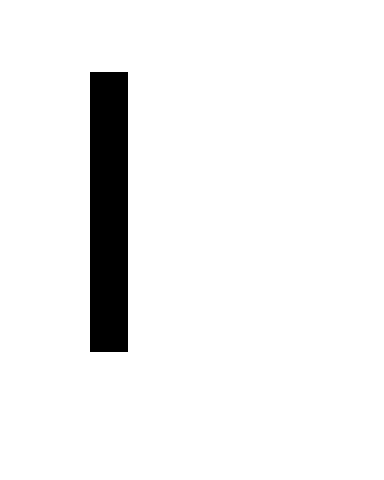 X2*. X2*.
Множеству X1 поставим в соответствие множество X1*:
X1* = {y1 B|(x1, y1) B|(x1, y1) Ф для всех x1 Ф для всех x1 X1}. X1}.
Аналогично для множества X2:
X2* = {y2 B|(x2, y2) B|(x2, y2) Ф для всех x2 Ф для всех x2 X2}. X2}.
Пусть X3 =X1 X2. Тогда (X1 X2. Тогда (X1 X2)* или X3* будет иметь следующую структуру: X3* = {y3 X2)* или X3* будет иметь следующую структуру: X3* = {y3 B|(x3, y3) B|(x3, y3) Ф для всех x3 Ф для всех x3 X3} или другими словами это такие y3 из B, что пары (x1, y3) и (x2, y3) должны принадлежать соответствию Ф одновременно для всех x1 и x2 из X1 X3} или другими словами это такие y3 из B, что пары (x1, y3) и (x2, y3) должны принадлежать соответствию Ф одновременно для всех x1 и x2 из X1 X2. То есть множество элементов y3 из B это множество, состоящее из элементов y1 X2. То есть множество элементов y3 из B это множество, состоящее из элементов y1 X1* и y2 X1* и y2 X2*, которые одновременно должны удовлетворять соотношениям (x1, y1) X2*, которые одновременно должны удовлетворять соотношениям (x1, y1) Ф, (x1, y2) Ф, (x1, y2) Ф, (x2, y1) Ф, (x2, y1) Ф, (x2, y2) Ф, (x2, y2) Ф. То есть элементы y3 принадлежат пересечению множеств X1* и X2*, что и требовалось показать. Ф. То есть элементы y3 принадлежат пересечению множеств X1* и X2*, что и требовалось показать.
Задача 2. Пусть X H(X) – произвольное отображение множества B (A) в себя. Показать, что (X) = H(X) H(X) – произвольное отображение множества B (A) в себя. Показать, что (X) = H(X) X определяет оператор замыкания тогда и только тогда, когда X X определяет оператор замыкания тогда и только тогда, когда X (Y) влечёт (X) (Y) влечёт (X) (Y). (Y).
Решение:
докажем прямое утверждение: если (X) = H(X) X определяет оператор замыкания тогда X X определяет оператор замыкания тогда X (Y) влечёт (X) (Y) влечёт (X) (Y). (Y).
Пусть X (Y), то есть X (Y), то есть X H(Y) H(Y) Y. Так как по условию (Y) = H(Y) Y. Так как по условию (Y) = H(Y) Y – оператор замыкания, то для него выполняются аксиомы J. 1 – J. 3. Применим аксиому J. 1 к X Y – оператор замыкания, то для него выполняются аксиомы J. 1 – J. 3. Применим аксиому J. 1 к X H(Y) H(Y) Y и аксиому J. 3 к ((Y)): Y и аксиому J. 3 к ((Y)):
X H(Y) H(Y) Y Y 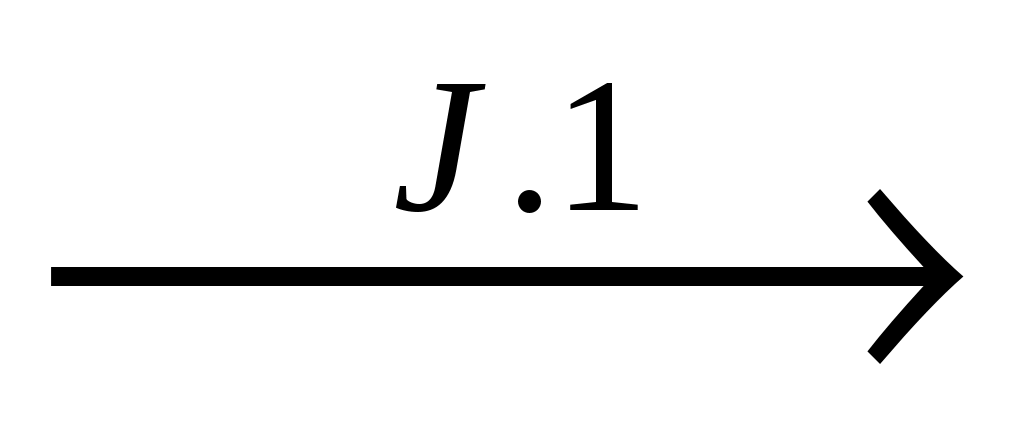 H(X) H(X) X X H(H(Y) H(H(Y) Y) Y) (H(Y) (H(Y) Y) Y) H(X) H(X) X X H(Y) H(Y) Y. То есть (X) Y. То есть (X) (Y). (Y).
докажем обратное утверждение: если X (Y) влечёт (X) (Y) влечёт (X) (Y) тогда (X) = H(X) (Y) тогда (X) = H(X) X определяет оператор замыкания. X определяет оператор замыкания.
Для доказательства обратного утверждения, необходимо проверить выполнимость аксиом J. 1 – J. 3 оператора замыкания.
Для начала докажем вспомогательное утверждение о том, что Y X* тогда и только тогда, когда X X* тогда и только тогда, когда X Y*. Y*.
Доказательство:
∆ Докажем прямое утверждение.
Пусть Y X*. Тогда, применив к нему свойство (7), получим Y* X*. Тогда, применив к нему свойство (7), получим Y*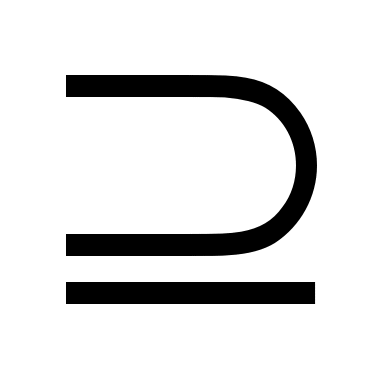 X**. По свойству (7) имеем включение X X**. По свойству (7) имеем включение X X**. Следовательно, получаем X X**. Следовательно, получаем X X** X** Y* или X Y* или X Y*. Y*.
Докажем обратное утверждение.
Пусть X Y*. Тогда X* Y*. Тогда X*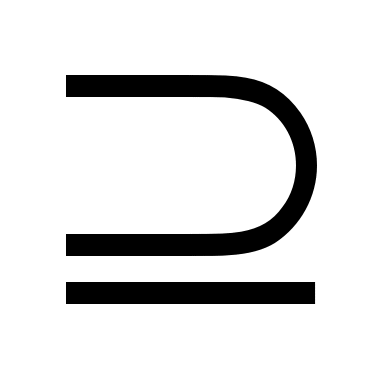 Y** Y**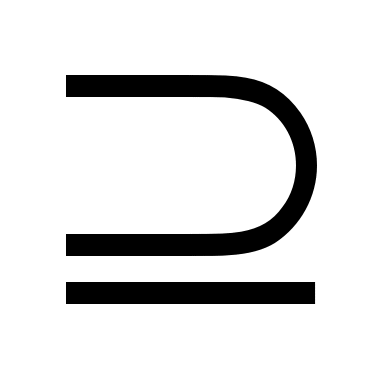 Y ▲ Y ▲
J. 1: пусть X Y и Y Y и Y (X), тогда по доказанному выше утверждению включение Y (X), тогда по доказанному выше утверждению включение Y (X) равносильным образом можно заменить на X (X) равносильным образом можно заменить на X (Y). Получим, что X (Y). Получим, что X X X (Y) или X (Y) или X (Y). Тогда по условию пункта b) задачи X (Y). Тогда по условию пункта b) задачи X (Y) влечёт (X) (Y) влечёт (X) (Y). Следовательно, если X (Y). Следовательно, если X Y, то (X) Y, то (X) (Y). (Y).
J. 2: пусть X Y и Y Y и Y (X) по утверждению, значит, X (X) по утверждению, значит, X (X). (X).
J. 3: по J. 2 X (X). Применим к нему свойство (7), получим (X) (X). Применим к нему свойство (7), получим (X)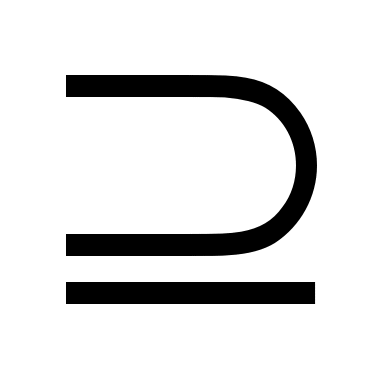 (X). Применим это же свойство к X (X). Применим это же свойство к X (Y) (Y) (X) (X) (Y), получим (X) (Y), получим (X)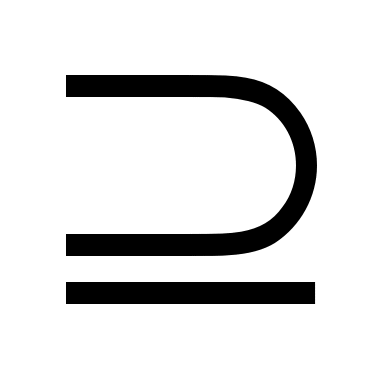 (Y) (Y) (X) (X)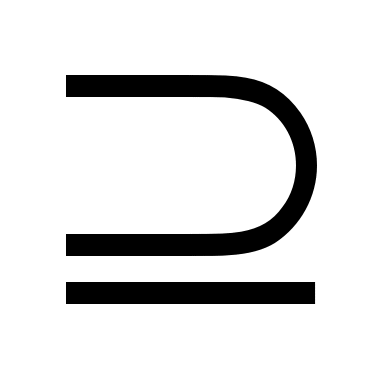 (Y). Далее по утверждению Y (Y). Далее по утверждению Y (X) (X) (Y) (Y)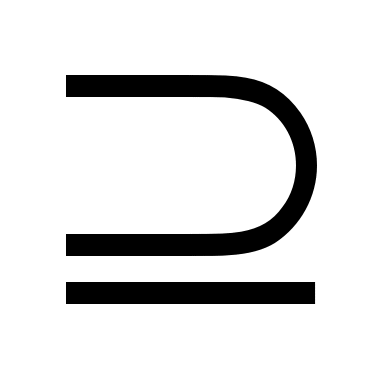 (X). Получили (Y) (X). Получили (Y)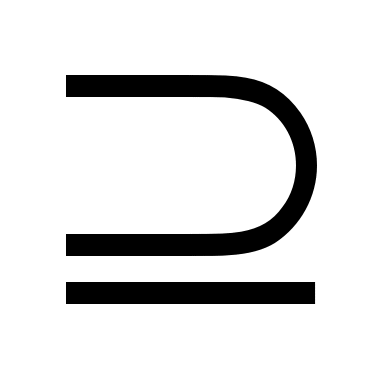 (X) (X)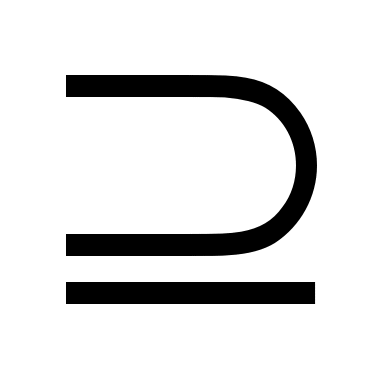 (Y). При этом (Y) (Y). При этом (Y)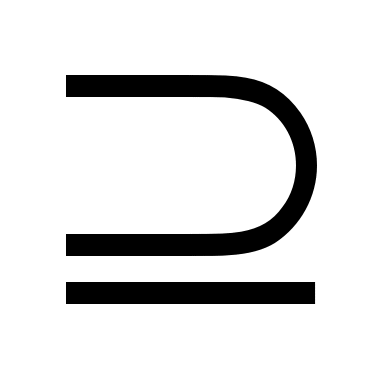 (X) (по утверждению). Следовательно, мы получаем обратное включение (X) (X) (по утверждению). Следовательно, мы получаем обратное включение (X) (X). Тем самым получили, что (X) = (X). (X). Тем самым получили, что (X) = (X).
Следовательно, (X) = H(X) X – оператор замыкания. X – оператор замыкания.
Задача 3. Показать, что множество всех предупорядоченностей ρ на множестве A является алгебраической системой замыканий. Верно ли это для множества всех упорядоченностей?
Решение:
Непустое множество 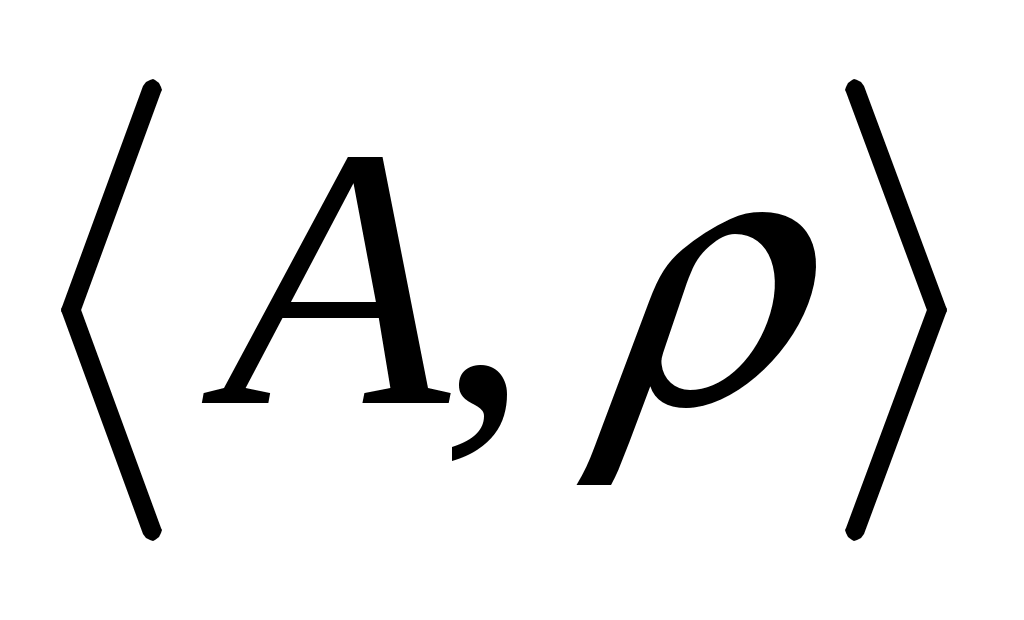 назовём предупорядоченным, если введенное на нём бинарное отношение ρ рефлексивно и транзитивно. Такое отношение ρ называется отношением предпорядка на A. назовём предупорядоченным, если введенное на нём бинарное отношение ρ рефлексивно и транзитивно. Такое отношение ρ называется отношением предпорядка на A.
Пусть X A A A, или X A, или X B (A B (A A). Обозначим через J(X) пересечение всех предпорядков на A, содержащих X: A). Обозначим через J(X) пересечение всех предпорядков на A, содержащих X:
J(X) = 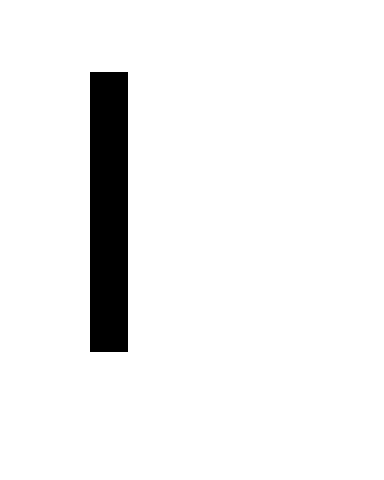 {ρ – предпорядок на A: X {ρ – предпорядок на A: X ρ}. ρ}.
Так как при пересечении бинарных отношений на множестве свойства рефлексивности и транзитивности сохраняются, то J(X) – наименьший предпорядок на A, содержащий X. Ясно, что A A является предпорядком на A. Поэтому система всех предпорядков на A является системой замыканий на этом множестве. A является предпорядком на A. Поэтому система всех предпорядков на A является системой замыканий на этом множестве.
Остаётся проверить, будет ли система предпорядков алгебраической. Для этого возьмём произвольную пару (a, b) J(X), где X J(X), где X A A A. Предпорядок J(X) получается из множества пар X добавлением пар вида (c, c), где c A. Предпорядок J(X) получается из множества пар X добавлением пар вида (c, c), где c A, и его расширением по транзитивности: если уже получены пары (d, e) и (e, f), то добавляем и пару (d, f). При этом пара (a, b) в результате последовательного применения расширений по рефлексивности и транзитивности принадлежит конечному множеству пар F A, и его расширением по транзитивности: если уже получены пары (d, e) и (e, f), то добавляем и пару (d, f). При этом пара (a, b) в результате последовательного применения расширений по рефлексивности и транзитивности принадлежит конечному множеству пар F X. Следовательно, (a, b) X. Следовательно, (a, b) J(F). J(F).
Для множества всех упорядоченностей верно лишь в том случае, когда множество A содержит один элемент. Иначе, не выполняется свойство антисимметричности.
Задача 4. Показать, что совокупность всех алгебраических систем замыканий на данном множестве A является системой замыканий на B (A). Всегда ли эта система замыканий будет алгебраической?
Решение:
Очевидно, что множество всех алгебраических систем замыкания на данном множестве A является системой замыкания на булеане B (A). Чтобы показать, является ли эта система алгебраической, воспользуемся теоремой 2.
Будем считать, что имеется семейство алгебр 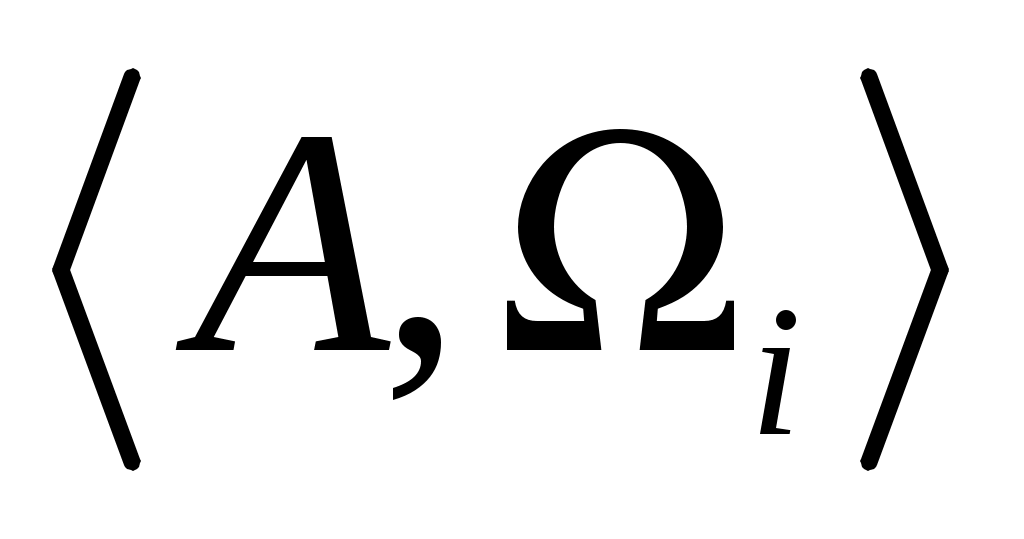 , i , i I. Каждой из них поставлена система подалгебр S( I. Каждой из них поставлена система подалгебр S(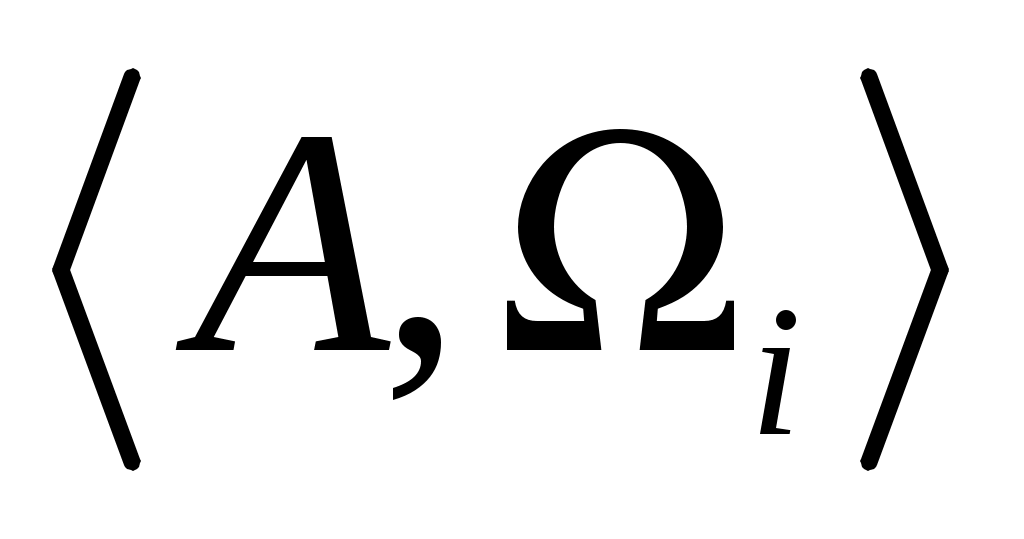 ). Пересечению соответствующих систем замыканий соответствует алгебра ). Пересечению соответствующих систем замыканий соответствует алгебра 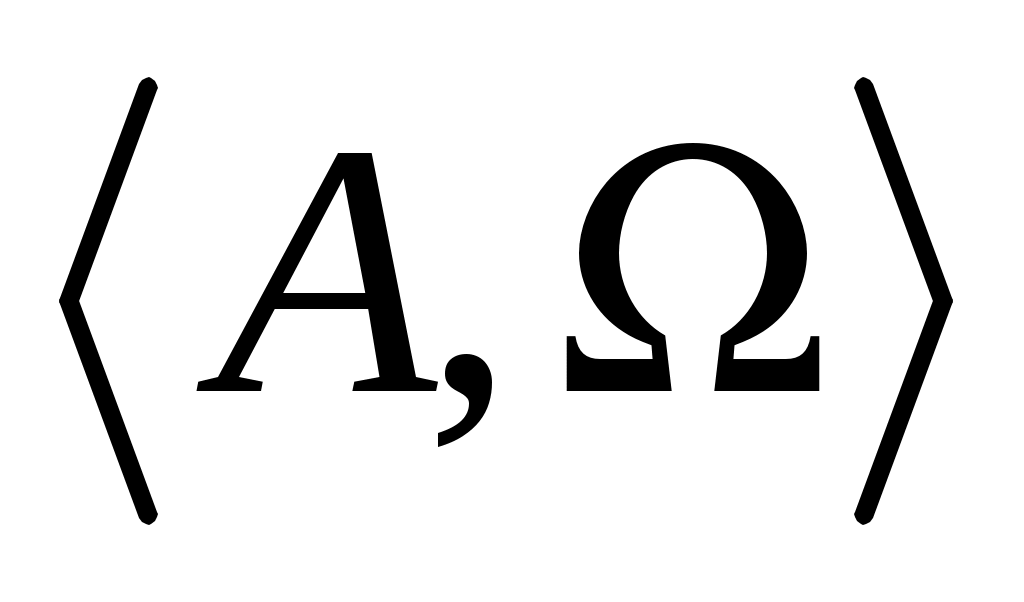 , при Ω= , при Ω=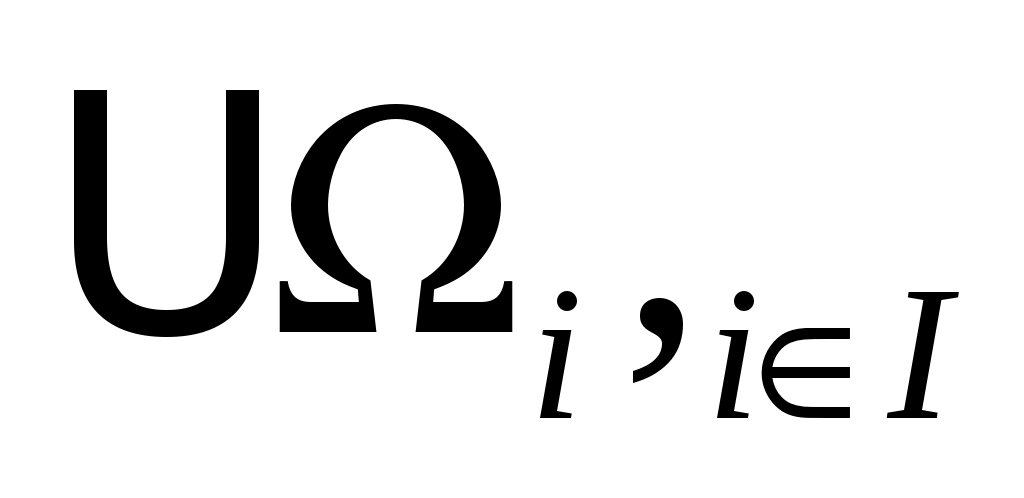 . Для произвольного подмножества X в A рассмотрим подалгебру . Для произвольного подмножества X в A рассмотрим подалгебру 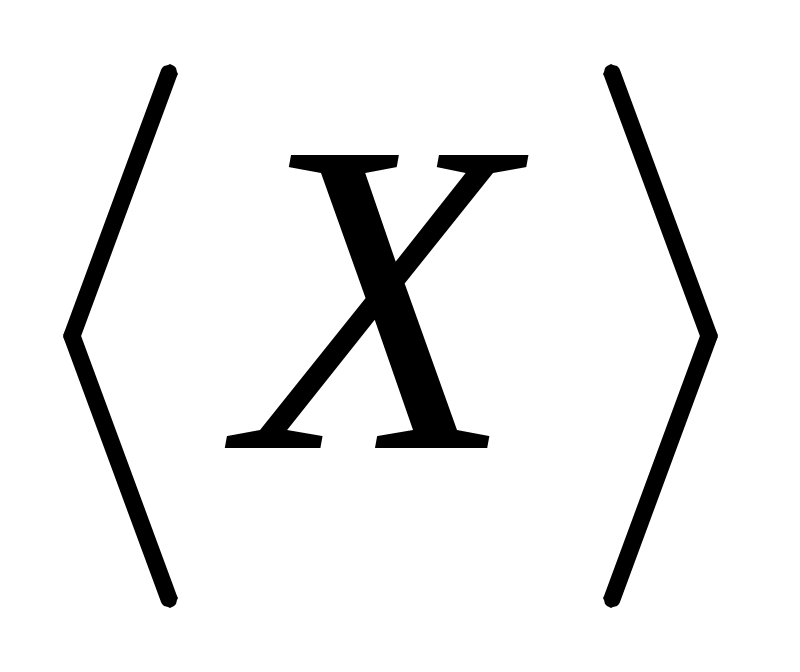 алгебры алгебры 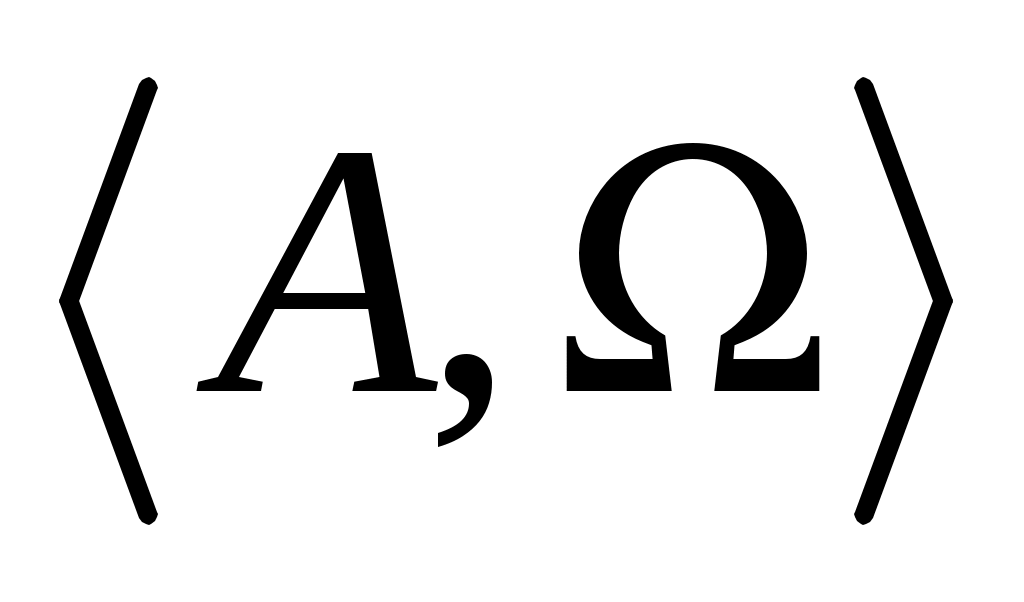 . И возьмём элемент a из . И возьмём элемент a из 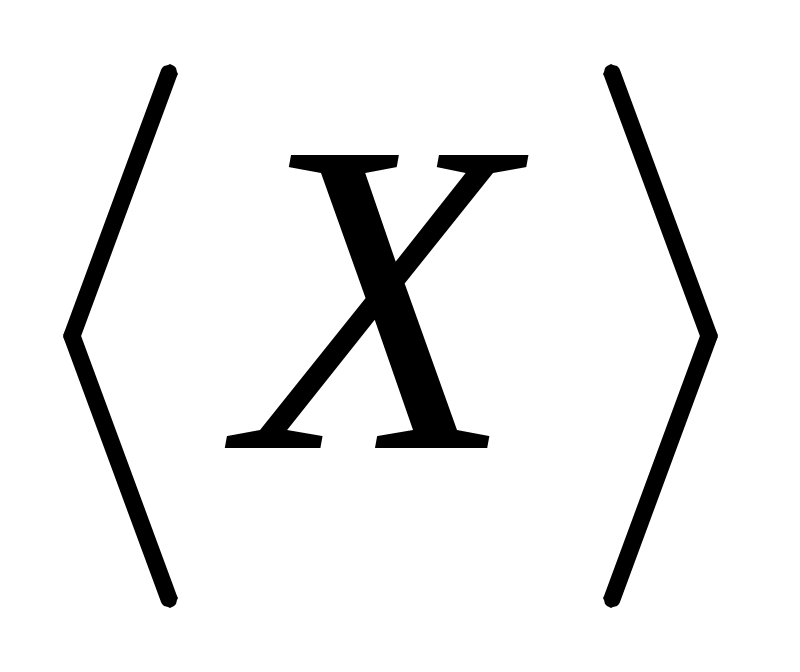 . Элемент a выражается через конечное множество . Элемент a выражается через конечное множество 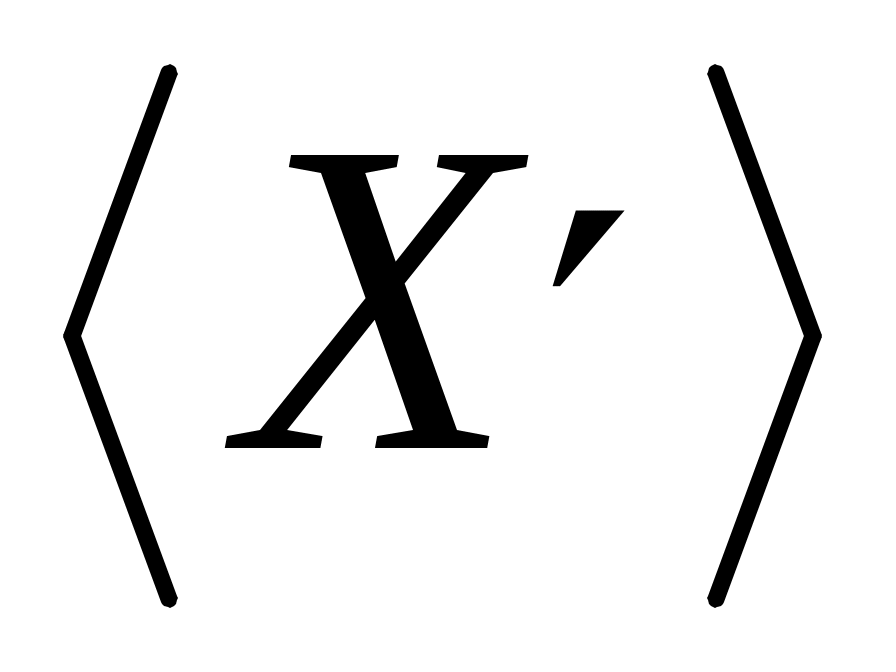 элементов из элементов из 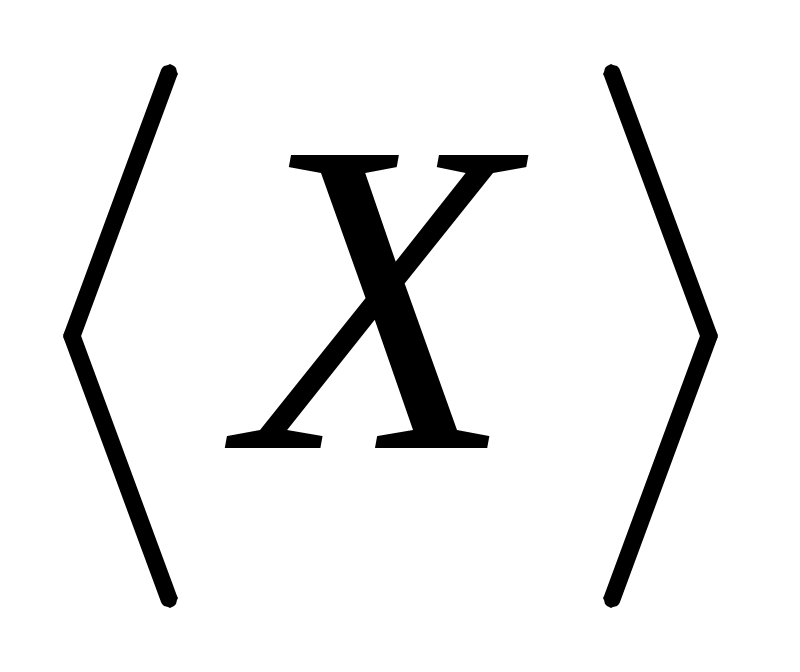 с помощью последовательного применения конечного числа операций из Ω. Следовательно, a принадлежит замыканию с помощью последовательного применения конечного числа операций из Ω. Следовательно, a принадлежит замыканию 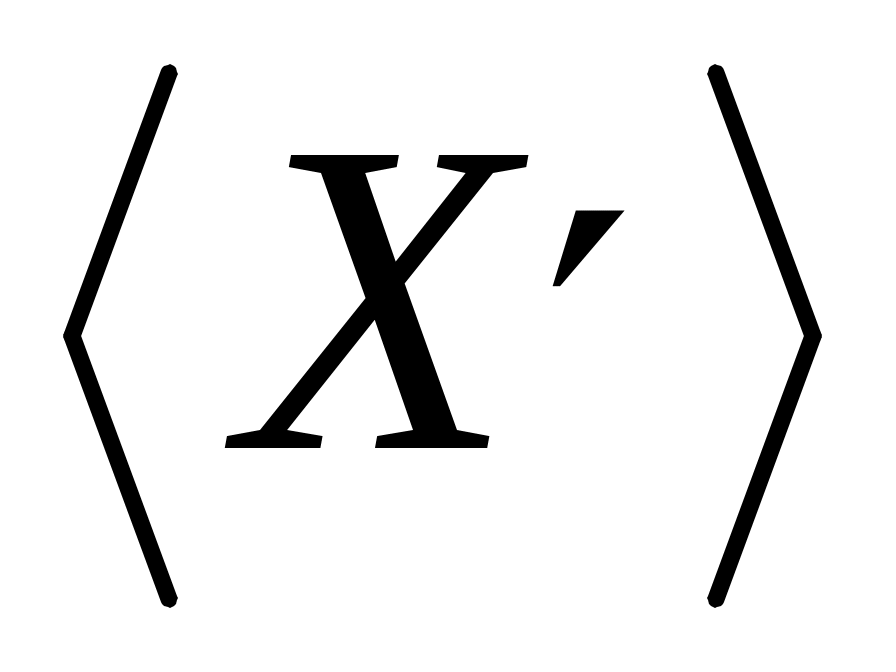 . .
Библиографический список
Кон П. Универсальная алгебра – М.: Мир, 1968. – 352 с.
Курош А. Г. Лекции по общей алгебре – М.: Наука, 1973. – 400 с.
Курош А. Г. Курс высшей алгебры – СПб.: Лань, 2006. – 432 с.
Оре О. Теория графов – М.: Наука, 1968. – 336 с.
Общая алгебра. Т. 1 / под общ. ред. Л. А. Скорнякова – М.: Наука, 1990. – 592 с.
Постников М. М. Теория Галуа – М.: Издательство физико-математической литературы, 1963. – 220 с.
Риге Ж., Бинарные отношения, замыкания, соответствия Галуа // Кибернетический сборник / под ред. А. А. Ляпунова, О. Б. Лупанова. – вып. 7. – М.: Издательство иностранной литературы, 1963. – С. 129-185.
|
 Скачать 0.75 Mb.
Скачать 0.75 Mb.