Курсовая работа. Биномиальные коэффициенты
 Скачать 0.86 Mb.
|
|
ТАБЛИЦА 2 Продолженный вверх треугольник Паскаля.
Если r не является неотрицательным целым, то биномиальная теорема чаще всего используется в частном случае у = 1. Сформулируем этот частный случай явно, заменив х на z, чтобы подчеркнуть тот факт, что здесь может присутствовать произвольное комплексное число:   <1 (2.13)Если подставить сюда z = х/у и умножить обе части на y  , то из этой формулы вытекает общая формула (2.12). Мы доказали, исходя из комбинаторной интерпретации, биномиальную теорему только для целого неотрицательного r. Мы лишены возможности вывести формулу для общего случая из случая целого неотрицательного г, используя полиномиальную аргументацию, ибо в общем случае сумма бесконечна. Однако в случае произвольного r можно воспользоваться теоремой Тейлора из анализа:  Производные функции f (z) = (1+z) легко вычисляются: в самом деле, . А подстановка z = 0 дает (2.13).Кроме того, нужно доказать, что бесконечная сумма сходится при < 1. И это действительно так, поскольку согласно равенству  O  которое приводится ниже. А теперь займемся вплотную величинами  при целом отрицательном n. Один из способов подступиться к этим величинам состоит в том, чтобы использовать правило сложения (2.8) для заполнения табл.1 элементами, которые лежат выше имеющихся чисел, получая тем самым табл.2 . Все эти числа нам уже знакомы. Действительно, ряды и колонки из табл.2 оказываются колонками из табл. 1 (за вычетом знака „минус"). Так что между величинами при отрицательных и положительных п должна существовать некая связь. Общее правило таково:  ,целое k, (2.14)что легко доказать, поскольку   при k ≥ 0, а при k < 0 обе части равны нулю. Особенно ценно то, что соотношение (2.14) выполняется без всяких ограничений. (Разумеется, нижний индекс должен быть целым с тем, чтобы были определены биномиальные коэффициенты.) Преобразование (2.14) называется обращением верхнего индекса, или просто „верхним обращением" Если все соотношения, с которыми мы уже имели дело,—соотношения симметрии, внесения, сложения и т. п.—были довольно бесхитростны, то это соотношение выглядит весьма замысловато. Тем не менее, существует мнемоническое правило, что само по себе не так уж и плохо. Обращение верхнего индекса начинается с записи (-1)  , где k - нижний индекс. (Нижний индекс не должен изменяться.) Затем мы сразу же снова записываем k дважды: на места верхнего и нижнего индексов. Потом обращается исходный верхний индекс путем его вычитания из нового верхнего индекса. И в завершение вычитается еще 1 (всегда вычитая, а не прибавляя, ибо это процесс обращения). Для закрепления материала два раза подряд обратим верхний индекс. Имеем  ,и мы вернулись к тому, с чего начали. Вряд ли это то, к чему мы стремились, воссоздав данное соотношение,—но приятно сознавать, что мы не сбились с пути. Разумеется, имеются более полезные применения соотношения (2.14) чем это. Так, верхнее обращение можно использовать для перемещения величин из верхнего на место нижнего индекса и наоборот. Соответствующее соотношение имеет симметричную форму:  , целые m,n ≥ 0, (2.15)Кроме того, верхнее обращение может быть использовано для вывода следующей интересной формулы суммирования:  целоеm. (2.16) Идея вывода этой формулы состоит в том, чтобы сперва обратить верхний индекс, затем применить формулу (2.9), а потом снова обратить индекс:  Эта формула дает частичную сумму r-го ряда треугольника Паскаля, при условии что элементам данного ряда приписаны чередующиеся знаки. Так, при r= 5 и m = 2 эта формула дает 1-5+10=6=(-1)  Обратите внимание, что при m ≥ r формула (2.16) дает знакочередующуюся сумму элементов всего ряда, а такая сумма равна нулю при целом положительном г. Это уже было доказано при разложении (1- 1) в соответствии с биномиальной теоремой — интересно то, что частичные суммы такого разложения могут быть вычислены в замкнутой форме. А как насчет более простой частичной суммы  (2.17)Если мы умеем вычислять соответствующую знакочередующуюся сумму, то наверняка должны суметь вычислить и эту. А вот и нет: для частичной суммы элементов ряда треугольника Паскаля не существует замкнутого выражения. Мы умеем вычислять суммы элементов в колонках —это формула (2.10),—но не в рядах. Можно вычислить частичные суммы элементов ряда, если умножить их на расстояние от центра:  целое m. (2.18)(Эта формула легко проверяется индукцией по m.) Взаимосвязь между этими частичными суммами — имеющими и не имеющими множитель (r/2 —k) в общем члене — аналогична взаимосвязи между интегралами  и  .Явно более сложный интеграл слева с множителем х выражается в замкнутой форме, в то время как более простой на вид интеграл справа без такого множителя —не выражается. Внешность бывает обманчивой. В конце этой главы мы разберем метод, с помощью которого можно определить, выражаются или нет в замкнутой форме частичные суммы некоторого заданного ряда с биномиальными коэффициентами - в достаточно общей постановке. Данный метод в состоянии обнаружить формулы (2.16) и (2.18), а. также позволяет выяснить, что нахождение формулы для (2.17) - гиблое дело. Частичные суммы биномиального ряда приводят к другого рода соотношению:  целое m (2.19)Не составляет труда доказать это соотношение по индукции: при m < 0 обе части равны нулю, а при m = 0 равны 1. Если обозначить сумму в левой части через S  , то, воспользовавшись формулой сложения (2.8), легко показать, что  ,и   при m > 0. Следовательно,  а правая часть (2.19) также удовлетворяет этому рекуррентному соотношению. По индукции, обе части должны быть равны — чтд. Но есть более тонкое доказательство. Если r—целое число из промежутка 0 ≥ г ≥ -m, то биномиальная теорема показывает, что обе части (2.19) равны  . А поскольку обе части представляют собой многочлены относительно г степени та или меньшей, то совпадения их только в m + 1 различных точках достаточно для установления равенства в общем случае. Вроде бы глупо обзаводиться соотношением, где одна сумма равна другой. Тем более, что ни одна из них не выражается в замкнутой форме. Но иногда вычислить одну сумму оказывается проще, чем другую. К примеру, если положить х = - 1 и у = 1, то получим альтернативную форму соотношения (2.16):  ,целое m≥0.А если положить x=y=1 и r=m+1, то получим  .В левой части просуммирована только половина биномиальных коэффициентов с верхним индексом 2m +1, а эти коэффициенты равны своим двойникам в правой половине, поскольку треугольник Паскаля обладает лево-правосторонней симметрией. Следовательно, левая часть —это просто  , и мы получаем формулу, которую никак не ожидали получить:  целое m ≥0. (2.20)Проверим ее при m = 2:  До сих пор мы рассматривали либо отдельные биномиальные коэффициенты, либо суммы, в члены которых входило только по одному биномиальному коэффициенту. Но многие из бросающих нам вызов задач включают в себя произведения двух и более биномиальных коэффициентов, поэтому оставшуюся часть этого раздела мы посвятим рассмотрению именно таких случаев. Вот удобное правило, которое зачастую помогает упростить произведение двух биномиальных коэффициентов:  ,целые m, k. (2.21)Мы уже встречались с частным случаем k = 1 — правилом внесения (2.6). Хотя как одна, так и другая части (2.21) суть произведения биномиальных коэффициентов, зачастую одну из них просуммировать проще, чем другую, благодаря взаимодействию с другими частями формулы. Так, та встречается в левой части дважды, а в правой — лишь однажды. Поэтому при суммировании по m мы, естественно, предпочитаем заменить  .Равенство (2.21) справедливо исключительно по причине взаимного сокращения m! в факториальных представлениях  и  . Если все переменные - целые числа r≥m≥k≥, то  Здесь не было ничего сложного. К тому же, если m < k или k < 0, то обе части (2.21) равны нулю, так что данное соотношение выполняется при любых целых m и k. Наконец, посредством полиномиальной аргументации его можно распространить на все вещественные r. Биномиальный коэффициент вида 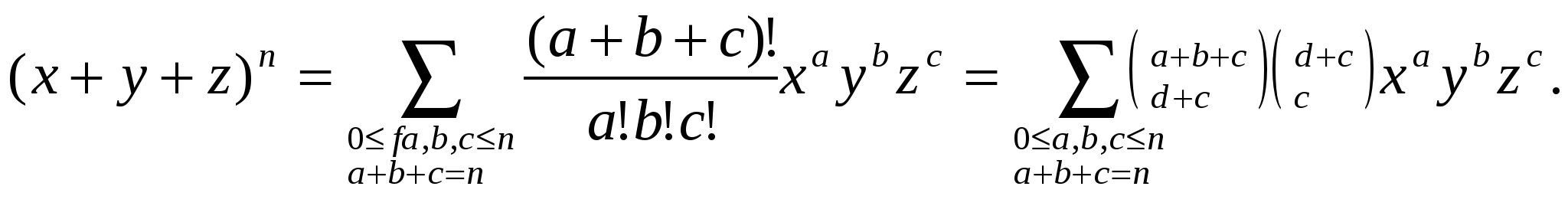 можно переписать в виде (a+b)!/a! b! после соответствующего переобозначения переменных. Аналогично, величину r!/k! (m - k)! (r - m)! в середине предыдущей выкладки можно переписать в виде (а + b + с)!/а! b! с!. Это „триномиальный коэффициент" который возникает в „триномиальной теореме":  Таким образом,  — это на самом деле триномиальный коэффициент в другом обличий. Время от времени триномиальные коэффициенты возникают в приложениях, и их обычно записывают как  чтобы подчеркнуть наличие симметрии. Обобщением биномиальных и триномиальных коэффициентов служат мультиномиальные коэффициенты, которые всегда выражаются в виде произведения биномиальных коэффициентов: 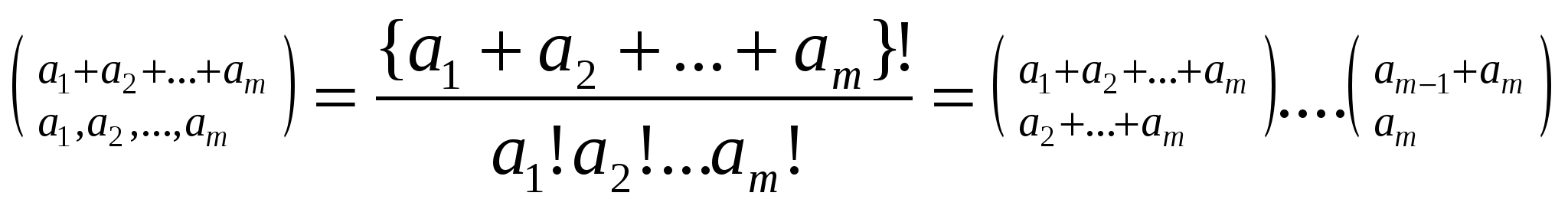 .ТАБЛИЦА 3. Суммы произведений биномиальных коэффициентов.  целые m,n. (2.22) целое l ≥ 0, целые m, n. (2.23) целое l ≥ 0, целые m, n. (2.24) целые l ,m,n ≥ 0. (2.25) целые l, m ≥ 0, целые n ≥ q ≥ 0. (2.26)Вот мы и добрались до табл.3, в которой перечислены наиболее важные из числа испытанных нами тождеств. Это те тождества, на которые мы опираемся в противоборстве с суммой, включающей в себя произведение двух биномиальных коэффициентов. Каждое из этих тождеств представляет собой сумму по k с одним k в каждом биномиальном коэффициенте; помимо этого, в нее входит по четыре почти не зависящих друг от друга параметра, обозначаемых через m, n, r и т.д.,— по одному на месте каждого индекса. В зависимости от того, входит или нет k в верхний или нижний индекс, а также от того, с каким знаком он входит, мы имеем дело с разными случаями. А в некоторых случаях имеется и дополнительный множитель (-1) , необходимый для того, чтобы сумма вычислялась в замкнутой форме. Таблица 3 слишком уж сложна для запоминания; она предназначена только для справок. Однако первое тождество из этой таблицы запоминается гораздо легче остальных и его не следует забывать. Оно устанавливает, что сумма (по всем целым k) произведения двух биномиальных коэффициентов, в которых верхние индексы постоянны порознь, а нижние индексы постоянны в сумме при любом k, равна биномиальному коэффициенту, полученному путем сложения как верхних, так и нижних индексов. Данное тождество известно как свертка Вандермонда, поскольку Александр Вандермонд написал по этому поводу в конце 18- го века важную статью; однако еще в 1303 г. оно было известно Чжу Ши-цзе из Китая. Все остальные тождества в табл. 3 можно получить из свертки Вандермонда, аккуратно выполняя преобразования обращения верхнего индекса, применяя правило симметрии и т. п.,- следовательно, свертка Вандермонда является „самым основным" из всех основных тождеств. Правило свертки Вандермонда можно доказать, исходя из замечательной комбинаторной интерпретации. Если заменить k на k-m, a n на n-m, то можно считать, что m = 0; следовательно, требуется доказать тождество  , целое n. (2.27)Пусть r и s — целые неотрицательные числа (общий случай получается посредством полиномиальной аргументации). В правой части  —это число способов выбрать n человек из r мужчин и s женщин. В левой части каждый член суммы — это число способов выбрать k человек из r мужчин и n—k человек из s женщин. А суммирование по всем k учитывает каждую возможность ровно по одному разу. Как правило, эти тождества применяются слева направо, так как упрощение идет именно в этом направлении. Но иногда оправданно движение в обратном направлении, даже если приходится временно идти на усложнение. При этом обычно образуется двойная сумма, в которой можно изменить порядок суммирования и потом упростить. Перед тем как двинуться дальше, посмотрим, как доказываются еще два тождества из табл. 3. Тождество (2.23) доказать легко: нужно всего лишь заменить первый биномиальный коэффициент на  , а потом применить свертку Вандермонда (2.22). Следующее тождество, (2.24), несколько сложнее. Путем последовательных преобразований его можно свести к свертке Вандермонда, но можно доказать его столь же просто, если прибегнуть к старому испытанному методу математической индукции. Зачастую индукция —это первое, к чему мы прибегаем, если в голову не приходит ничего другого, но здесь индукция по l подходит как нельзя лучше. Действительно, при l = 0 все члены суммы равны нулю, за исключением члена с k = -m; так что обе части данного равенства равны  - А теперь предположим, что данное тождество справедливо при всех значениях, меньших некоторого фиксированного l, где l > 0. Можно воспользоваться формулой сложения для замены  ; тогда ппервоначальная сумма распадается на две суммы, каждую из которых можно вычислить, исходя из предположения  А если еще раз применить формулу сложения, то это упрощается и получается правая часть (2.24). В этом выводе заслуживают внимания две вещи. Во-первых, мы вновь убеждаемся в огромном преимуществе суммирования по всем целым k, а не по k в определенных пределах, поскольку не нужно беспокоиться по поводу граничных условий. Во- вторых, формула сложения чудесно стыкуется с математической индукцией, поскольку она представляет рекуррентную зависимость для биномиальных коэффициентов. Биномиальный коэффициент, верхний индекс которого есть l, выражается в виде суммы двух коэффициентов, верхние индексы которых суть l-1, а это именно то, что требуется для предположения индукции. А что можно сказать о суммах с тремя и более биномиальными коэффициентами? Если индекс суммирования разбросан по всем коэффициентам, то шансы отыскать сумму в замкнутой форме невелики: известно лишь несколько сумм такого рода, которые выражаются в замкнутой форме, и нужная нам сумма вполне могла не соответствовать предъявленным требованиям. Одна из таких редкостей:  , целые m,n ≥ 0. (2.28)А вот другой, более симметричный экземпляр:  , целые a, b, c ≥ 0 (2.29)У него есть двойник с двумя коэффициентами:  , целые a,b ≥ 0, (2.30)который, между прочим, не фигурирует в табл. 3. Аналогичная сумма с четырьмя коэффициентами не выражается в замкнутой форме, зато выражается другая подобная ей сумма: 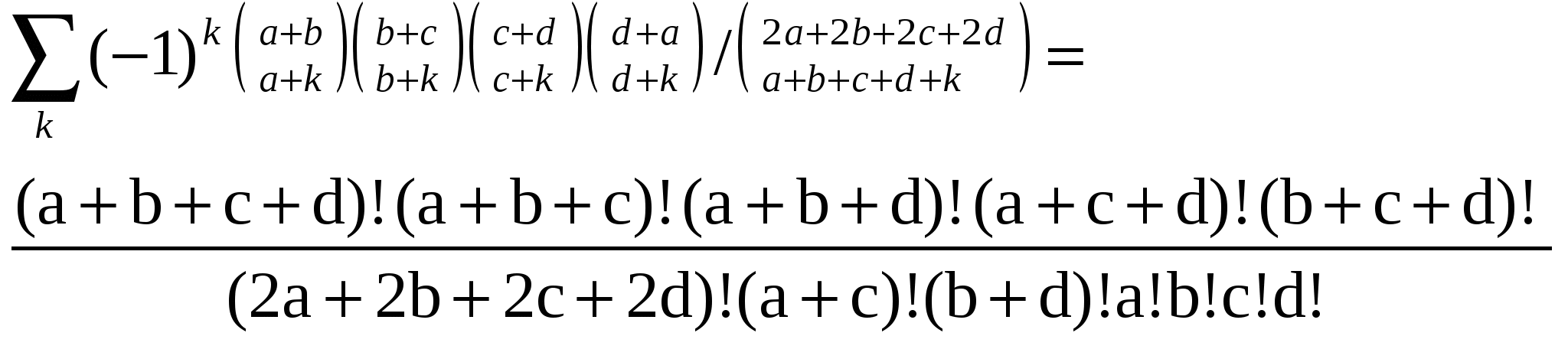 целые a,b,c,d ≥ 0. Это было обнаружено Джоном Дуголом в начале двадцатого столетия.  (2.31)целые а  ,а ,…,а ≥ 0 Это сумма по  переменным индексам k при 1 ≤ i < j < n. Равенство (2.29) —всего лишь ее частный случай при n = 3; в случае n = 4 ее можно переписать следующим образом, если воспользоваться обозначениями (a,b,c, d) вместо (a ,a2, а3, an) и (i, j,k) вместо ( ):  , целые а,b,c,d ≥ 0.Левая часть (2.31) —это коэффициент при 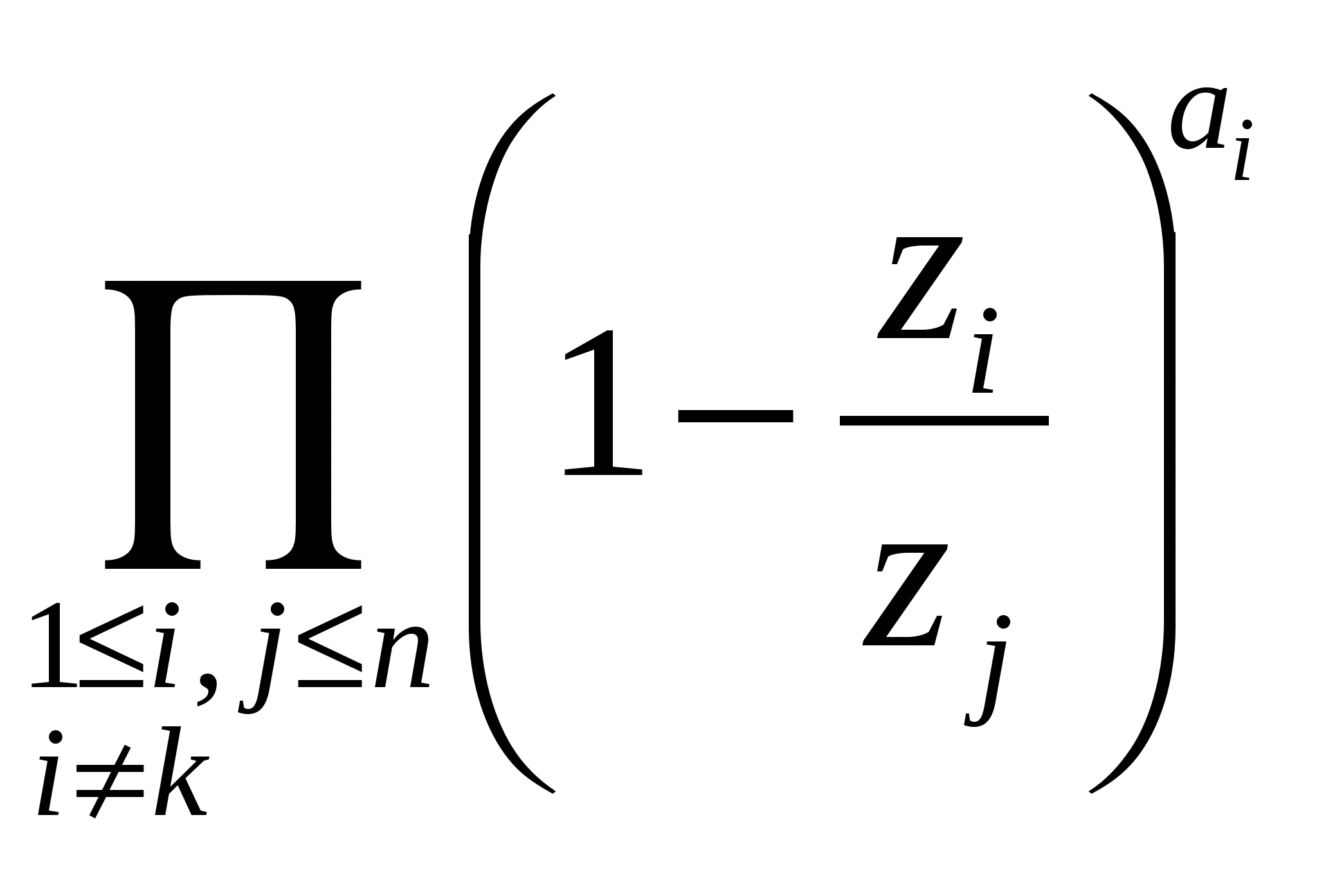 , получающийся после полного разложения произведения n(n — 1) дробей  по положительным и отрицательным степеням z. Предположение о виде правой части (2.З1) было высказано Фримэном Дайсоном в 1962 г. и вскоре после этого было доказано сразу несколькими людьми. Заслуживает внимания еще одно тождество, включающее в себя массу биномиальных коэффициентов:  , целые m,n,k ≥0 (2.32)Впрочем, мы уже отклоняемся от нашей темы „основные тождества" так что лучше остановиться и подвести итог пройденному материалу. Мы убедились, что биномиальные коэффициенты удовлетворяют такому разнообразию тождеств, которое способно сбить с толку. К счастью, некоторые из них легко запоминаются, и мы можем воспользоваться этим обстоятельством для выведения большинства других всего за несколько шагов. В табл. 4 сведены десять наиболее полезных формул. Это именно те тождества, которые следует хорошенько запомнить. Таблица 4 Десять самых главных тождеств с биномиальными коэффициентами.
|
