Курсовая работа. Биномиальные коэффициенты

• Название: Биномиальные коэффициенты
• Дата: 19.09.2018
• Размер: 0.86 Mb.
• Имя файла: Курсовая работа.doc
• Тип: Курсовая; #51079
• страница: 2 из 5

1.2 Полиномиальная формула

Формула называется

полиномиальной, где суммирование выполняется по всем решениям уравнения в целых неотрицательных числах,Для доказательства выполним умножение

.
Чтобы привести подобные в полученном выражении, необходимо подсчитать количество одночленов вида каждого разбиения. .Для получения же одночлена необходимо выбрать в качестве множителя в скобках при раскрытии выражения. Это можно сделать способами. Из оставшихся не раскрытых скобок необходимо выбрать в качестве множителя вскобках. Это можно сделать способами и т.д. Тогда количество одночленов при раскрытии выражения



будет равно числу упорядоченных разбиений.

1.2.1.Бином Ньютона

Частный вид полиномиальной формулы

(x+y) = C x y + C x y +.....+  C x y +.....+  C x y   (1.1)

где С= или (1.2) где . Эту формулу часто называют биномиальной теоремой, а числа Cи - биномиальными коэффициентами. Равенство (1.1) и (1.2) часто называют биномом Ньютона. Заслуга Ньютона состоит в том, что он обобщил эту формулу для нецелого показателя n.

Доказательство формулы Ньютона можно провести несколькими способами.

Самый традиционный способ - доказательство с помощью метода математической индукции.

Описать метод можно следующим образом:

База индукции. Проверить истинность утверждения для 1.

Шаг индукции. Положить, что утверждение истинно для всех натуральных чисел меньших или равных n.

Индукционный переход. На основании предположения показать, что утверждение истинно и для n+1.

Биномиальная теорема описывает n-ую степень суммы (x+y):

(1.2)

где:


Для доказательства нам понадобится два важных свойства этих чисел

(называемых биномиальными коэффициентами):
(1.3.1)

(1.3.2)
Проведем доказательство по предложенной схеме. Для начала покажем истинность (2) для 1:



Теперь предположим, что (2) истинно, для всех m ≤ n:

(1.5)

Помножим левую и правую части (5) на (x+y) и раскроем скобки: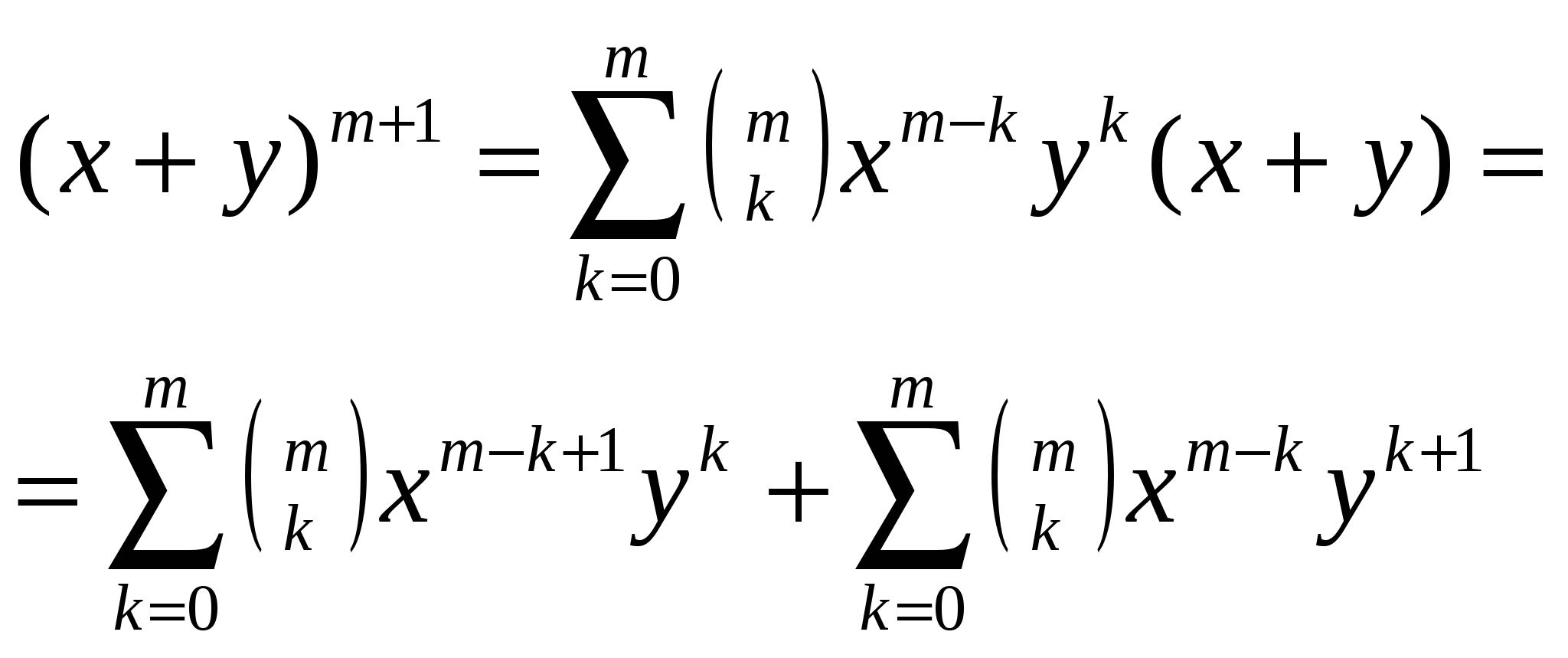


Вынесем первый элемент из первой суммы и последний из второй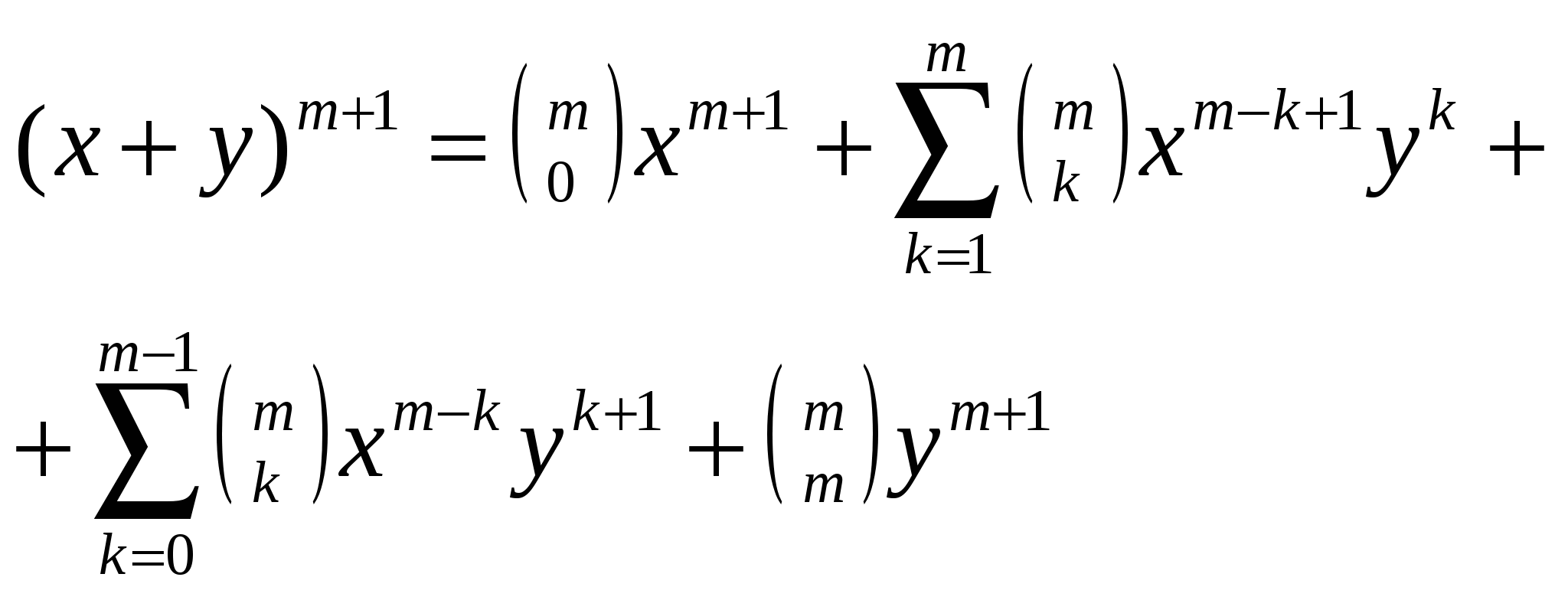




Не трудно видеть, что можно сложить первую и вторую суммы, пользуясь свойством биномиальных коэффициентов (1.3.1)



Мы доказали, что утверждение верно для следующего за n натурального числа, следовательно оно верно для всех натуральных чисел. Теорема доказана.

Второй способ основан на методе производящих функций.
Докажем формулу (1.1) для частного случая: x = 1, y = m, т.е докажем формулу:

(1+x)=1+ nm + n(n-1)m²/2! + n(n-1)(n-2)m³/3! +....+ m  (1.6)

Обозначим коэффициенты в разложении (1+m) при степенях x через B, B, B, ...B, т.е

(1+m)= B + Bm + Bm +...+ Bm  (1.7)

Подставив в записи (1.7)  x=0, найдем значение B=1. Возьмем затем производную от обоих частей равенства (1.7), то получим:  n(1+m)= B + 2Bm + ...+ nBm (1.8) Отсюда, при x=0 находим B=n. 

Теперь возьмем вторую производную от обоих частей равенства  (1.7), получим: n(n-1)(1+m) =  2B +....+ n(n-1)Bm (1.9)

При x=0 получаем B = n (n-1) / 2 и т.д.  На k-том шаге при вычислении k-й производной для равенства (7), получим B = (n (n-1)(n-2)....(n-k)) / k! ,  ч.т.д.