Курсовая работа. Биномиальные коэффициенты

• Название: Биномиальные коэффициенты
• Дата: 19.09.2018
• Размер: 0.86 Mb.
• Имя файла: Курсовая работа.doc
• Тип: Курсовая; #51079
• страница: 3 из 5

Глава 2. Биномиальные коэффициенты

2.1 Понятие биноминальных коэффициентов

Символ — это биномиальный коэффициент, своим названием обязанный биномиальной теореме. В пункте 1.2 мы уже рассматривали интерпретацию биномиальных коэффициентов и вывели формулу подсчета числа сочетаний из n элементов по k мест =С=

Назовем n - верхним индексом, а k- нижним индексом. В соответствии с их комбинаторной интерпретацией эти индексы ограничены неотрицательными целыми числами, так как множества не могут иметь отрицательное или дробное число элементов. Однако биномиальные коэффициенты полезны не только своей комбинаторной трактовкой, а посему от некоторых ограничений будем избавляться. Оказывается, что полезнее всего считать верхний индекс произвольным вещественным (или даже комплексным) числом, а нижний — произвольным целым числом. Соответственно, наше формальное определение принимает следующий вид: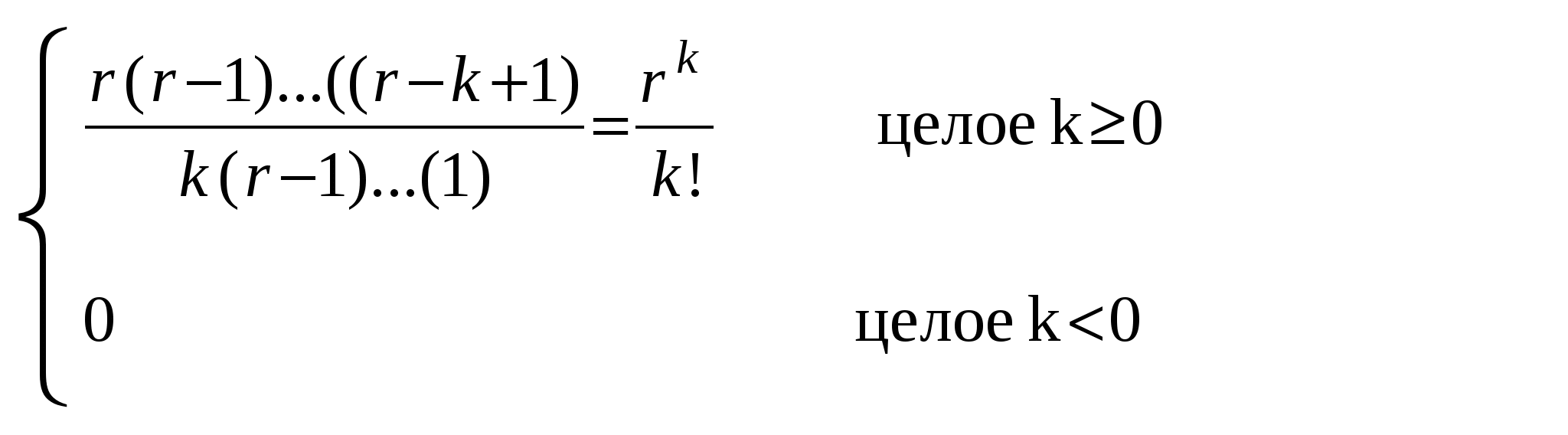

(2.1)

Это определение обладает рядом заслуживающих внимания особенностей. Во-первых, верхний индекс обозначен через r, а не через n- буква r подчеркивает, что биномиальные коэффициенты сохраняют смысл и тогда, когда в этом месте оказывается любое вещественное число. Так,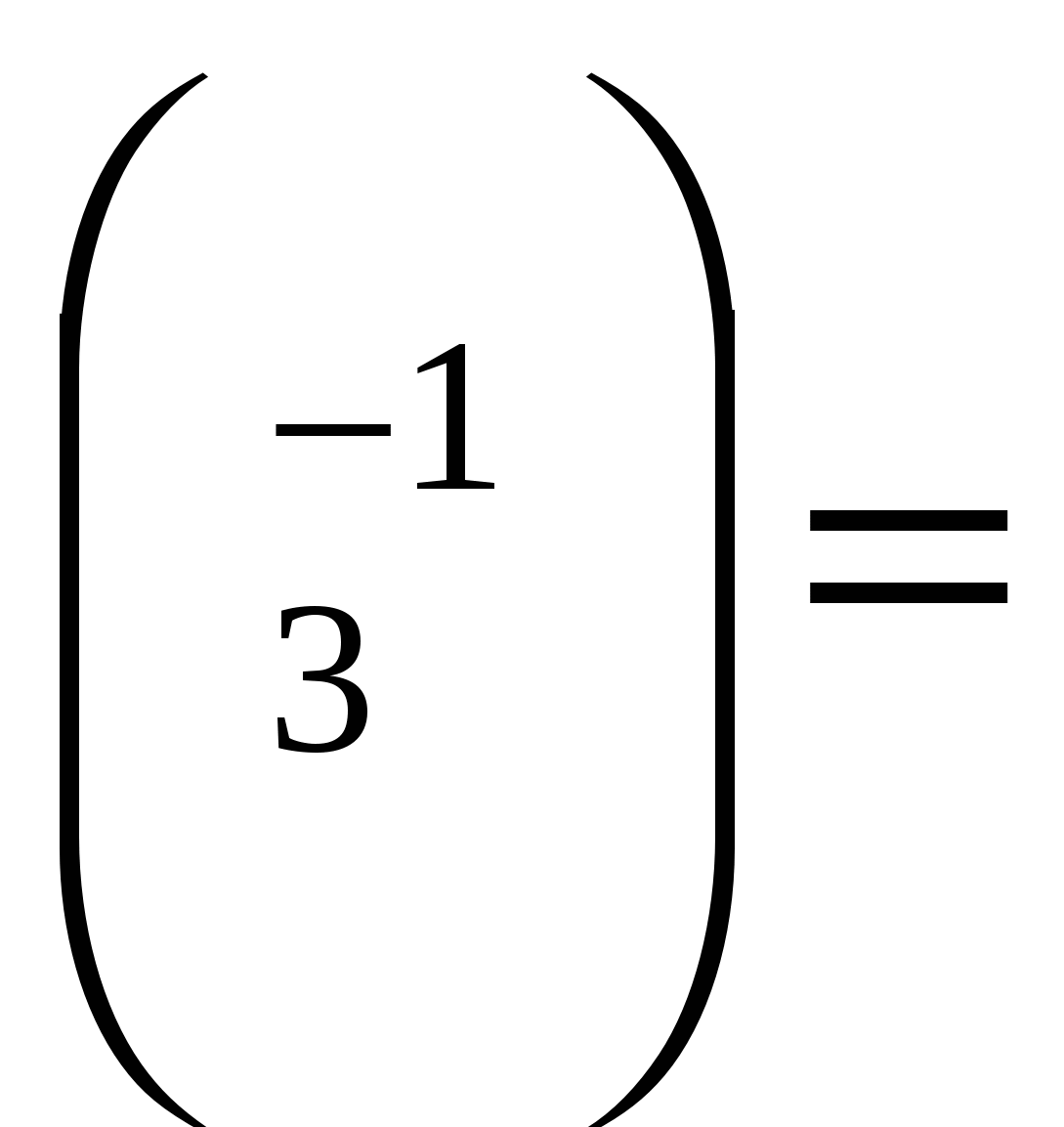

(-1)(-2)(-3)/(3∙2∙1) = -1.

Несмотря на отсутствие комбинаторного смысла, случай r = — 1 оказывается одним из важнейших частных случаев. Некоторые нецелые индексы, типа r = —1/2, также оказываются полезными.

Во-вторых, можно рассматривать как многочлен k-й степени относительно r. Увидим, что такая точка зрения часто бывает плодотворной.

В-третьих, оставим неопределенными биномиальные коэффициенты при нецелых нижних индексах. Можно дать приемлемое определение и в этом случае, но на практике такие коэффициенты редко бывают нужны, поэтому отложим подобное обобщение и займемся им позднее в этой главе.

И последнее. В правой части нашего определения приведены ограничения «целое k ≥ 0 » и «целое k < 0 ». Подобные ограничения будут приводиться во всех рассматриваемых соотношениях с тем, чтобы была ясна область их применимости. Вообще-то, чем меньше ограничений, тем лучше: самое лучшее — соотношение без ограничений; но уж если они присутствуют, то составляют важную часть соотношения. При манипуляциях с биномиальными коэффициентами проще на некоторое время забыть о трудных для запоминания ограничениях, а затем проверить, не были ли они нарушены. Но о проверке забывать нельзя.

Так, практически всякий раз, когда мы сталкиваемся с коэффициентом , он оказывается всегда равен 1. Но внимательное рассмотрение определения (1) показывает, что равен 1 только при n ≥ 0 (при условии, что n целое); если же n < 0, то = 0.

2.2 Основные тождества

Прежде чем приступить к тождествам, которыми будем пользоваться для упрощения биномиальных коэффициентов, обратим внимание на несколько их начальных значений. Числа в таблице образуют начало треугольника Паскаля, названного так по имени Блеза Паскаля 1623-1662),



ТАБЛИЦА 1. Треугольник Паскаля
n




0 1

1 1 1

2 1 2 1

3 1 3 3 1

4 1 4 6 4 1

5 1 5 10 10 5 1

6 1 6 15 20 15 6 1

7 1 7 21 35 35 21 7 1

8 1 8 28 56 70 56 28 8 1

9 1 9 36 84 126 126 84 36 9 1

10 1 10 45 120 210 252 210 120 45 10 1
написавшего о них основополагающий трактат. Пустые места в этой таблице на самом деле означают 0 из-за нуля в числителе (2.1); к примеру, = (1∙2)/(2∙1)= 0. Эти места оставлены пустыми просто для того, чтобы выделить остальную часть таблицы.

Не мешает запомнить формулы для первых трех колонок:

=1, =r, = (2.2)
они справедливы при любом вещественном г. (Вспомните, что =1/2n(n+1)- это формула для треугольных чисел, ; эти числа сразу же бросаются в глаза в колонке таблицы. Неплохо также запомнить около пяти первых рядов треугольника Паскаля: если в какой-нибудь задаче встретится набор чисел 1, 4, 6, 4, 1, то мы можем предположить, что могут быть биномиальные коэффициенты.

Числа в треугольнике Паскаля удовлетворяют практически бесконечному числу тождеств, так что неудивительно, если при его внимательном рассмотрении обнаружим ряд удивительных закономерностей. Вот, например „свойство шестиугольника", которое иллюстрируется шестью числами 56, 28, 36, 120, 210, 126, окружающими число 84 в нижней правой части таблицы. Два варианта перемножения чисел из этого шестиугольника через одно дают одинаковый результат: 56∙36∙210 = 28∙120∙126 = 423360. То же самое справедливо, если выделить подобный шестиугольник из любой другой части треугольника Паскаля.

В обычном случае, когда верхним индексом r является некоторое целое n, большее или равное нижнему индексу k, определению (1) может быть придана иная форма - в виде факториалов:

, целые n ≥ k ≥ 0. (2.3)

Для того чтобы получить эту формулу, просто умножаем числитель и знаменатель (2.1) на (n-k)!. Порой бывает полезно выразить биномиальный коэффициент в подобной факториальной форме (скажем, при доказательстве „свойства шестиугольника"). Но зачастую приходится действовать в обратном направлении, заменяя факториалы биномиальными коэффициентами.

Соотношение симметрии. Факториальное представление указывает на симметричность треугольника Паскаля: каждый ряд читается одинаково - как слева направо, так и справа налево. Тождество, отражающее это свойство,- соотношение симметрии - получается заменой k на n-k:

, целое n ≥0, Целое k (2.4)

Эта формула имеет комбинаторный смысл, ибо определяя k предметов, выбранных из n, тем самым определяем n-k невыбранных предметов.

Ясно, почему n и k в тождестве (2.4) ограничены целыми числами - потому что всякий нижний индекс должен быть целым числом. Но почему n не может быть отрицательным? К примеру, предположим, что n = - 1. Верно ли равенство

?

В частности, при k= 0 в левой части получается 1, а в правой — 0. На самом деле при всяком целом k ≥ 0 левая часть равна

= =

т.е. либо 1, либо -1, но правая часть равна 0, так как нижний индекс отрицателен. А при отрицательном k левая часть равна 0, но правая часть равна

=

т.е. либо 1, либо —1. Так что равенство всегда неверно!

Соотношение симметрии не выполняется и при прочих отрицательных целых n. Но, к сожалению, это ограничение легко забывается, поскольку выражение в верхнем индексе порой бывает отрицательным лишь при некоторых малозаметных (но существующих) значениях его переменных.

Однако этот недостаток соотношения симметрии компенсируется существенным его достоинством: оно выполняется при всех значениях k, даже когда k < 0 или k > n (ибо в таких случаях обе части равны нулю). В случае же, когда 0 ≤k ≤ n, симметрия немедленно следует из (2.3):



Вынесение и внесение из-под знака биномиального коэффициента:

=, целое k ≠ 0 (2.5)

Данное ограничение на k предохраняет нас от деления на нуль. Назовем тождество (2.5) правилом внесения, поскольку, как правило, мы пользуемся им для внесения под знак биномиального коэффициента некоторой мешающей переменной. Это равенство вытекает из (2.1) так как

и k! = k(k- 1)! при k > 0, а при k< 0 обе части равны нулю.

Если умножить обе части (2.5) на k, то получим правило внесения, которое выполняется даже при k = 0:

, целое k. (2.6)
У этого соотношения есть аналог, который сохраняет нижний индекс в неприкосновенности:

, целое k (2.7)

Тождество (2.7) можно вывести из двух соотношений симметрии и одного правила внесения между ними:
(в силу симметрии)
= ( в силу (2.6))
=. ( в силу симметрии)

Данное тождество справедливо при любом вещественном r, а ведь проведенный вывод справедлив, только когда r—целое положительное число. Верхний индекс r-1 должен быть целым неотрицательным числом. Данный вывод справедлив при целом положительном r, и, тем не менее, можно утверждать, что данное

тождество выполняется при всех значениях г в силу того, что обе части (2.7) являются многочленами степени k+1 относительно r. Ненулевой многочлен степени d или меньшей может иметь самое большее d различных нулей - следовательно, разность двух таких многочленов, которая также является многочленом степени d или меньшей, не может обращаться в нуль более чем в d точках, если только она не равна тождественно нулю. Иначе говоря, если два многочлена степени ≤ d совпадают более чем в d точках, то они совпадают во всех точках. Нами показано, что является тождеством всякий раз, когда r-целое положительное число, так что эти два многочлена совпадают в бесконечном числе точек, а значит, тождественно равны.

Способ доказательства из предыдущего абзаца, который мы будем называть полиномиальной аргументацией, полезен при перенесении многих соотношений, справедливых для целых чисел, на вещественные числа - мы неоднократно это увидим. Некоторые равенства, типа соотношения симметрии (2.4) не являются тождествами для многочленов, так что не всегда сможем применять этот способ. Тем не менее, многие соотношения имеют нужный вид.

Формула сложения

Самое важное из всех биномиальных тождеств - известное как формула сложения:

, целое k. (2.8)

Если r-целое положительное число, то формула сложения показывает, что каждое число в треугольнике Паскаля есть сумма двух чисел предыдущего ряда - того, что непосредственно над ним, и того, что рядом слева от него. Эта формула применима также при отрицательном, вещественном или комплексном r с единственным ограничением, чтобы k было целым (с тем, чтобы

биномиальные коэффициенты были определены).

Один из способов доказать формулу сложения — предположить, что r-целое положительное число, и воспользоваться комбинаторными соображениями. Вспомним, что — это число всевозможных k-элементных подмножеств, выбранных из r-элементного множества. Если у нас r яиц, среди которых одно тухлое, то имеется способов выбора k яиц. Ровно в случаях результатом этих выборов будут только свежие яйца, а в случаях среди них окажется тухлое яйцо, ибо результатом таких выборов будет k - 1 из r - 1 свежих яиц. Складывая два этих числа, получаем (2.8). В этом выводе предполагается, что r-целое положительное число и что k ≥ 0. При k < 0 обе части данного тождества равны нулю, а во всех остальных случаях справедливость тождества (2.8) устанавливается путем полиномиальной аргументации.

Тождество (2.8) можно также вывести, складывая два правила внесения-вынесения (2.7) и (2.6):



левая часть – это , следовательно, можно разделить обе части на r. Этот вывод справедлив при всех r за исключением случая r = 0, который легко проверить отдельно.

Еще можно было вывести (2.8) путем непосредственного манипулирования с исходным определением. Если k > 0, то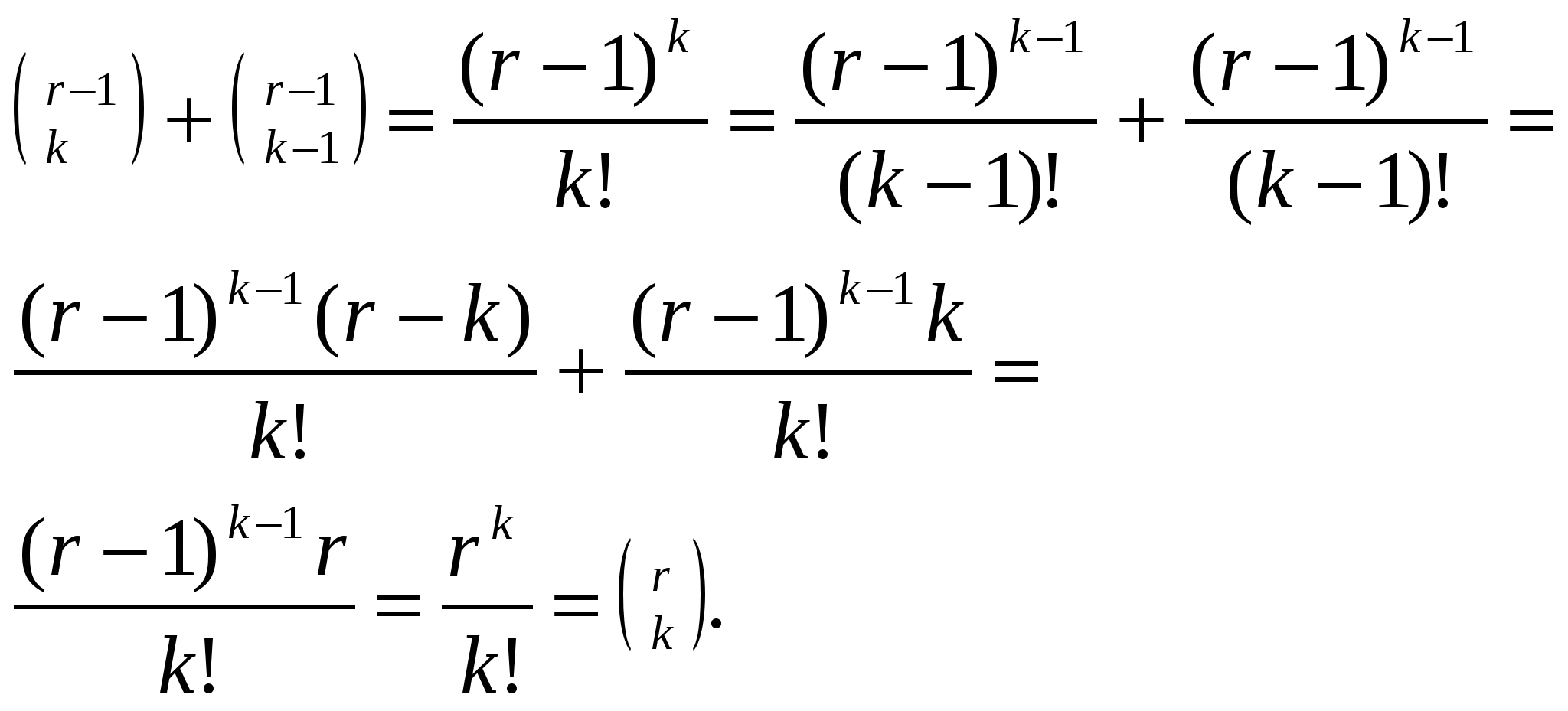



И опять случаи при k≤ 0 легко проверить отдельно.

Мы только что познакомились с тремя весьма различными доказательствами формулы сложения. И это не удивительно: биномиальные коэффициенты обладают большим разнообразием свойств, различие которых обязано приводить к различным доказательствам интересующего нас соотношения.

В сущности, формула сложения — это рекуррентность для чисел из треугольника Паскаля, и мы еще увидим, что она особенно полезна при доказательстве других тождеств по индукции.

А можно и немедленно получить новое тождество, развертывая данную рекуррентность. Так,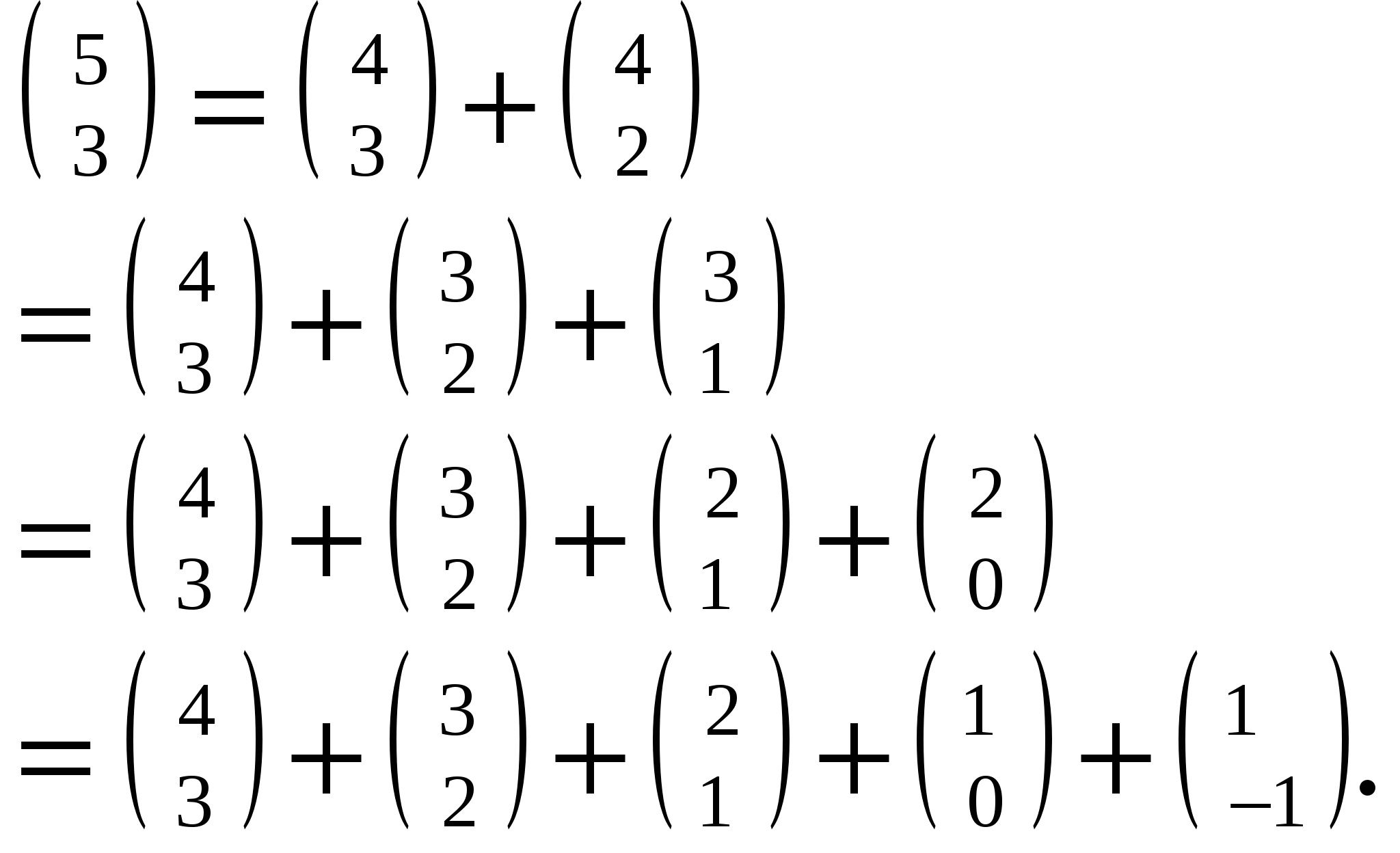


Поскольку = 0, последний член пропадает и можно остановиться. Этот метод дает общую формулу:

целое n. (2.9)

Обратите внимание, что нет необходимости ограничивать индекс суммирования снизу, поскольку все члены суммы при к < 0 равны нулю.

Эта формула выражает один биномиальный коэффициент в виде суммы других, верхний и нижний индексы которых остаются „равноудаленными". Мы нашли ее путем последовательного разложения биномиальных коэффициентов с наименьшим нижним индексом: вначале коэффициента 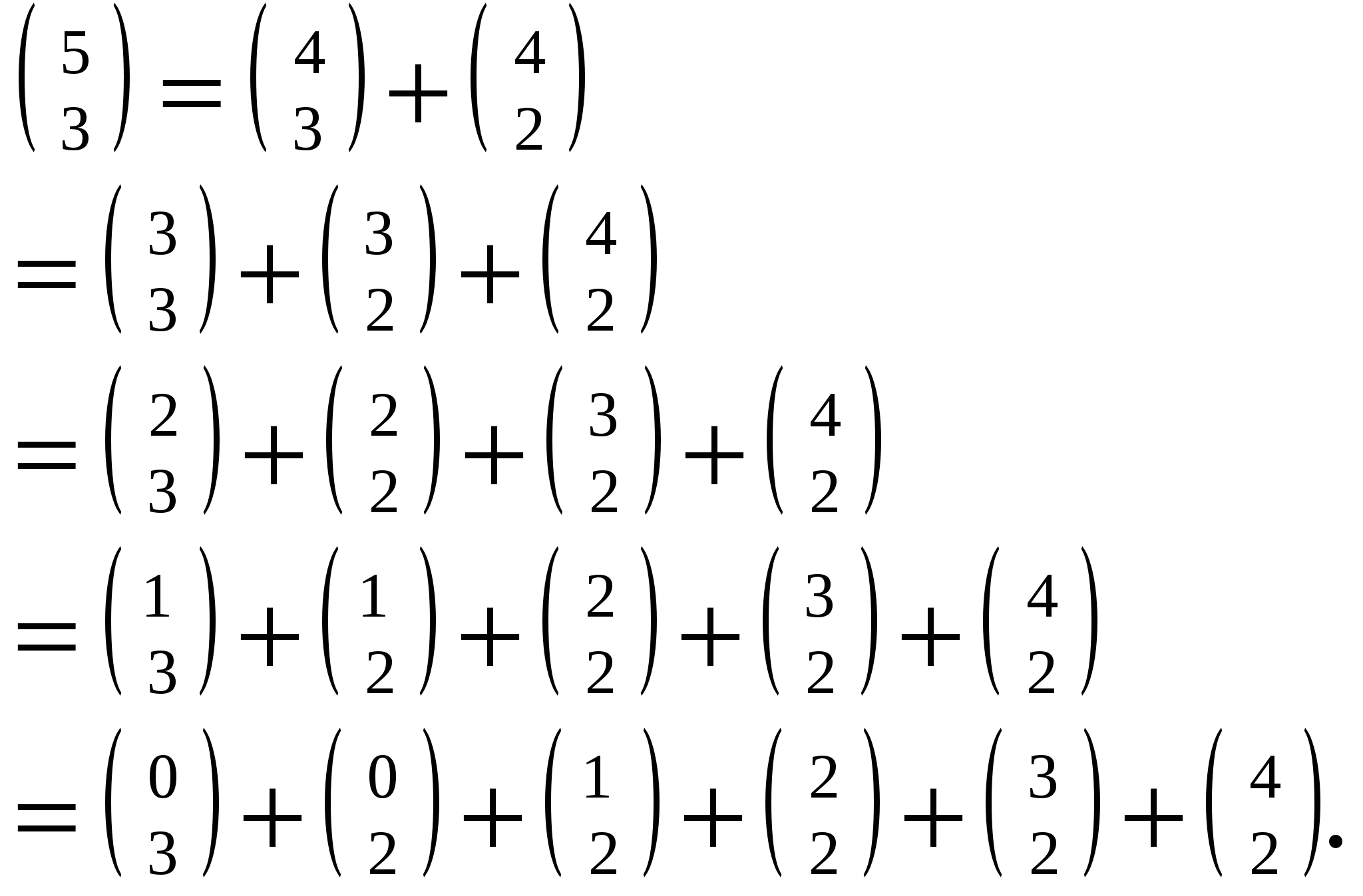, затем коэффициента , потом коэффициента и, наконец, коэффициента . А что случится, если развернуть другим способом - последовательно разлагая коэффициенты с наибольшим нижним индексом? Посмотрим:


Теперь коэффициент равен нулю (так же, как и , хотя они и придают данному соотношению некоторую привлекательность), и можно уловить общую закономерность:

Это тождество, которое мы назовем формулой суммирования по верхнему индексу, выражает один биномиальный коэффициент в виде суммы других, нижние индексы которых не изменяя изменяются. В данном случае сумма нуждается в нижней границе k ≥ 0, так как члены суммы с k < 0 не нули. К тому же m и n вообще не могут быть отрицательными.

Тождество (2.10) допускает интересную комбинаторную трактовку. Если нужно выбрать m + 1 из n + 1 билетов, пронумерованных числами от 0 до n, то это можно сделать способами, если наибольший номер выбранного билета равен k.

Как соотношение (2.9), так и соотношение (2.10) можно доказать по индукции, используя формулу сложения, но можно также получить одно соотношение из другого. Например,

получим (2.9) из (2.10): доказательство послужит иллюстрацией некоторых стандартных операций с биномиальными коэффициентами. В общих чертах план действия таков: сначала преобразовать левую часть соотношения (2.9) таким образом, чтобы она выглядела как левая часть соотношения (2.9); затем прибегнуть к помощи последнего соотношения, заменив всю сумму одним-единственным биномиальным коэффициентом; наконец, привести этот коэффициент к виду правой части (2.9).

Для удобства предположим, что r и n —целые неотрицательные числа; в общем случае соотношение (2.9) будет получаться из этого частного случая в соответствии с полиномиальной аргументацией. Условимся писать m вместо г потому, что эта переменная больше напоминает целое неотрицательно число. Теперь можно приступить к систематическому воплощению нашего плана: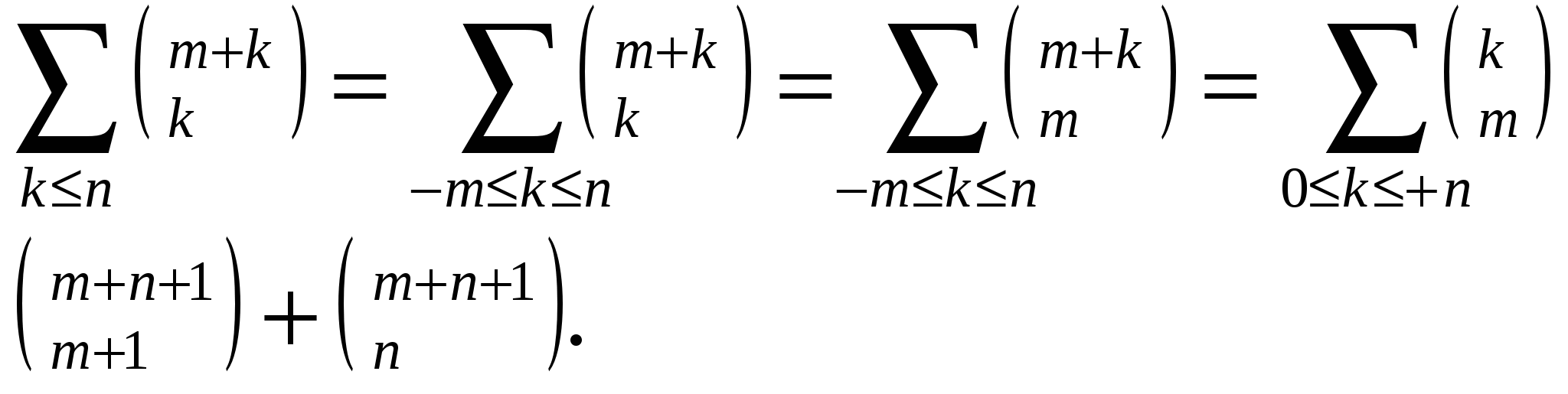



Шаг за шагом проследим за этим выводом. Решающий шаг сделан во второй строке, где мы применяем правило симметрии (2.4) ,чтобы заменить на .

А это можно сделать только при m+k ≥ 0, так что первый шаг ограничивает область изменения k, отбрасывая члены суммы с k< -m (что законно, поскольку отброшенные члены равны нулю). Теперь мы почти готовы применить (2.10): заменяя k на k-m и приводя в порядок диапазон суммирования. Этот шаг, подобно первому. Но теперь k появляется в верхнем индексе, да и пределы суммирования приведены в надлежащий вид, так что в четвертой строчке применяется (2.10). В завершение всего еще раз используется правило симметрии.

Некоторые суммы, на самом деле являются либо частными случаями соотношения (2.10), либо скрытыми вариантами этого соотношения. К примеру, случай m = 1 доставляет сумму неотрицательных целых чисел до n включительно:



А общий случай эквивалентен правилу

, целые m, n≥0,

если разделить обе части этой формулы на m!. И в самом деле, формула сложения (2.8) указывает, что

,

если заменить r и k соответственно на х + 1 и m. Следовательно, методы обеспечивают нас удобной формулой неопределенного суммирования:

(2.11)
Мы уже знаем из предыдущей главы ,что названием биномиальные коэффициенты обязаны биномиальной теореме, которая имеет дело со степенями бинома х + у. Вот простейшие случаи этой теоремы:

(х + у) =1xy,

(х + у) = 1ху +1хy,

(х + у) = 1ху+2хy +1хy,

(х + у) = 1ху +3xy +3xy+1ху,



Нетрудно понять, почему эти коэффициенты совпадают с числами треугольника Паскаля. Когда мы расписываем произведение n сомножителей каждый его член сам является произведением n сомножителей х и у. Число таких членов с k сомножителями х и n-k сомножителями у после приведения подобных членов становится коэффициентом при . А это в точности равно числу способов выбора k из n двучленов, из которых в произведение войдет х, т.е. это .

В некоторых учебниках величину 0° оставляют неопределенной, объясняя это тем, что функции х и 0имеют различные пределы, когда х стремится к 0. Но это заблуждение. Необходимо определить х= 1 при любом х, с тем чтобы биномиальная теорема была верна при х = 0, у = 0 и/или х = -у. Эта теорема слишком важна, чтобы ее произвольно ограничивать! И, напротив, функция 0 совсем не важна.

Биномиальная теорема выступает следующим тождеством:
целое r ≥0 или x/y <1. (2.12)
Это сумма по всем целым k, но в действительности при целом неотрицательном r это конечная сумма, поскольку все ее члены равны нулю, за исключением членов с 0 ≤ k ≤ r. С другой стороны, биномиальная теорема верна и при отрицательном r и даже при произвольном вещественном или комплексном r. В таких случаях данная сумма действительно бесконечна и требуется, чтобы <1 для гарантии абсолютной сходимости суммы.

Два частных случая биномиальной теоремы заслуживают особого внимания, несмотря на то, что они исключительно просты.

Если х = у = 1 и r =n неотрицательно, то

целое n ≥ 0.

Это равенство показывает, что сумма чисел n-го ряда треугольника Паскаля равна 2. А если х вместо +1 равен -1, то

целое n ≥ 0.

К примеру, 1-4 + 6 - 4+1 =0; если снабдить элементы n-го ряда чередующимися знаками, то их сумма равна нулю, за исключением верхнего ряда (когда n = 0 и 0= 1).