РОССИЙСКАЯ ФЕДЕРАЦИЯ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
имени академика И.Г. Петровского
Филиал в г. Новозыбкове
Кафедра математики, физики и информатики
Курсовая работа
на тему:
«БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ»
Выполнила:
студентка 402 группы
Сторожева В.Ю.
Научный руководитель:
старший преподаватель
Савичева Г.В.
Новозыбков 2009
Оглавление
Введение 4
Глава 1. Комбинаторные схемы 6
1.1 Расстановки без повторений 6
1.1.1. Правило суммы 6
1.1.2. Правило прямого произведения 7
1.1.3. Размещение без повторения 7
1.1.4. Перестановки 7
1.1.5. Сочетания 8
1.2 Полиномиальная формула 9
1.2.1.Бином Ньютона 9
Глава 2. Биномиальные коэффициенты 12
2.1 Понятие биноминальных коэффициентов 12
2.2 Основные тождества 14
Заключение 36
Список литературы 37
Приложение 39
Введение
Комбинаторика – раздел математики, в которой изучаются вопросы о том, сколько различных комбинаций, подсчитанных тем или иным условиям, можно составить из заданных объектов.
Комбинаторика становится наукой лишь в XVII веке – в период, когда возникла теория вероятности. Чтобы решать теоретико-вероятностные задачи, нужно было подсчитывать число различных комбинаций, подсчитанных тем или иным условием. После первых работ , выполненных в XVI в. итальянскими учеными Дж.Кардано, Н.Тартальей и Г.Галилеем, такие задачи изучал французский математик Б.Паскаль. В 1665 году был опубликован трактат об «Арифметическом треугольнике», в котором был рассмотрен треугольник Паскаля, популярность чисел составляющих треугольник Паскаля, не удивительна: они возникают в самых естественных задачах алгебры, комбинаторики, теории вероятности, математического анализа, теории чисел.
В нашей жизни мы широко используем раздел математики, называемый комбинаторным анализом. Этот раздел математики изучает так называемые конечные множества. Множества, состоящее из n элементов, называются n –элементными. Однако мы можем выбрать k элементов из n – элементного множества. Каждая k-элементная часть n-элементного множества называется сочетание из n элементов по k . Одна из задач комбинаторного анализа состоит в нахождении числа комбинаций из n элементов по k. Обычно это число обозначается через 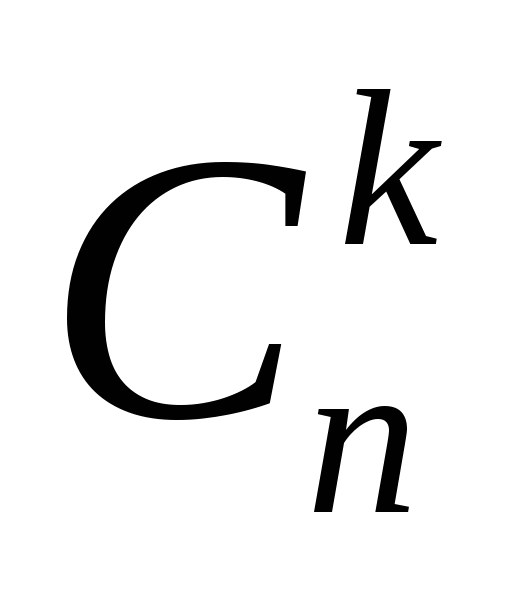 . Это обозначение называют биномиальными коэффициентами, а формулу С . Это обозначение называют биномиальными коэффициентами, а формулу С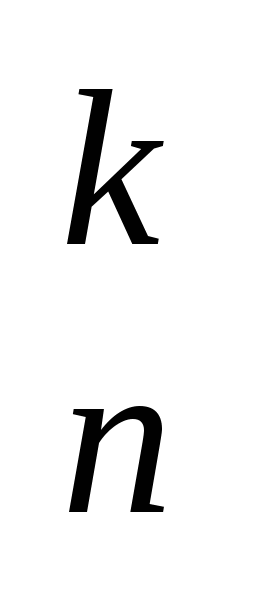 = = 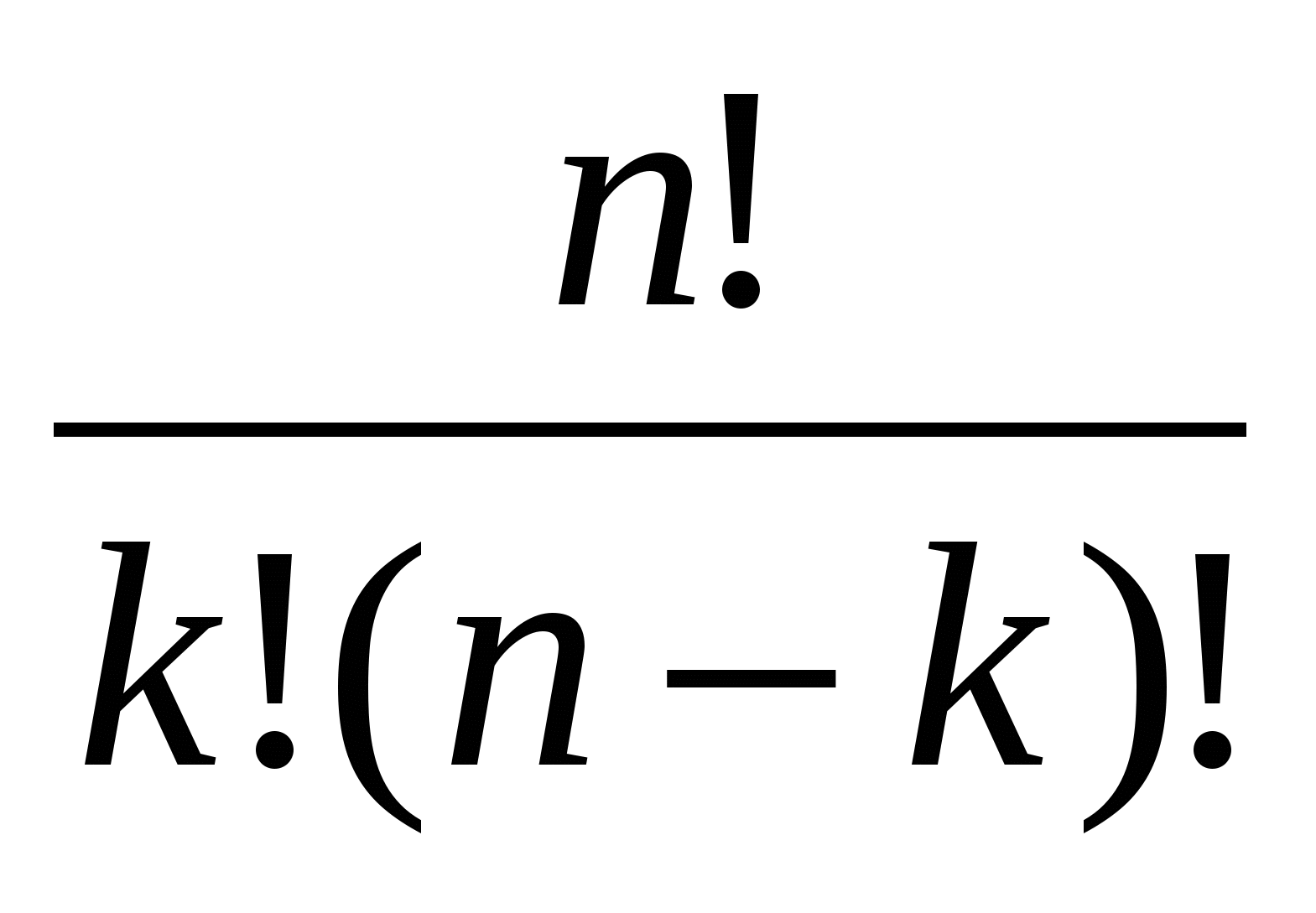 - биномиальной теоремой или Биномом Ньютона. Заслуга Ньютона в том, что он обобщил эту формулу для нецелого показатель n. - биномиальной теоремой или Биномом Ньютона. Заслуга Ньютона в том, что он обобщил эту формулу для нецелого показатель n.
В данной курсовой работе будет сделан обзор комбинаторных формул и биномиальных коэффициентов, наиболее важных для вычислительных задач.
Цель работы: рассмотреть сравнительно не большое число простых правел, с помощью которых можно решать подавляющее большинство практических задач с биномиальными коэффициентами.
Работа будет полезной для студентов математического факультета при изучении комбинаторных схем и биномиальных коэффициентов.
Глава 1. Комбинаторные схемы
1.1 Расстановки без повторений
Пусть имеются два множества А и В.Рассмотрим все пары элементов при условии, что первый элемент берется из множества A, а второй — из множества B. Полученное таким образом множество называется прямым произведением A B множеств Aи B.Напомним некоторые операции над множествами, которыми время от времени будем пользоваться. B множеств Aи B.Напомним некоторые операции над множествами, которыми время от времени будем пользоваться.
А В={( В={( )| )| , , }-прямое произведение множеств. }-прямое произведение множеств.
А В={ В={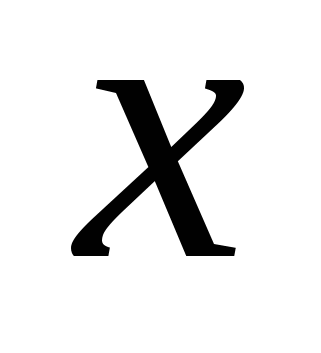 | | } - объединение множеств. } - объединение множеств.
A B B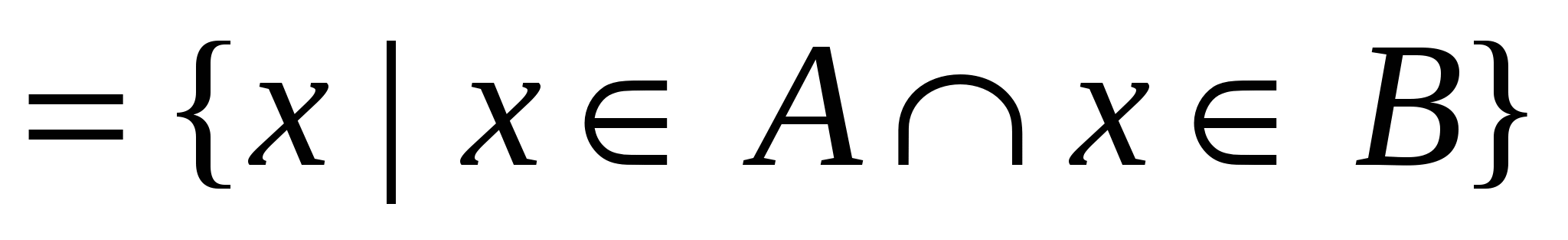 -пересечение множеств. -пересечение множеств.
A\B = 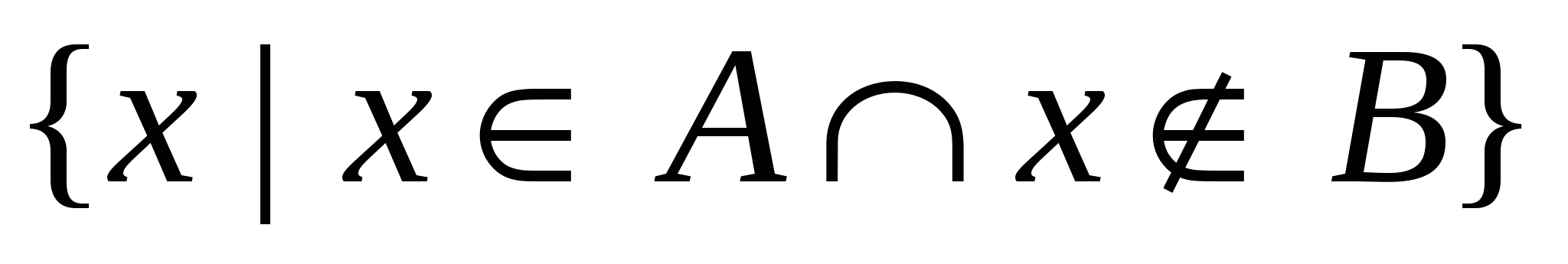 - разность множеств. - разность множеств.
Ø - пустое множество.
U - универсальное множество.
 =UA={x|x =UA={x|x A}-дополнение множества. A}-дополнение множества.
1.1.1. Правило суммы
Пусть Aи B конечные множества такие, что A B=Ø, B=Ø,  и и  . Тогда . Тогда  . .
Интерпретация. Если элемент  можно выбрать mспособами, а элемент можно выбрать mспособами, а элемент  -n способами, то выбор элемента -n способами, то выбор элемента  можно осуществить т + nспособами. Пусть можно осуществить т + nспособами. Пусть — попарно непересекающиеся множества, — попарно непересекающиеся множества,  Ø, где i ≠ j. Тогда, очевидно, выполняется равенство Ø, где i ≠ j. Тогда, очевидно, выполняется равенство 
1.1.2. Правило прямого произведения
Пусть А и В конечные множества,  и и , тогда , тогда . .
Интерпретация.Если элемент можно выбрать mспособами и если после каждого такого выбора элемент можно выбрать mспособами и если после каждого такого выбора элемент  можно выбрать n способами, то выбор пары (a,b) можно выбрать n способами, то выбор пары (a,b) в указанном порядке можно осуществить в указанном порядке можно осуществить  способами. В этом случае говорят, что выбор элементов множества А не зависит от способа выбора элементов множества В. Пусть теперь способами. В этом случае говорят, что выбор элементов множества А не зависит от способа выбора элементов множества В. Пусть теперь — произвольные множества, — произвольные множества, .Тогда .Тогда
Приложение 3.1.
1.1.3. Размещение без повторения
Имеются n различных предметов . Сколько из них можно составить расстановок длины k? Две расстановки считаются различными, если они отличаются видом входящих в них элементов или порядком их в расстановке. Такие расстановки называются размещения без повторений, а их число обозначают А . Сколько из них можно составить расстановок длины k? Две расстановки считаются различными, если они отличаются видом входящих в них элементов или порядком их в расстановке. Такие расстановки называются размещения без повторений, а их число обозначают А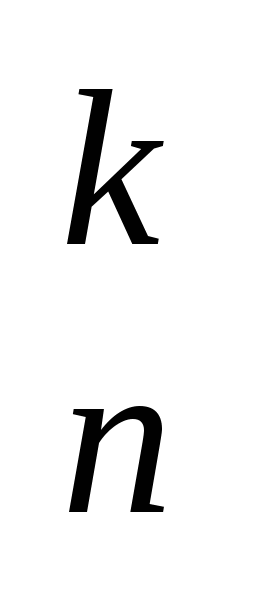 . При составлении данных расстановок на первое место можно Поставить любой из имеющихся nпредметов. На второе место теперь можно поставить только любой из n— 1 оставшихся. И, наконец, на k-е место — любой из п-k+1 оставшихся предметов. По правилу прямого произведения получаем, что общее число размещений без повторений из nпо k; равно . При составлении данных расстановок на первое место можно Поставить любой из имеющихся nпредметов. На второе место теперь можно поставить только любой из n— 1 оставшихся. И, наконец, на k-е место — любой из п-k+1 оставшихся предметов. По правилу прямого произведения получаем, что общее число размещений без повторений из nпо k; равно  Напомним, что Напомним, что  0!=1 0!=1
Приложение 3.2.
1.1.4. Перестановки
При составлении размещений без повторений из n по k; получали расстановки, отличающиеся друг от друга либо составом, либо порядком элементов. Но если брать расстановки, которые включают все n элементов, то они могут отличаться друг от друга лишь порядком входящих в них элементов. Такие расстановки называются перестановками из nэлементов, а их число обозначается P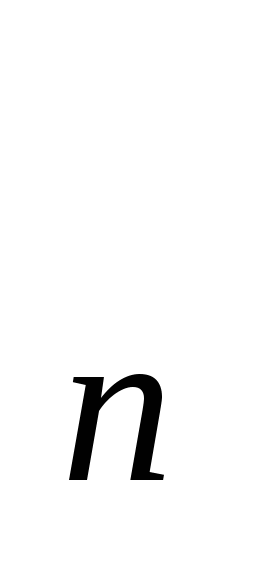 . Следовательно, число перестановок равно . Следовательно, число перестановок равно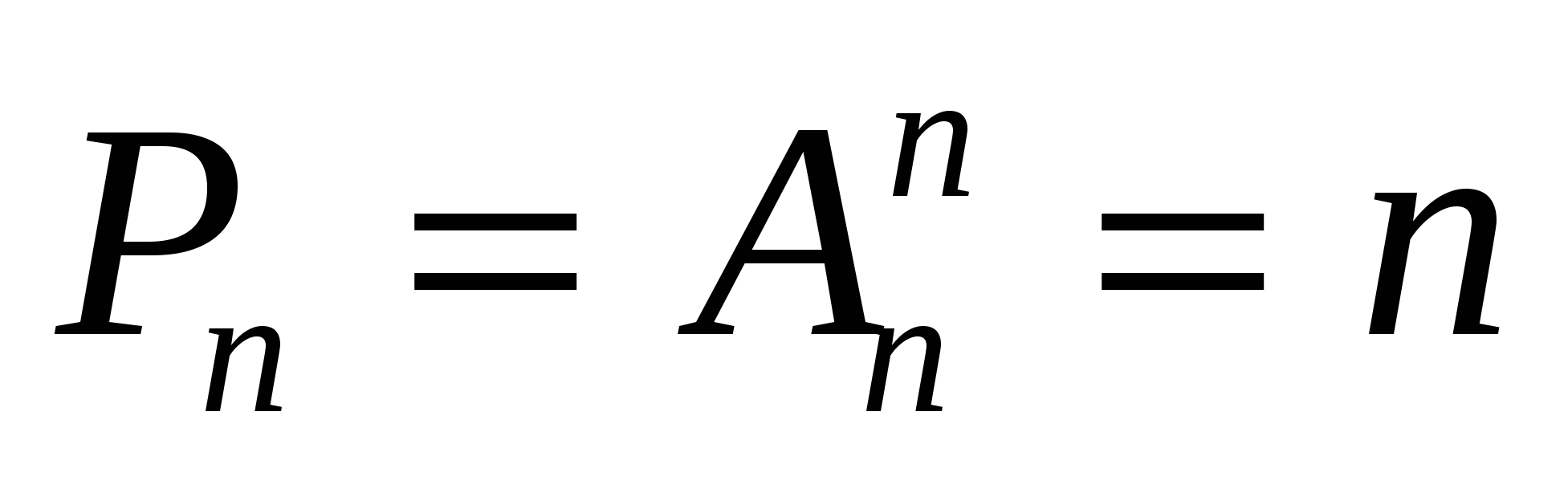 !. Перестановки π=(π !. Перестановки π=(π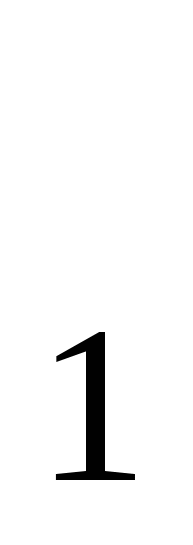 ,π ,π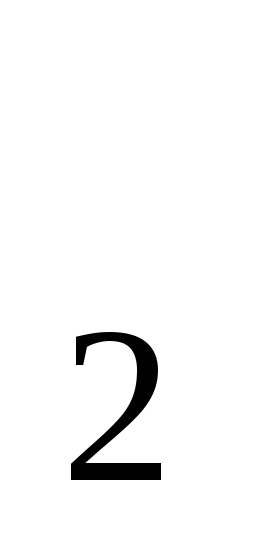 ,…,π ,…,π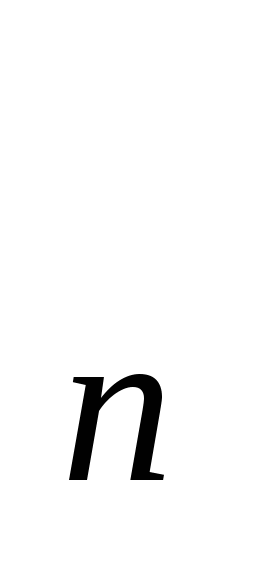 ) элементов 1, 2,..., nзаписывают и в матричной форме ) элементов 1, 2,..., nзаписывают и в матричной форме 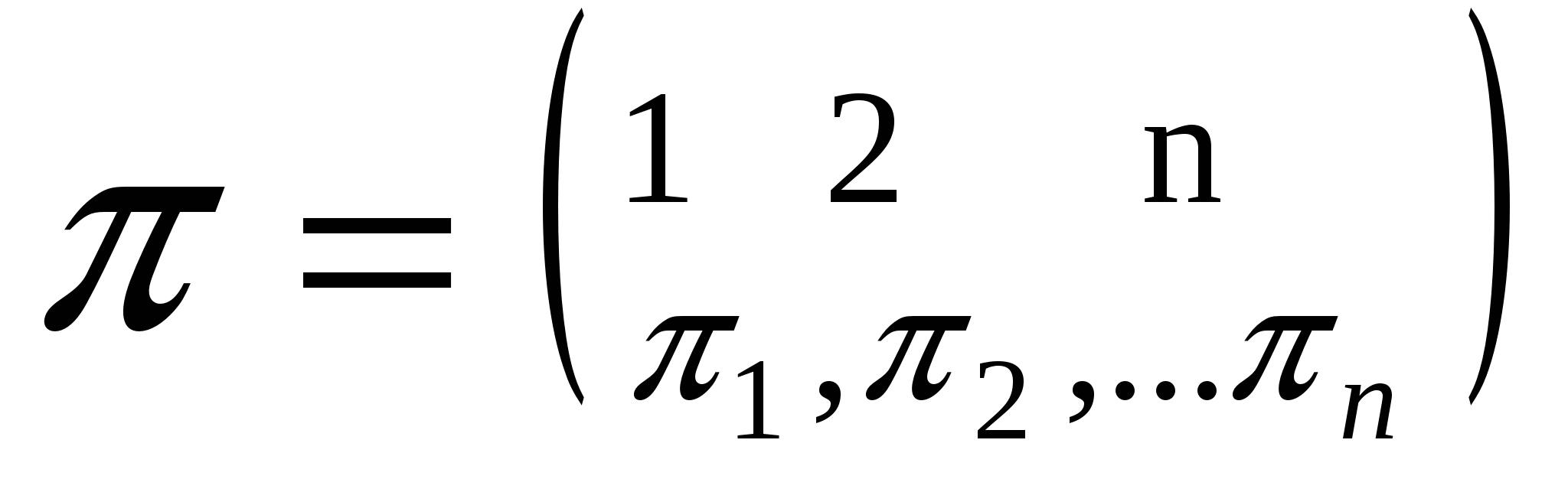 , где верхняя строка — это по рядковые номера 1, 2,..., n позиций элементов в перестановке; нижняя строка — тот же набор чисел 1,2,..., n, взятых в каком-либо порядке; П , где верхняя строка — это по рядковые номера 1, 2,..., n позиций элементов в перестановке; нижняя строка — тот же набор чисел 1,2,..., n, взятых в каком-либо порядке; П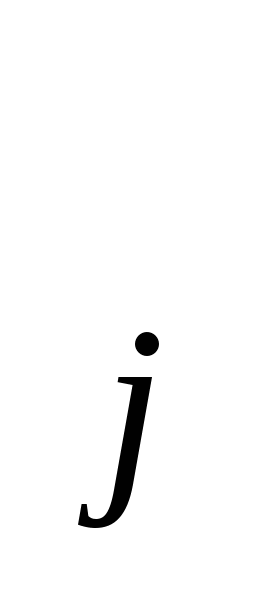 — номер элемента на j-м месте перестановки. Порядок столбцов в перестановках, записанных в матричной форме, не является существенным, так как в этом случае номер позиции каждого элемента в перестановке указывается явно в верхней строке. Например, перестановка (3,2,4,1) из четырех элементов может быть записана как — номер элемента на j-м месте перестановки. Порядок столбцов в перестановках, записанных в матричной форме, не является существенным, так как в этом случае номер позиции каждого элемента в перестановке указывается явно в верхней строке. Например, перестановка (3,2,4,1) из четырех элементов может быть записана как 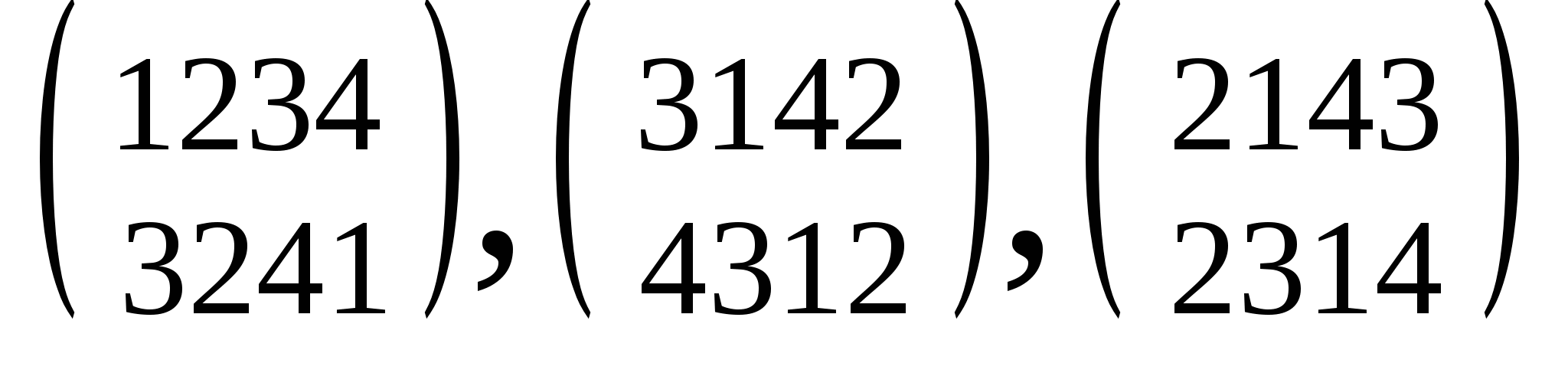 и т.д. и т.д.
Приложение 3.3
1.1.5. Сочетания
В тех случаях, когда не интересует порядок элементов в расстановке, а интересует лишь ее состав, то говорят о сочетаниях. Сочетаниями из nразличных элементов по k; называют все возможные расстановки длины k, образованные из этих элементов и отличающиеся друг от друга составом, но не порядком элементов. Общее число сочетаний обозначают через С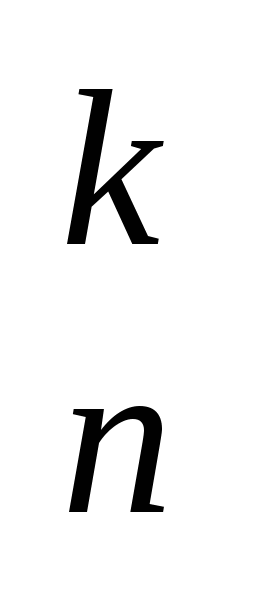 или или 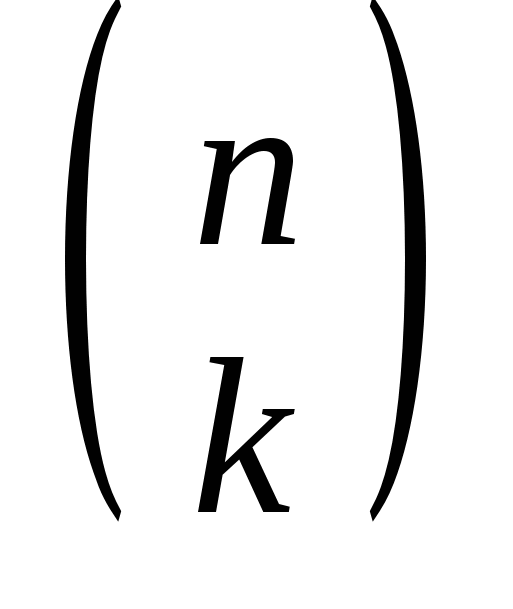 . .
Определим это число. Составим все сочетания из n по k. Затем переставим в каждом сочетании элементы всеми возможными способами. Теперь мы получили расстановки, отличающиеся либо составом, либо порядком, т.е. это все размещения без повторений из n по k. Их число равно А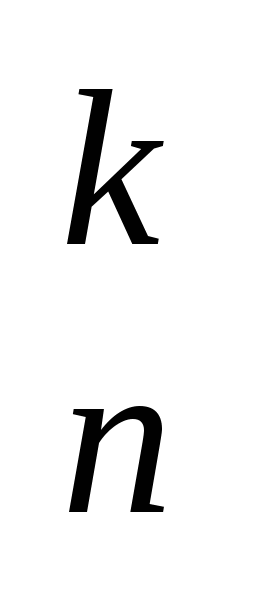 . Учитывая, что каждое сочетание дает k! размещений, то по правилу произведения можно записать . Учитывая, что каждое сочетание дает k! размещений, то по правилу произведения можно записать 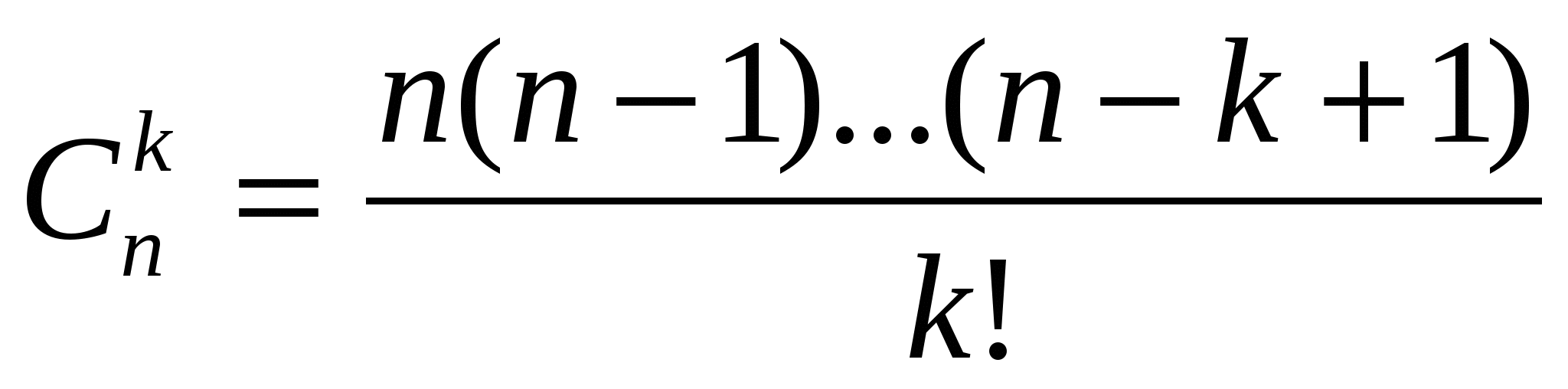 или или 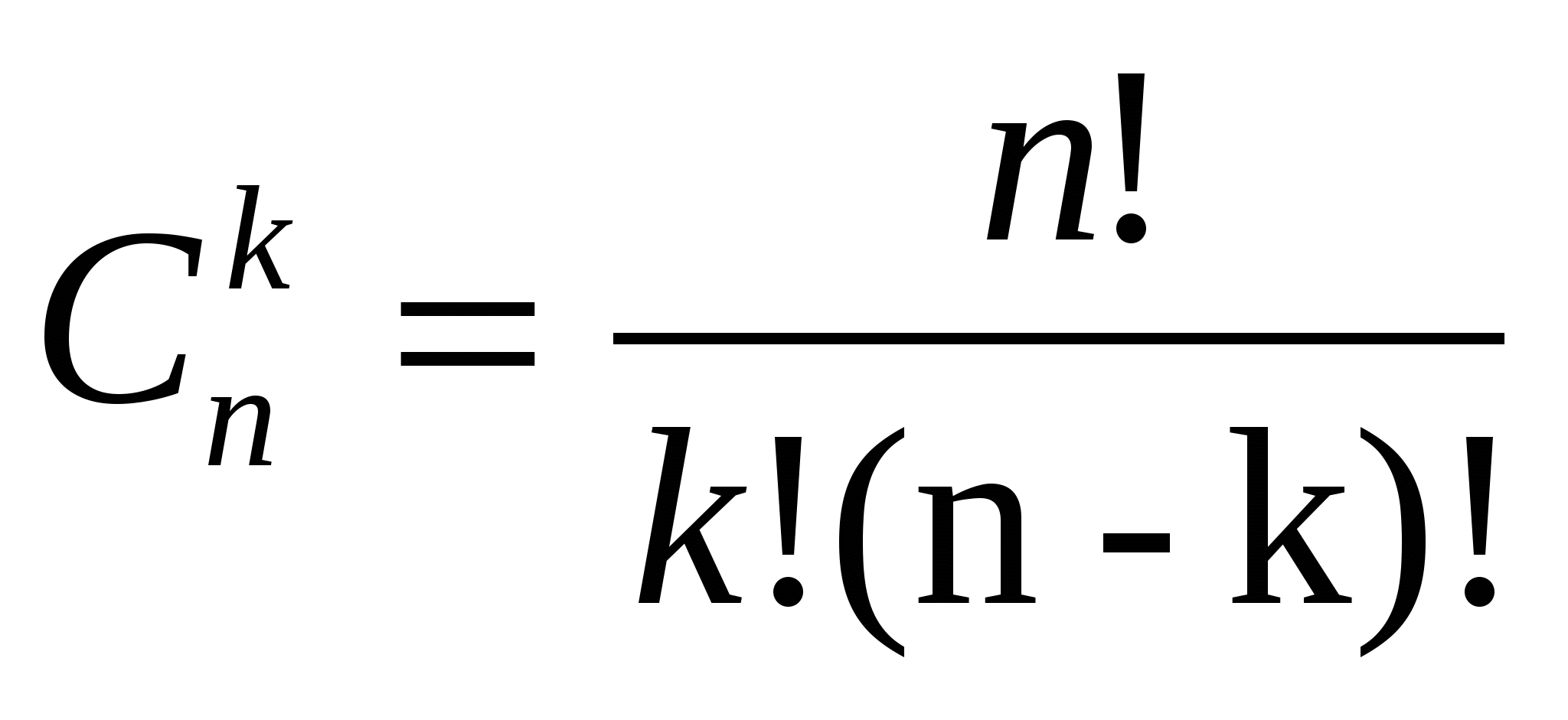 . Тогда . Тогда 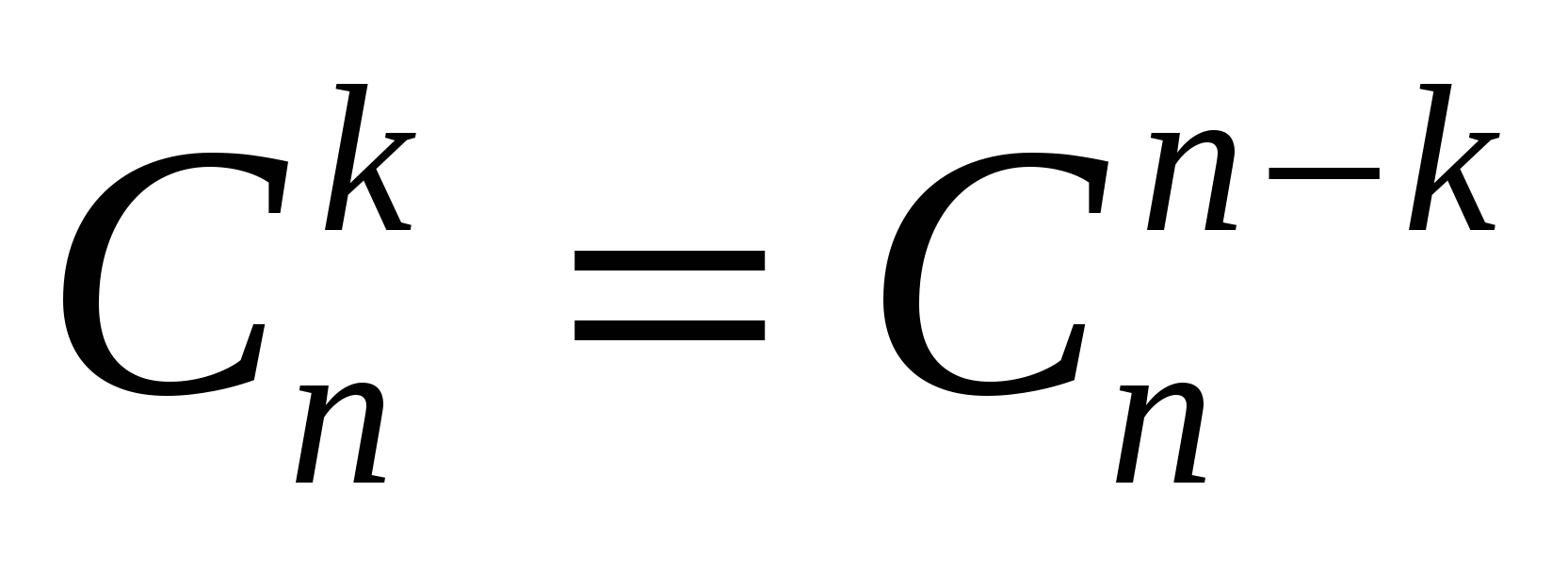
Приложение 3.4.
|
 Скачать 0.86 Mb.
Скачать 0.86 Mb.