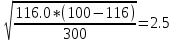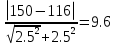Книга БИОСТАТИСТИКА (Автосохраненный). Биостатистика
 Скачать 1.08 Mb. Скачать 1.08 Mb.
|
|
3.6 Оценка и анализ вероятности статистических гипотез. В подразделе|подразделении| рассмотрено понятие «оценивания|оценивание| достоверности полученных результатов», представленные мето ды| расчете погрешностей и критерии оценивания достоверности Госсета (Стьюдента). Вопрос для изучения
Цель: ознакомить с методическими основами|основанием| оценивания достоверности результатов и параметрическими мето дами| расчета достоверности показателей и их разницы|разности|.
Необходимость оценивания достоверности полученных результатов определяется объемом исследования. Она не проводится при сплошном исследовании (для анализа отобраны все возможные единицы наблюдения) поскольку для всей (генеральной) совокупности можно получить только одно значение определенного показателя. Однако в системе| медико-биологических исследований (кроме данных официальной статистики) редко используют сплошные методы сбора информации — подавляющая часть исследований является выборочной|избирательной|.
Изучение любой|какой-нибудь| проблемы, конечно, сопровождается| необходимостью дать ответ на ряд вопросов относительно достоверности полученных результатов:
4) существенная разница|разность| ли между аналогичными показателями| в разных|различных| группах (больных, население и тому подобное). При проведении выборочного|избирательного| исследования мы можем| наталкиваться на общие погрешности и погрешности выборки. Общие погрешности могут иметь как систематический|систематичный| харак тер| (методические, недостатки|недостаток| измерительной аппаратуры), так и случайный (ошибки|ошибка| исследователя). Погрешности выборочного наблюдения связаны|повязал| с отбором его единиц. Это погрешности типичности, репрезентативности. В процессе анализа рассчитанные показатели (средняя длительность лечения, частота осложнений|усложнения|, уровень летальности|, и тому подобное) рассматривают как обобщающие величины|. Если результаты получены на основе достаточного за количеством и качественно однородного материала, то можно считать, что они достаточно точно характеризуют исследуемые явления. Для оценки достоверности результатов любых выборочных исследований определяют среднюю ошибку относительной (mр) или средней величины (mM).
Средняя ошибка для соответствующих показателей при значительном числе наблюдений (n > 30) может быть рассчитана по таким формулам: mx= 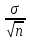 - средняя ошибка средней величины; - средняя ошибка средней величины;m= 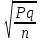 - средняя ошибка относительной величины; - средняя ошибка относительной величины;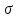 – среднее квадратичное отклонение; – среднее квадратичное отклонение; n – число наблюдений в выборочной совокупности; P – относительный показатель; q – величина обратная показтелю, то есть достоверность того, что данное явление не будет зарегистрировано. Сумма двух противоположных вероятностей равняется единице: Р + q = 1. Если показатель рассчитан на 100 (%), тогда: q = 100 — Р, если на 1000 (%о), то q = 1000 - Р и так далее При малом числе наблюдений (п < 30) в знаменателе| вместо n используется n - 1|.
Доверительные границы|граница| для средних и относительных величин определяют формулами: 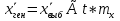 Pген=Pвыб Pген=Pвыб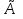 t*mp , где: t*mp , где:
Границы |граница| достоверности (доверительные границы|граница|):
Вероятность безошибочного прогноза и доверительный критерий определяют на этапе планирования статистического исследования. При заданных степенях вероятности доверительный критерий (t) имеет неизменную|неизменяемую| величину, а доверительный интервал зависит от величины средней погрешности (m), значение которой|какой| уменьшается при увеличении числа и качественного состава наблюдений.
В медико-биологических исследованиях часто возникают ситуации, когда при сравнении отдельных параметров необходимо оценить существенность разницы между ними. Существенная разница между отдельными показателями выборочного исследования свидетельствует о возможности перенесения полученных выводов на генеральную совокупность. Критерием оценки существенности разности является коэффициент достоверности (критерий Госсета (Стьюдента), который определяют по формуле: 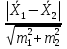 для средних величин; 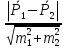 для относительных величин При большом|великом| числе наблюдений (n > 30) разность |разность| между показателями является существенной, если:
При условии t<2| степень достоверности безошибочного прогноза составляет менее|меньше| 95 %. В этом случае мы не можем утверждать, что разница|разность| между показателями является существенной.
Часто при клинических или экспериментальных исследованиях придется иметь дело с малыми наблюдениями (30 и меньше): 5-6 лабораторных ширин, 10-12 больных и тому подобное. Если исследование правильно организовано, отобраны однородные группы, какие можно использовать, как выборочные с малым числом наблюдений. При малом числе наблюдений (п < ЗО) оценки достоверности разницы между параметрами отдельных групп о водится на основе сравнения результата и значений критерия Госсета (Стьюдента), но и итогвыми табличными значениями для соответствующей исчисляй степеней свободы (n`= n1+ n2 - 2) Если определенный t-критерий превышает табличное значение— разница между показателями становится статистически доказана.
Критерий достоверности (t) используют при попар ном| сравнении исследуемых параметров. Однако при проведении статистического анализа иногда необходимо оценить|оценивать| достоверность разницы|разности| большей от двух количеству показателей клинико-статистических| групп. Попарное сравнение их не позволяет получить обобщающую оценку. Иначе необходимо провести сравнение совокуп ности| не только по обобщающим показателям, но и за характером распределения|деления| признаков в исследуемых группах. Для данной цели используют другие критерии, которые|какие| будут рассмотрены дальше. Вопросы для контроля: 1. Что означает выражение «оценить|оценивать| достоверность результатов| исследования»? 2. За какими критериями определяют довесочный интервал|? 3.7. Непараметрические методы оценки вероятности статистических гипотез В подразделе|подразделении| представлены методики расчета и анализа непараметрических критериев оценивания достоверности полученных результатов, рассмотрено понятие независимой и взаимоувязанной совокупности. Вопросы для| изучения: —Как рассчитываются непараметрические критерии оценивания достоверности?
Цель: Ознакомить с понятием независимых и взаимосвязанных по| совокупности, научить адекватно подбирать определен непараметрический критерий для оценивания достоверности разницы|разности| результатов, проанализировать прак тическое| использование|употребление| непараметрических критериев.
Рассмотрены в предыдущих разделах статистические параметры (средняя арифметическая, среднее квадратичное отклонение, коэффициент вариации, средняя ошибка), которые используют для анализа вариационных рядов, являются его параметрами и требуют представления выходных данных в количественном виде. Однако при проведении медицинских исследований достаточно часто придется использовать методы статистического анализа данных, представленных в полуколичественном, полукачественном и качественном виде. Совокупность статистических методов, которые позволяют оценить их результаты как в количественном (числовом), так и в полуколичественном и качественном виде объединяют в группу непараметрических критериев оценивания.
Подавляющее большинство параметрических статистических методик предусматривают наличие нормального распределения|деления| вариант в исследуемой совокупности. Но на практике встречаются не только нормальные, но и другие виды раздела| признаков. При наличии таких ситуаций использование|употребление| параметрических критериев повышает вероятность ошибок|. Практическое|практичное| применение непараметрических кри териев|, не связанное|повязал| с определенной формой распределения|деления| исследуемых признаков, делает целесообразным их самостоятельное использование|употребление| или в комплексе с параметрическими. Невзирая на|несмотря на| определенную простоту методик, надежность непараметрических критериев достаточно высока. Они могут быть использованы для оценивания достоверности медико-биологических результатов одной совокупности, разницы|разности|, двух и больше выборочных|избирательной| совокупностей. |

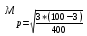 =0,85%
=0,85%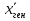 и Pген - значение средних и относительных величин, рассчитанных для генеральной совокупности;
и Pген - значение средних и относительных величин, рассчитанных для генеральной совокупности;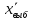 и Pвыб – значение средних и относительных величин, рассчитанных для выборочной совокупности;
и Pвыб – значение средних и относительных величин, рассчитанных для выборочной совокупности;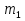 =
=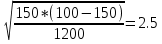
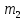 =
=