Книга БИОСТАТИСТИКА (Автосохраненный). Биостатистика

• Название: Биостатистика
• Анкор: Книга БИОСТАТИСТИКА (Автосохраненный).docx
• Дата: 13.03.2017
• Размер: 1.08 Mb.
• Имя файла: Книга БИОСТАТИСТИКА (Автосохраненный).docx
• Тип: Документы; #3728
• страница: 9 из 19

Полный расчет «ожидаемых» чисел летальности в соответствии со стандартом приведен в

таблице 16.
Таблица 16. Расчет «ожидаемых» и стандартизированных показателей (III / IV этап)

Срок госпитализации	Уровень летальности %		Раздел больных по стандарту	Уровень летальности по стандарту
	А	Б		А	Б
До 6	12,2	10,0	34,1	4,2	3,4
6-24	17,6	16,6	31,8	5,6	5,3
После 24	28,6	27,9	34,1	9,8	9,5
Всего	16,6	25,0	100,0	19,6>18,2

IV этап — вычисление стандартизированных показателей. На этом этапе находим итог результатов, рассчитанных на предыдущем этапе по всем группами для соответствующих больниц. Сумма «ожидаемых» чисел и есть стандартизованные по срокам госпитализации показатели частоты летальности для обеих больниц.

Они составляют: для больницы А — 19,6; для больницы Б — 18,2 случаев смертей на 100 госпитализированных больных.

Изменение соотношения между фактическими и стандартизированными показателями свидетельствует о влиянии исследуемого фактора на уровне общих интенсивных показателей.

Вывод. При условиях одинакового состава больных с острой кишечной непроходимостью по срокам госпитализации в обеих больницах уровень летальности был бы выше в больнице А. Высокий фактический уровень летальности в больнице Б, определенный на II этапе, можно объяснить большей частью госпитализированных больных в поздние сроки (свыше 24 часов от начала заболевания). Уровень летальности зависит от состава больных по срокам госпитализации в исследуемой больнице.

Следовательно, алгоритм расчета стандартизированных показателей прямым методом можно изобразить в виде схемы - алгоритма (рис. 14).
Рис. 14. Алгоритм расчета стандартизированных показателей прямым методом


Выбор стандарта и его расчет

Исчисление общих и специальных (групповых) интенсивных показателей (по полу, возрасту, профессии и т.д.)



Исчисление групповых стандартизованных показателей



Сравнение общих интенсивных и общих стандартизированных показателей



Получение общих стандартизированных показателей



Оценка и выводы



Таким образом, стандартизированный показатель демонстрирует, какой была бы заболеваемость (летальность, смертность, инвалидность) в сравниваемых контингентах, если бы их состав был однородным, то есть расхождения в составе контингентов были бы нивелируемыми.

Стандартизированные показатели применяются для сравнения двух показателей, но не отображают настоящие размеры явлений, потому что величина их может изменяться при изменении стандарта.

Таким способом можно установить факт влияния любого фактора на упомянутые показатели и обнаружить причину изменений показателей, которые рассчитываются обычными методами.

Вопросы для контроля:

1. 
   В каких случаях используют стандартизированные показатели?
   
2. 
   В чем заключается практическая значимость метода стандартизации?
   

1. 
   Как проводится оценивание стандартизированных показателей?
   

3.4.Динамические ряды и их анализ.

В подразделе выясняются основные понятия о рядах динамики, их показателях и методах выравнивания.

Вопросы для изучения:

• 
  Что такое динамический ряд?
  
• 
  В чем заключается суть его выравнивания?
  
• 
  Где используются динамические ряды?
  

Цель: ознакомить с расчетом показателей динамического ряда и методикой их выравнивания, продемонстрировать значения анализа динамических рядов в медицине.

Отдельные явления или параметры, которые изучаются разными областями медицинской науки и практики, в течение времени часто изменяют свою интенсивность. Эти изменения сказываются на развитии явлений. Поэтому при их изучении необходимо учитывать величину и направление изменений. Особенно большое значение для практического здравоохранения имеет информация об изменениях характерных демографических процессов, заболеваемости населения, деятельности учреждений здравоохранения, и др. Адекватность направленности и реализации практических рекомендаций и мероприятий в значительной мере зависит от правильного оценивания их характера. Поскольку такие изменения часто являются следствием практических оздоровительных мероприятий, анализ их позволяет оценить эффективность проводимой работы.

Для здравоохранения практический интерес имеет и тенденция развития некоторых явлений. Оценивание ее на данный момент часто позволяет предусмотреть изменения в будущем и соответственно наметить и принять необходимые практические меры.

Процесс развития изменений отдельных явлений (в том числе, медико-социальных) по времени в статистике принято называется динамикой, для отображения которой строят соответствующие ряды.

Динамический ряд – это ряд статистических величин, которые воспроизводят изменения явления во времени и расположенны в хронологическом порядке через определенные промежутки времени.

Составляющими частями динамического ряда являются его уровни и интервалы - показатели времени (годы, кварталы, месяцы, и так далее) или моменты (периоды времени). В зависимости от того, как уровни ряда отображают состояние явления, динамические ряды по своему виду могут быть:

Уровни ряда – это величины, из которых состоит динамический ряд – размер того или другого явления, достигнутый в течение определенного периода или на определенный момент времени.

• моментными — величины ряда характеризуют явление на какой -то определённый момент времени (штаты, койки на конец календарного года, выявленные больные при медицинском осмотре);

• 
  интервальными — уровни ряда определяют за определенный период времени (число случаев госпитализации в стационар, число летальных случаев на протяжении года, число вызовов скорой помощи на протяжении суток).
  

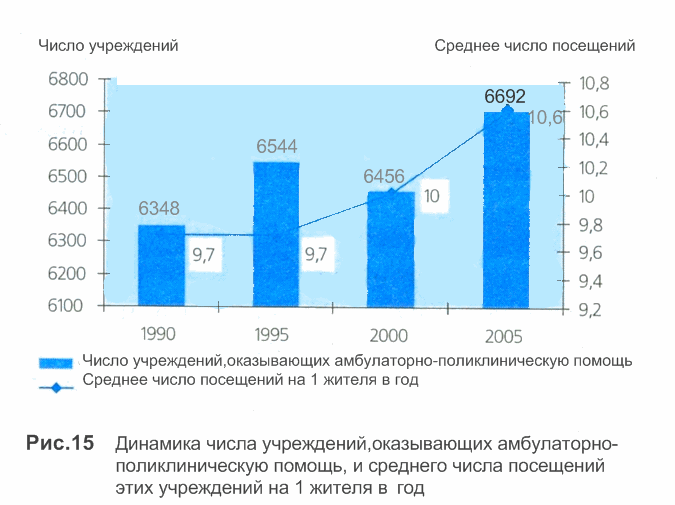На рис. 15 приведены примеры моментного и интервального ряда.

Для разных по характеру интервальных и моментных динамических рядов обнаруживают некоторые особенности уровней. Поскольку уровнями интервального ряда является суммарный размер явления за определенный промежуток времени, то они зависят от длительности данного периода времени и могут быть представлены как итог. В моментных рядах уровни содержат элементы повторного подсчета (например, численность населения Украины по данным переписей), потому подытожить их невозможно.

Величины, которые изучают в динамике (уровни ряда), могут быть представлены в виде:

• 
  абсолютных чисел;
  
• 
  относительных (интенсивные показатели, соотношения);
  
• 
  средних величин.
  

Для анализа динамики не всегда целесообразно использовать абсолютные величины, поскольку их изменение достаточно часто связано с изменением численности среды или основы для формирования. Например, уменьшение числа случаев госпитализации к стационару может быть связано с сокращением коечного фонда за определенный промежуток времени, а не с фактическими показателями здоровья населения. Рассмотрение в динамике экстенсивных показателей (структуры) у большинства случаев является нецелесообразным и может быть проведен только в особенных случаях, при условии четкой интерпретации и обязательного учета изменений в структуре всей совокупности.

По данным критериям динамические ряды можно разделить на ряды абсолютных, относительных и средних величин (простые и сложные).

В зависимости от расстояния между уровнями динамические ряды можно разделить на равноудаленные (равномерные интервалы между датами) и неравноудалённые (неравномерные промежутки или прерванные периоды).

Характер основной тенденции исследуемых процессов, представленных в виде динамических рядов, делит их на стационарные и нестационарные. Если математически ожидаемые (прогнозируемые) значения признаков и параметры их стабильности (среднее квадратичное отклонение, коэффициент вариации) являются постоянными, не зависят от времени, то такой процесс является стационарным. Данные ряды также называются стационарными. Медико-социальные процессы по времени, конечно, не является стационарными, поскольку каждый из них содержит в себе определенную тенденцию развития.

Важным условием правильного построения динамически го ряда и его последующей характеристики есть возможность сопоставления его отдельных уровней. Сравнивая данные в динамике, необходимо всегда помнить о территориальном и качественном сопоставление результатов. Основными причинами, которые усложняют или делают невозможным составление уровней динамического ряда, является:

• изменение единиц измерения или подсчета (оценивание экономической эффективности работы лечебно-профилактических учреждений в разных денежных эквивалентах за определенные периоды — рубли, купоны, гривны, у.е.);

• 
  неравномерная периодизация динамики (количественная — по годам, качественная — по социально-экономическими периодам, изменениям приоритетности разных типов учреждений в структуре лечебно-профилактической помощи);
  
• 
  изменение перечня объектов анализа (переход ряда лечебно -профилактических учреждений с одного подчинения другому);
  

• изменение территориальных пределов областей, районов, и др.

При наличии вышеуказанных условий проблему решают в процессе сбора и обработки данных или путём их пересчета.

Методы медицинской статистики позволяют измерять размеры изменений, которые состоялись в течение определенного периода времени, и количественно охарактеризовать направленность их развития. С данной целью используют такие показатели: абсолютный прирост, темп роста, темп прироста.

Абсолютный прирост – это разница между данным уровнем ряда и тем, что принятый за основу (предыдущим, начальным) Темп роста – отношение данного уровня ряда до уровня, принятого за основу, определенное в процентах. Темп прироста – отношение абсолютного прироста за данный период времени до абсолютного уровня предыдущего периода, определенное в процентах. Абсолютное значение 1% прироста – отношения абсолютного прироста к темпу прироста.

Абсолютный прирост может быть как позитивным, так и негативным. Он отображает, на сколько единиц, в абсолютном выражении изменился уровень, того или иного периода в сравнении с базовым. Один и тот же абсолютный прирост относительно разных исходных уровней может означать разный темп динамики, потому необходимо определить также, во сколько раз уровень одного периода более высок или более низок по отношению к уровню другого периода.

Темп роста позволяет ответить на вопрос: на сколько процентов он увеличился или уменьшился? Если оценивание в динамическом ряду проводится относительно предыдущего уровня, можно говорить о темпах роста, рассчитанных при переменной основе. При расчетах, проведенных относительно последующего уровня, говорим о показателях, рассчитанных на постоянную основу, которые еще называются показателями наглядности.

Абсолютный прирост может быть позитивным или негативным, и соответственно, темп прироста также может быть позитивным или негативным.

В определенных ситуациях, невзирая на снижение темпа прироста, мы можем отмечать одновременное увеличение абсолютного значения 1% прироста, который зависит от начального уровня.

Способы расчета указанных показателей приведены в табл.17.


Таблица 17. Динамика перинатальной смертности (на 1000 рожденных)

Год	Абсолютный уровень	Абсолютный прирост	Темп роста, %		Темп прироста %
			При сменной основе	При постоянной основе
n-5	14,3	----------	-----------	100,0	-------------
n-4	13,8	-0,5	96,5	96,5	-3,5
n-3	12,8	-1,0	92,7	89,5	-7,3
n-2	12,3	-0,5	96,1	86,0	-3,9
n-1	12,2	-0,1	99,2	85,3	-0,8
n	12,2	0,0	100,0	85,3	0,0

Наблюдения, которые проводят в течение длительного времени, не всегда дают возможность обнаружить четкую тенденцию в динамике определенного явления. В подобных ситуациях целесообразным является применение методов выравнивания динамичного ряда, которые разделяются на две основных группы:

1. 
   сглаживание - механическое выравнивание отдельных членов ряда с использованием фактических значений соседних уровней (приведение ряда к одной основе, метод усреднения по левой и правой половине, метод увеличения интервалов, метод групповой, и скользящей средней);
   

1. 
   выравнивание с использованием кривой, проведенной между конкретными уровнями таким образом, чтобы она отображала тенденцию, характерную для ряда, и одновременно освободила его от незначительных колебаний (выравнивание по методу наименьших квадратов).
   

Приведение ряда к одной основе осуществляется путем вычисления показателей наглядности. Динамика в данном случае выражается достаточно четко.

Методы выравнивания динамических рядов: метод усреднения по левой и правой половине; метод увеличения интервалов; метод переменной средней; метод наименьших квадратов.