Книга БИОСТАТИСТИКА (Автосохраненный). Биостатистика
 Скачать 1.08 Mb. Скачать 1.08 Mb.
|
|
Метод усреднения по левой и правой половине (графический метод). Ряд распределяется на две части. Для каждой его половины находят среднее арифме тическое значение и проводят через полученные точки линию на графике. Метод увеличения интервалов. Если рассматривать определенные медико-социальные показатели за ряд лет, то в результате влияния разнообразных факторов можно отметить сни жение и повышение отдельных уровней ряда. Это мешает выявить основную тенденцию развития определенного явления. Поэтому для наглядного представления динамики используют метод, который базируется на увеличении периодов времени, к которым принадлежат уровни ряда. Например, ежесуточное число вызовов скорой помощи можно заменить соответствующим показателем, определенным за неделю. Метод скользящей средней. Часто данный метод используют при проведении характеристики сезонных колебаний. Особенность его заключается в том, что проводится замена отдельных уровней ряда средними значениями, рассчитанными из настоящего и соседних уровней. Рассчитывают средний уровень для определенного числа (чаще трех) первых по порядку уровней ряда, потом средний уровень для ана логичного числа уровней, но начиная со второго, дальше с третьего и так далее. Таким образом, методика скользящей средней позволяет обнаружить тенденцию, которая была замаскирована случайными колебаниями показателей Метод наименьших квадратов. Данная методика базируется на математическом законе — через ряд эмпирических точек можно провести только одну прямую черту, которая отвечает требованию: сумма квадратов отклонений фактических данных от выровненных будет наименьшей. По данному мето ду определяется линия, которая больше всего подходит для эмпирических данных и дает характеристику направленности исследуемого явления. Ею является парабола соответствующего порядка. Для примера рассмотрим выравнивание по прямой (парабола первого порядка). Уравнение прямой линии имеет вид: y, = a0 + a1x x – порядковый номер года или другого периода времени; y, - теоретические уровни; a0 – начальный уровень; a1 – начальная скорость ряда. Расчет по прямой по методу наименьших квад ратов упрощается соответствующим подбором способа расчёта времени (х) таким образом, чтобы х = 0. При таких условиях расчет параметров a0 и a1 проводится по фор мулам: 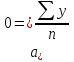 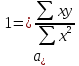 a0 и a1 – постоянные параметры для подстановки их в уравнение; n – число членов ряда; x – обозначение единицы времени. Методика выравнивания приведена на примере динамики смертности младенцев в Украине за 1992—1998 гг. (таблица. 18). Таблица 18. Динамика младенческой смертности в Украине
1. Принимаем средний период времени за начало отсчета (в 1993 г.). Время приведено в условных единицах от середины отсчета (ряд х),S x = 0. 2. Определяем постоянную величину уравнения (a0): 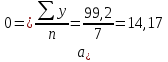
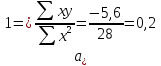
Yx = a0+a1x Y1 = 14,17 + (-0,2) х (-3) = 14,77 Y2 = 14,17 + (-0,2) х (-2) = 14,57 ……………………………. Y7 = 14,17 + (-0,2) х 3 = 13,57 Фактические показатели смертности младенцев и выровненный динамический ряд по методу наименьших квадратов представлены на рис. 16. 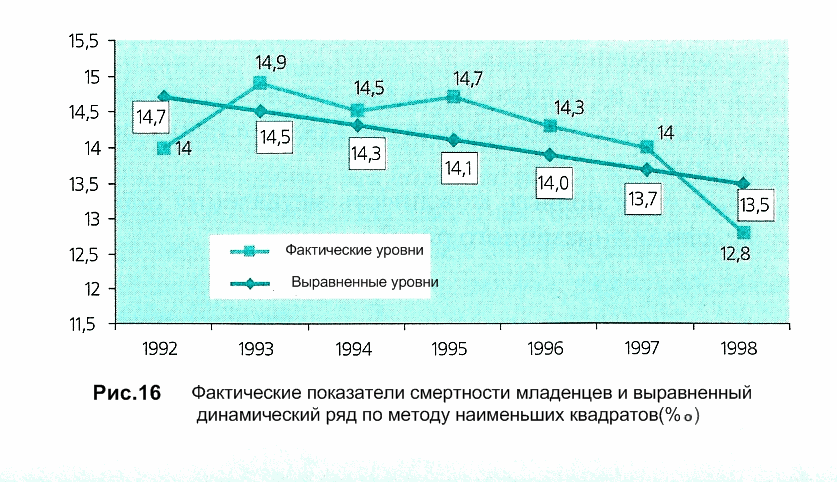 Анализ динамики медико-социальных явлений, обозначение и характеристика главных тенденций их развития формируют основу для последующего прогнозирования, определения будущих размеров уровня явления. Особенно ак туальными вопросы прогнозирования становятся в условиях пе реходу на новую методологию учета определенных явлений, в период реформирования системы здравоохранения. Прог нозирование предусматривает сохранение основных зако номерностей в будущем, таким образом, оно ба зируется на экстраполяции.
Теоретической основой распространения тенденции на будущее является инерционность основных социальных, медицинских, экономических процессов. Чем короче является срок экстра поляции, тем надежнее и более точным является прогноз. В зависимости от того, какие принципы и восходящие данные положены в осно ву прогноза, выделяют такие элементарные методы экстра поляции:
Динамика ряда включает три компонента:
Изучая динамические ряды, исследователи с древних времен пытаются разделить эти компоненты и обнаружить глав ным образом основную закономерность развития явлений в отдельные промежутки времени, то есть обнаружить общую тенденцию в изменении уровней ряда, которое освобождено от влияния отдельных факторов. Именно с этой целью ряды динамики обрабатывают с помощью известных методов. Вопросы для контроля:
3.5. Характеристика и анализ статистической совокупности В подразделе|подразделении| изложено практическое|практичное| значение и виды средних величин, методика их расчета, описанные ха рактеристики| и параметры вариационного ряда. Вопрос для изучения:
Цель: ознакомить с элементами и характеристиками вариационных рядов, научить рассчитывать средние вели чины| и другие параметры вариационного ряда, проанализировать| практическое|практичное| использование|употребление| средних величин.
Сбор, регистрация и благоустройство данных, в процессе любого исследования завершается формированием статистической совокупности (Statistical aggregate), которую можно определить как совокупность объектов или явлений одного вида, объединенных по определенному признаку. Например, больные с определенным диагнозом, определенным методом лечения и так далее. При этом для всех явлений, которые изучаются в медицине, характерна изменчивость, вариабельность. Каждый человек имеет количественную оценку определенного набора физиологических и клинических параметров, которые являются индивидуальными. Но в группе людей любой клинический параметр может изменяться и приобретать значения в определенном диапазоне.
Прежде чем|перед тем как| давать характеристику вариабельности| совокупности|, что имеет разные|различные| значения признаков в отдельных ее единицах|, необходимо иметь единственную|единую| типичную|типовую| для совокупности ве личину| (показатель), что позволяет дать ее обобщённую характеристику. Для этого применяются средние величины, которые|какие| рассчитываются только по количественным признакам|, то есть определение средней для атрибутивных признаков невозможно.
В практике здравоохранения|здравоохранительный| средние величины используются достаточно широко: • для характеристики организации работы учреждений охраны здоровья (средняя занятость койки, средний срок пребывания в стационаре и др.);
• для оценивания данных медико-социальных и санитарно-гигиенических исследований (среднее число лабораторных исследований, средние нормы питательного рациона, средний уровень радиационного загрязнения, но|да| др.).
Свойством средней величины является ее обобщённая характеристика. Средняя величина рассчитывается путем сопоставления абсолютных или относительных величин. При этом качественно однородная совокупность и достаточное число наблюдений является основными требованиями для расчета средних величин. Смешивание совокупности, которая определяется разными качественными признаками, приводит к расчету нетипичных средних величин, которые не могут быть основой научного анализа. Как избежать качественной неоднородности, решается во время планирования исследования и во время группирования первичного материала на основе качественного анализа исследуемых явлений. Например, нельзя изучать клинические параметры больных вообще, без деления их за нозологическими формами, возрастом и так далее Необходимо число наблюдений определяется за соответствующими методиками в зависимости от характера данных и дизайна исследования. Распространен шаблонный подход отбора не меньше N (ЗО, 50, 100) пациентов является априорным, что недопустимо в клинических исследованиях. Средняя величина имеет двойственный характер: с одной стороны она характеризует совокупность в целом, а из|с| второго — она является основой|основанием| для оценки отдельных единиц совокупности|, их разнообразия и изменчивости|переменчивости|. 1. По форме расчета можно выделить: а) среднюю арифметическую величину; б) среднюю гармоничную величину; в) среднюю геометрическую величину; г) среднюю квадратичную, кубическую, и другие величины. 2. За охватыванием|охватом| совокупности выделяются: а) групповая средняя величина; б) общая средняя величина. Рассмотрим подробнее отдельные виды средних вели чин|. Средняя арифметическая является самым распространенным видом средних величин. Она отображается|обозначается| как X. Однако, часто средняя арифметическая отражается|обозначается| буквой М (лат. Media|). За характером данных она может быть простою или взвешенной|. Средняя арифметическая простая определяется как сумма вариант вариационного ряда, разделенная на их число. При этом вариационный ряд — это совокупность числовых значений признаков (вариант), которые могут быть не систематизированы за своим абсолютным значением (неранговый ряд), систематизированные в порядке роста или уменьшения - (ранговый ряд).
Вариационный ряд может быть простым, где каждая варианта представлена отдельно, потому частота каждой из них равняется единице. Например, распределение больных по частоте пульса: 68, 69, 75, 70, 65, 68, 70, 75, 74, 72, 72, 68. Данный ряд также неранговый, потому что варианты не систематизированы. Систематизировав варианты в порядке увеличения или уменьшения их числового значения, данный ряд можно превратить в ранговый: 65, 68, 68, 68, 69, 70, 70, 72, 72, 74, 75, 75. Если варианты сгруппировать за их абсолютным значением|, то можно получить сгруппированный вариационный ряд, где каждая варианта имеет свою частоту. Например:
Приведенный сгруппированный ряд является неинтервальным , потому что группирование|группировка| проведено за абсолютным значением каждой варианты. Вариационные ряды, где значение вариант представлен в виде интервалов, называются интервальными. В виде| интервального ряда часто представляют признаки со значительным количеством вариант. При этом значение каждой варианты поданы в виде интервала (см. ниже).
В приведенной|наведенной| таблице интервалы являются закрытыми — каждый из них имеет верхний и нижний предел|границу|. В практике попадаются открыты интервалы (возраст|век| 60 лет и старше, рост до 120 см но|да| др.). В процессе анализа ширину открытого интервала|, конечно, принимают ровной|равной| ширине смежного с ним интервала. Сгруппированный интервальный вариационный ряд можно получить путем объединения вариант в группы. При этом необходимо помнить, что: а)размер вариационных групп должен зависеть от природы| явления; б|б|) имеет смысл определять одинаковые интервалы; в) границы вариационных групп не должны повторяться. Все вариационные ряды за качественной характеристикой распределяются на дискретные, в которых|каких| варианты могут быть представлены только целыми числами или полученные в результате подсчетов|вычисления| (распределение|деление| за частотою пульсу|, числом кроватных|постель| дней, посещений) и инкретные (непрерывные|), где варианты могут быть представлены как целыми, так и дробными, числами, или является результатом измерений (приведена|наведенный| таблица). Клинические параметры являются по большей части примером|прикладом| инкретных| вариант. В процессе проведения исследования вопроса о чис ло| вариационных групп решают|разрешают| учитывая характер ма териала| и численность совокупности. Характерные особенности по распределению|делению| не окажутся|проявляются|, если при незначительном числе единиц наблюдения взять значительное число групп, или если число групп является недостаточным. Одним из вариантов автоматического группирования|группировки| есть использование|употребление| формулы Стерджеса для определения оптимального числа групп: n=1+3,322 х lgN n – число групп; N – число единиц наблюдения Использование|употребление| данной формулы целесообразное при большом|великом| числе единиц наблюдение. Другим вариантом, более гибким с практической точки зрения, является метод определения амплитуды ряда (разница между максимальным и минимальным значением варианта). Для решения вопроса о числе групп необходимо подать статистическую совокупность в виде рангового ряда, то есть разместить ее единицы в определенном порядке. При численности совокупности менее 100 единиц не целесообразно планировать больше 10 групп. Этапы составления|сдает| интервального вариационного ряда:
Расчет средних величин базируется на значениях вариант. Если вариант представлен в виде интервала за величину в каждом из них принимают центральный вариант, то есть середину|средину| интервала. Для дискретного ря да| центральный вариант определяется как полусумма| одного интервала. Для инкрементного ряда (предыдущий|предварительный| пример|приклад|) ею является полусумма начальных|первоначальных| значений двух соседних интервалов|: (125,0+127,0)/2=126 см.
Взвешенная средняя арифметическая определяется как сумма произведений вариант на соответствующие частоты, разделенная на общее число наблюдений. Частоты отражаются|обозначаются| бук вою| f (frequency|) и указывают, сколько раз встречается каждая варианта в вариационном ряду. Если варианты обозначить X, частоты f, общее чис ло наблюдений, — буквой N, арифметическую сумму сим волом Σ, то формула средней арифметической будет иметь вид: 1) для простого ряда (простая средняя арифметическая): 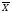 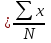 2)для сгруппированного ряда (взвешенная средняя арифметическая): 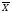 = =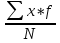
Наряду со средней арифметической, для статистич еского анализа применяются, хотя и реже, другие виды с редних: средняя гармоничная и средняя геометрическая. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||