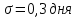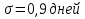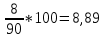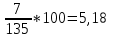Книга БИОСТАТИСТИКА (Автосохраненный). Биостатистика
 Скачать 1.08 Mb. Скачать 1.08 Mb.
|
|
Средняя гармоничная определяется в тех случаях, когда известны данные числителя при отсутствии данных о знаменателе. Xгарм= 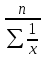 Например, необходимо определить среднее время, тратящее на прием одного больного, когда известно, что 5 врачей вели прием в течение|на протяжении| 8 часов. Каждый из них тратил в среднем на прием одного больного, соответственно 20; 16; 20; 15; 24 минуты. Средняя арифметическая (М=17,75) в данном случае не даст точную оценку результату, поскольку каждый из врачей принял различное|различную| ' количество пациентов.
Среднюю гармоничную целесообразно использовать также при оценивании выживания больных, средней длительности жизни, некоторых|некоих| экономических|экономичных| показателей. Средняя геометрическая определяется для тех параметров, изменения значений которых проходят в геометрической прогрессии (изменение численности населения в период между переписями, результаты титрования вакцин, прирост массы тела новорожденных в течение отдельных месяцев жизни, но др.). Формула для расчета простой средней геометрической следующая: Mгеом= 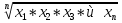 или lgMгеом= 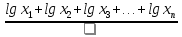 Логарифм средней геометрической равняется сумме логарифмов всех членов ряда, разделенных на их число. Лога рифм полученного результата есть средняя геометрическая.
Иногда в здравоохранении|здравоохранительный| для характеристики показателей используют среднюю реверсивную|. Дана вели чина| рассчитывается из|с| вариант, которые|какие| имеют среднюю| прогрессивную длительности лечения больных в стационарах, и будет рассчитываться из значений, какие более малые среднего уровня длительности госпитализации для всей исследуемой совокупности. Такая средняя может служить базой для определения оптимального уровня определенного показателя|. К|до| средним величинам, которые имеют относительный характер относятся медиана и мода. Что такое медиан мода? Медиана (Me|) — это срединная, центральная варианта, который делит вариационный ряд на две равных части. Например, когда число наблюдений составляет 29, медианой будет 15-я| за счетом|счет-фактурой|, потому что по оба бо ки| от нее стоит по 14 наблюдений. В ряду с парным|четным| числом наблюдений центральное положение имеют две величины. Если числовые значения этих две величин разные|различные|, то за медиану берется их полусумма|.
Рассматривая моду нельзя не рассмотреть понятие квартилей|, которые|какие| также применяются для характеристики совокупности. Квартили — это значения, которые делят две половины совокупность (разделенные медианой) еще раз пополам (от слова кварта — четверть). Выделяют верхний квартиль|, который|какой| часто помечают символом 75 % (значит|означает|, что 75 % вариант меньше верхнего квартиль|). Нижний квартиль 25 % (25 % вариант меньше нижнего квартиль|). Таким чи ном|, три точки — нижний квартиль|, медиана и верхний квартиль — делят выборку на 4 равных части.
Мода (Мо) — величина, которая чаще всего встречается, или чаще всего повторяется. Отвечает на графическом изображении максимальной ординате, то есть наивысшему значению графической кривой. Таким образом, при приближенном нахождении моды в простом (несгруппированному) ряду она определяется как варианта с наибольшим количеством частот (например: 2, 6, 6, 8, 9, 9, 9, 10 — мода = 9). При этом ряд может иметь бимодальный (два значения случаются с одинаковой частотой), полимодальный характер. Отличие медианы и моды от средней арифметич еской| заключается в том, что эти величины определяются достаточно легко и не зависят от крайних вариант или от степени рассеивания ряда. Средняя арифметическая часто имеет ограниченное значение потому, что она не отображает размеры колебания количественных вариант ряда (вариабельность ряду).
Важной характеристикой ряда является оценка разнообразности (изменчивость|переменчивость|, вариабельности|) вариант исследуемой совокупности. Вариацией является изменчивость|переменчивость| только тех признаков, на которые|какие| влияют внешние|наружные| факторы, при чини| ли. Явления, которые изменяются в силу своей природы, нельзя характеризовать как вариацию, например изменение|смена| роста ребенка от роду к|до| совершеннолетию. Нас в первую очередь |первоочеринтересует именно случайная вариация, поскольку это понятие является основой|основанием| формирования и оценка нормы и патологии в медицине. Одной из характеристик разнообразия вариант ряда является его амплитуда — разница между крайними значениями. Однако, амплитуда не учитывает характер распределения вариант, потому она имеет ограниченное использование в медицине. Например, два вариационных ряды с разной амплитудой могут иметь одинаковое значение средней арифметической. Для анализа вариации признаков исследуемой совокупности необходимо использовать показатели, которые учитывают значение всех единиц наблюдения данной совокупности. Таким показателем является среднее квадратичное отклонение (стандартное отклонение — standard deviation), что позна чається символом σ (сигма). Среднее квадратичное отклонение учитывает степень разнообразия всех вариант совокупности относительно средней арифметической и определяется по формуле: 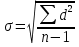 • для простого вариационного ряда. • для простого вариационного ряда.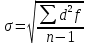 • для сгруппированного вариационного ряда. • для сгруппированного вариационного ряда.где n — число наблюдений в исследуемой совокуп ности (при достаточно большом числе наблюдений — n > 30 — в формуле вместо n —1 можно использовать n); f— час тота вариант; d = х - X — отклонение каждой варианты от средней арифметической; х — значение варианты.
Методику расчета среднего квадратичного отклонения рассмотрим на примере оценки средней длительности лечения больных пневмонией в стационаре (см. таблицу.). Величина амплитуды для вариационного ряда с нормальным распределением вариант приблизительно равняется шесть сигм (5), потому чем выше является значение среднего квадратичного отклонения, тем выше является степень разнообразия признаков совокупности и менее типичной средней.
Правило нормального распределения вариант в вариационном ряду можно определить как правило трёх сигм (Х± 3σ) — относительно средней арифметической практически все варианты совокупность находится в диапазоне ± 3σ. Схематично это можно отобразить так: Согласно теории статистики, которая имеет как арифметическое, так и геометрическое, доведение (по площади фигур) в пределах X ± 1σ будут находиться не менее 68,37 % всех вариант совокупности. За пределами данного интервала может быть до 31,63 % всех наблюдений. В пределах X ± 2σ будут расположены около 95,45 % всех вариант. Практически весь вариационный ряд — 99,7 % вариант будет находиться в диапазоне X ± 3σ. Отдельные варианты — до 0,3 % исследуемой совокупности могут не отвечать общему ха рактеру распределению и выпадать из него в результате слишком низкого или высокого уровня («выскакивающие» варианты). 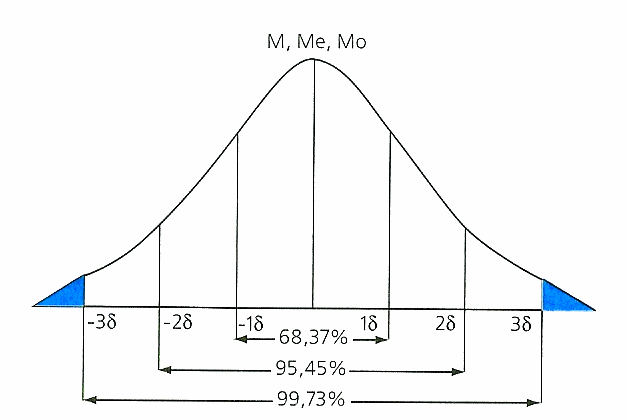
Для вышеуказанных условий значения средней арифме тической моды и медианы будут одинаковыми. Среднее квадратичное отклонение (как мера вариации) поданная в квадрате называется дисперсией. В сущности дис персия — это средняя величина квадратов отклонений вариант от средней арифметической. Данный показатель также используется в медицине и биологии для харак теристики однородности исследуемой совокупности. При малых значениях σ средняя арифметическая достаточно полно характеризует совокупность (является типичной), тогда как большое зна чение σ свидетельствует о неоднородности вариационного ряда (нетипичность средней). В медицине при разработке критериев нормы часто принимается диапазон X ± 1σ (реже X ± 1,5 σ). С помощью σ можно оценить «выскакивающие» (нетипичные) варианты: 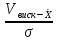 При условии, что результат выше 3 — данную варианту целесообразно исключить из последующего анализа.
На практике иногда возникает потребность сравнить степень однородности (разнообразие) разных параметров сово купности. Среднее квадратичное отклонение — именуемая величина, потому непосредственно сравнивать средние квадратичные отклонения вариационных рядов с разными единицами измерения (длина в сантиметрах, вес в килограммах) нельзя.
Для обеспечения сопоставления необходимо определить для каждого ряда коэффициент вариации (С) — отношение среднего квадратичного отклонения (сигмы) к средней арифметической в процентах. Данный показатель является относительной мерой вариабельности, что выражается в процентах, а не именуемых числах: 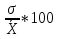
Чем выше коэффициент вариации, тем большая вариабельности данного признака. Критерием в данном случае является такая оценка: С < 10 % — низкий уровень вариабельности; С = 10 - 25 % — средний уровень вариабельности; С > 25 % — высокий уровень вариабельности свидетельствует о невозможности использования данной совокупности для анализа, необходимость расчета по групповых средних или исключения отдельных «выскакивающих» вариант. 1.Каким требованиям|востребованию| должен отвечать материал исследования при определении средних величин?
|

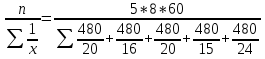 =
=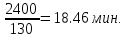
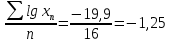 Mгеом = 0,056
Mгеом = 0,056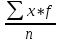 =816/48=17 дней
=816/48=17 дней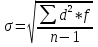 =
=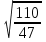 =
=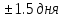
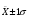 в большинстве случаев определяет их средний уровень;
в большинстве случаев определяет их средний уровень;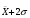 - выше или ниже средних;
- выше или ниже средних;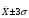 - очень высокие или очень низкие уровни показателей
- очень высокие или очень низкие уровни показателей