Книга БИОСТАТИСТИКА (Автосохраненный). Биостатистика
 Скачать 1.08 Mb. Скачать 1.08 Mb.
|
|
Таблица 22. Результаты лечения больных по отдельным методикам
Таблица 23.
Таблица 24.
Таблица 25.
n1= (S-| 1) (г-| 1), где S — число групп больных (для нашего примера |приклада| - три). г — число результативных групп (три). |Число степеней свободы n1= (3 - 1) (3 - 1) = 4.
Полученный результат превышает табличное значение X2 для n1 = 4 по всем уровням достоверности. Следовательно, мы можем сделать вывод о существенности (достоверность) разницы между показателями при разных методах лечения — «нулевая» гипотеза не подтвердилась. Вопросы для контроля:
3.8. Анализ взаимосвязи между параметрами статистической совокупности В подразделе описана сущность метода корреляционно регрессионного анализа, его практическое значение и мето дика расчета коэффициентов корреляции и регрессии. Вопросы для изучения: — Когда возникает необходимость применения корре ляционного анализа?
Цель: обосновать необходимость использования ме тода корреляционно регрессионного анализа; научить рассчитывать ρ и анализировать коэффициенты корреляции и регрессии. Все изменения, которые происходят в природе, являются взаимосвязанными и взаимообусловленными. Изменчивость определенного признака как следствие изменчивости других параметров, в свою очередь, обуславливают изменчивость других признаков. Однако, указанная зависимость в отдельных ситуациях проявляется по-разному. Функциональная связь часто присутствует при изучении химических и физических явлений, в математике, геометрии.
В медико-биологических исследованиях зависимость между отдельными параметрами не является функциональной связью. При изменении одного признака невозможно абсолютно точно спрогнозировать величину, на которую изменяются другие. Примером такой корреляционной связи является зависимость веса и роста детей, тяжести патологии и сроков лечения, концентрации вредных веществ в рабочей зоне и уровень заболеваемости работников.
Определение характера связи между определенными параметрами проводят путем расчета коэффициента корреляции, который в зависимости от его характера и формы представления данных может быть рассчитан разными методами. Таблица 26.
Коэффициент парной корреляции отображает характер связи 2 признаков. Он может быть рассчитан при сопоставлении двух рядов в виде рангового коэффициента корреляции (ρ) и линейного коэффициента корреляции (r).
Корреляционная зависимость различается по направлению, силе и форме связи (таблица 26). По направлению корреляционная связь может быть положительной ("прямой") и отрицательной ("обратной"). Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции. Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции. Максимальное возможное абсолютное значение коэффициента корреляции r = 1,00; минимальное r = 0,00.
Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы: 1) Определить каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию). 2) Определить разности рангов каждой пары сопоставляемых значений. 3) Возвести в квадрат каждую разность и суммировать полученные результаты. 4) Вычислить коэффициент корреляции рангов по формуле: ρ =1- 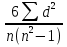 где
Методика расчета на примере характеристики взаимосвязи стажа работы работников угольной промышленности и частотой заболеваний на бронхит в них.
При большом числе наблюдений ( n> 100) средняя погрешность рангового коэффициента корреляции может быть определена по формуле: mp= 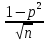 Оценка достоверности коэффициента корреляции про водиться по тем же принципами, что используются для других показателей с учетом числа наблюдений (числа степеней свободы вариационных рядов n` = n – 2). Один из методов расчета коэффициента линейной корреляции был предложен К.Пирсоном. Формула для подсчета коэффициента корреляции Пирсона такова: r = 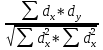 X и Y – варианты сравниваемых вариационных рядов; dx и dy – отклонение каждой варианты от своей средней арифметческой Таблица 28. Зависимость между составом железа в крови и уровнем гемоглобина в крови.
Расчет линейного коэффициента корреляции:
Достоверность полученного результата определим соотношением t = r / mr, где mr при малом числе наблюдений (n < 30) равняется: mr= 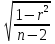 При большом числе наблюдений (n > 100) формула для расчета средней погрешности коэффициента корре ляции может иметь вид: m= 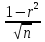 Прямолинейная корреляционная связь между парамет рами характеризуется тем, что каждому из одинаковых измерений одного показателя отвечает определено среднее зна чение другого показателя. Данную зависимость можно описа ть коэффициентом регрессии. Рассчитывается коэффициент рег рессии по формуле: Rx/y=rxy* 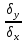 Где: Rx/y - коэффициент регрессии от Х до У; rxy - коэффициент корреляции; 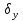 и и 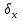 средние квадратические отклонения рядов Х и У. средние квадратические отклонения рядов Х и У.
Выше приведенные методики расчета парных ко эффициентов корреляции являются основой и только первым этапом многофакторного корреляционной анализа. Парные ко эффициенты показывают характер связи (общего, «неочищенного») между исследуемыми параметрами без учёта влияния других факторов. Оценивание «чистой» взаимосвязи в многофакторных моделях определяется на основе парциальных коэффициентов корреляции, основой для расчета которых являются парные и множественные коэффициенты. В практике медицинских исследований достаточно часто возни кает вопрос об определении влияния нескольких разных факторов на определенное явление, например, на частоту осложнений при родах влияет возраст женщины, наличие аку шерской и экстрагенитальной патологии, качество предоставления медицинской помощи и др. В таких случаях для выявления комбинированного влияния нескольких факторов на размер исследуемого явления пользуются методом множественной корреляции. Использование этого метода про водиться в несколько этапов. Математический аппарат данно го анализа является достаточно сложным и выходит за пределы програ ммы подготовки врачей. В настоящее время существует много специализирова нных программ статистического анализа, которые позволяют рассчитать множественный коэффициент корреляции для определенной совокупности показателей. Важным является оценка резуль тата: в случае, когда сумма парциальных коэффициентов ко рреляции меньше величины множественного коэффициента ко рреляции, мы можем говорить о потенцируемом действии исследуемых параметров относительно результативного приз нака. Иначе (что, по нашему опыту, случается чаще) мы можем отмечать параллельное влияние факторов с невыраженным взаимным потенцируемым эффектом с условия, когда сумма парциальных коэффициентов значительно превышает значение множественного коэффициента корреляции. Следовательно, множественный коэффициент корреляции отображает связь одновременно комплекса факторов с исследуемым ре зультативным фактором (клиническими показателями и др.). Вопросы для контроля:
3.9. Методы многофакторного анализа Одним из важных моментов при изучении состояния здоровья населения и деятельности системы охраны здоровья является анализ действия многочисленных факторов, которые формируют здоровье людей, влияют на рост заболеваемости, приводят к инвалидности или смерти пациентов. Тем более при разработке профилактических способов улучшения состояния здоровья населения, состояния окружающей среды, деятельности медицинских учреждений растет значимость оценивания факторов. Биостатистика владеет большим количеством возможностей для этого, необходимо только научиться правильно подбирать методы статистического анализа, которые являются наиболее адекватными для данного конкретного исследования. Благодаря использованию методов корреляционно-регрессивного, факторного, дисперсионного, кластерного анализа медицинская статистика превратится из описательной в аналитическую. Одним из распространенных методов анализа является корреляционный анализ(см.выше). Коэффициент линейной корреляции существует 3 типов:
Парный коэффициент корреляции дает характеристику обобщенной, «неочищенной» связи между параметрами. При этом возможно влияние других факторов, которые не учитываются, поэтому самостоятельная ценность парного коэффициента не высока. Поэтому чаще используют парциальные коэффициенты (которые можно рассчитать при наличии парных коэффициентов корреляции). Они отражают связь между факторами и уровнем здоровья в чистом виде, исключая влияние других факторов. Множественный коэффициент корреляции отражает одновременно связь изучаемых факторов с результативным признаком. Степень влияния факторов характеризуется т.н. коэффициентом детерминации-квадраты парциальных коэффициентов, перемноженные на 100 (в процентах). . Коэффициент детерминации отображает искомый вес влияния на здоровье данного фактора среди других. Регрессионный анализ чаще проводится вместе с корреляционным, поэтому его и называют корреляционно-регрессионным. Главная задача регрессионного анализа -составить уравнение регрессии, которое описывает «поведение», например, профессионального заболевания при изменении интенсивности влияния включенных в исследование факторов (пола, возраста, профессии, стажа работы, условий работы). Дисперсионный анализ. Основной целью дисперсионного анализа является исследование значимости различия между средними. Может показаться странным, что процедура сравнения средних называется дисперсионным анализом. В действительности, это связано с тем, что при исследовании статистической значимости различия между средними двух (или нескольких) групп, мы на самом деле сравниваем (т.е. анализируем) выборочные дисперсии. Фундаментальная концепция дисперсионного анализа предложена Фишером в 1920 году. Возможно, более естественным был бы термин анализ суммы квадратов или анализ вариации, но в силу традиции употребляется термин дисперсионный анализ. Чтобы проиллюстрировать логику дисперсионного анализа, рассмотрим простой план эксперимента, включающий одну независимую переменную (или фактор А) и, скажем, 3 группы испытуемых. Целью такого плана обычно является выяснение того, изменяется ли зависимая переменная как функция фактора А.. Дисперсионный анализ позволяет нам проверить нулевую гипотезу об отсутствии действительных эффектов данного фактора - и тогда различия в показателях вызваны исключительно случайной изменчивостью. Предполагая, что нулевая гипотеза верна, можно получить две разные оценки дисперсии генеральной совокупности. Одна из этих оценок вычисляется на основе изменчивости групповых средних, а другая - на основе дисперсии показателей внутри каждой включенной в план группы. Если нулевая гипотеза и в самом деле верна, то обе оценки являются, по существу, оценками одной и той же генеральной дисперсии. Как следствие, эти оценки будут иметь одинаковую величину, за исключением случайной изменчивости, а их отношение будет иметь известное теоретическое. Если нулевая гипотезе не верна, то наши выборочные оценки не являются оценками дисперсии одной и той же генеральной совокупности, т. к. на первую будут влиять любые реальные эффекты фактора, а на вторую – нет. Дискриминантный анализ используется для принятия решения о том, какие переменные различают (дискриминируют) две или более возникающие совокупности (группы). Предположим, что вы измеряете рост в случайной выборке из 50 мужчин и 50 женщин. Женщины в среднем не так высоки, как мужчины, и эта разница должна найти отражение для каждой группы средних (для переменной Рост). Поэтому переменная Рост позволяет вам провести дискриминацию между мужчинами и женщинами. Термин кластерный анализ (впервые ввел Tryon, 1939) в действительности включает в себя набор различных алгоритмов классификации. Общий вопрос, задаваемый исследователями во многих областях, состоит в том, как организовать наблюдаемые данные в наглядные структуры, т.е. развернуть таксономии. Например, биологи ставят цель разбить животных на различные виды, чтобы содержательно описать различия между ними. В соответствии с современной системой, принятой в биологии, человек принадлежит к приматам, млекопитающим, амниотам, позвоночным и животным. Заметьте, что в этой классификации, чем выше уровень агрегации, тем меньше сходства между членами в соответствующем классе.
Таким образом, все указанные методы многофакторного анализа расширяют возможности исследователя относительно статистического анализа полученных результатов, необходимо только научиться их правильно подбирать и смело использовать. Вопросы для контроля:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

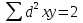
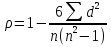 =1-6*2/5*(25-1)=
=1-6*2/5*(25-1)=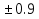
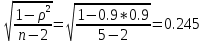
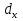
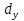
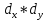
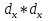
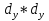
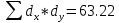
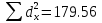
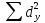 =34.89
=34.89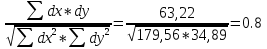
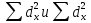
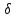
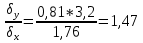 (кг)
(кг)