Моделирование. 090402 Имитационное моделирование экономических процессов. Цель и метод планирования экспериментов
 Скачать 440.5 Kb.
|
2. Этапы планирования имитационных экспериментовЭкспериментом называют научно поставленный опыт для целенаправленного изучения некоторого явления в точно учтенных условиях, когда можно проследить ход изменения явления. Целью экспериментальных исследований является получение новой информации при изучении различных сложных систем. По возможности исследователя влиять на независимые факторы эксперименты подразделяют на пассивные и активные. Пассивный эксперимент заключается в анализе результатов наблюдений, которые зависят от многих одновременно действующих факторов. Активный эксперимент позволяет исследователю определенным образом планировать эксперимент, чтобы упростить процедуру оценки влияния каждого из факторов, а также при необходимости воссоздавать эксперимент многократно. Традиционный способ изучения зависимости исходной величины от многих независимых факторов заключается в её исследовании отдельно для каждого фактора при фиксированных значениях остальных факторов. Создаваемая при этом семья функций мало пригодна для практических целей и большей частью не содержит всей необходимой информации. Это и стало причиной необходимости планировать эксперименты. Такое планирование должно предусматривать привлечение к практике исследовательских работ средств, которые дают возможность повысить эффективность наблюдений, получить наглядную интерпретацию результатов и наилучшим образом оценить случайные и систематические ошибки опытов. Эти вопросы рассматриваются в научной дисциплине ― теории планирования экспериментов, начало которой было положено в 1918 году работой Р. Фишера о разработке метода планирования экспериментов ― дисперсионного анализа. Большое значение для развития теории планирования экспериментов имела опубликованная в Англии 1951 года работа Бокса и Уилсона о проблемах планирования экспериментов многофакторных процессов для поиска оптимальных решений способом одновременного варьирования по заданным правилам всех факторов исследуемого процесса. Планирование эксперимента ― это разработка такого плана эксперимента, который дает возможность с минимальным количеством опытов (а значит, затрат материальных, трудовых и временных ресурсов) сделать статистически значимые выводы или найти оптимальные решения относительно функционирования системы. Уменьшение числа попыток не должно существенно сказаться на качестве полученной информации. В экономических исследованиях теория планирования экспериментов имеет довольно ограниченное распространение, прежде всего из-за сложности или невозможности постановки активных экспериментов в реальных условиях. Тем не менее, разработка методов машинной имитации дала возможность вести активные машинные эксперименты с моделями экономических систем. Во время выполнения натурных или машинных экспериментов могут решаться две основные проблемы: исследование систем ― выявление закономерностей развития системы и установление количественных соотношений между переменными величинами и параметрами, которые описывают функционирование системы; оптимизация систем ― установление значений факторов, которые обеспечивают оптимальный режим функционирования системы. План эксперимента размещается в факторном пространстве. Факторное пространство ― множество значений внешних и внутренних параметров модели (факторов)  , которые предположительно влияют на результаты экспериментов и значения которых может контролировать исследователь. Факторное пространство можно представить как сетку точек, каждая из которых отвечает одному опыту. Значения факторов называют уровнями.Пусть y ― эндогенная случайная величина, а – контролируемые во время опытов факторы. Тогда изучаемый процесс описывается так: (1) Функцию  называют функцией (реакцией, поверхностью) отклика.Задача исследования системы заключается в установлении зависимости (1) или выявлении величины влияния разных факторов или их комбинаций на функцию отклика. При оптимизации систем необходимо определить такие уровни факторов, в которых функция отклика приобретает экстремальные значения. В таком случае эндогенную величину y называют параметром оптимизации, а функцию отклика ― целевой. Поверхность отклика для функции одной переменной вырождена в линию. Для двух факторов поверхность отклика представляет собой поверхность в трехмерном пространстве. К факторам при планировании экспериментов выдвигаются требования относительно: измеримости и управляемости. В отличие от натурных экспериментов при имитационном моделировании любой фактор может быть управляемым; независимости, т.е. установление некоторого уровня одного фактора не должно зависеть от взятых значений других факторов; совместимости – любые комбинации уровней факторов должны быть осуществимы. Следует установить границы областей определения факторов, их основные уровни и интервалы варьирования. При выборе количества уровней нужно выполнять два противоречивых требования: уровни фактора должны перекрывать весь возможный диапазон его изменения; общее количество уровней всех факторов не должно приводить к завышенному объему моделирования. Выбор основных уровней (начальной точки факторного пространства) и интервалов варьирования основывается на предварительных знаниях относительно исследуемого процесса. Делают этот выбор, исходя из необходимости уменьшения числа опытов для решения поставленной задачи. Например, для поиска оптимального значения функции отклика в качестве начальной точки может быть выбрана точка факторного пространства, которая на основании некоторых соображений должна лежать вблизи области экстремума. Итак, для каждого і-го фактора определяются:  – основной уровень і-го фактора; – верхний уровень і-го фактора; – нижний уровень і-го фактора; – интервал варьирования.Во время проведения экспериментов используются кодированные значения уровней факторов. Кодирование выполняют по формуле:   . (2)После кодирования верхний уровень примет значение +1, нижний ― значение –1, основной уровень будет равен нулю. Количество всех точек факторного пространства при двухуровневой системе смены факторов, для которых необходимо экспериментально находить значение функции отклика, равняется 2n, где n – число факторов. Сначала функцию отклика (1) берут в виде линейной зависимости:  , (3)где  ― коэффициенты при факторах.После проверки ее на адекватность (в случае отрицательного результата), модель усложняют к неполному квадратичному полиному ― зависимости с учетом взаимодействия факторов: 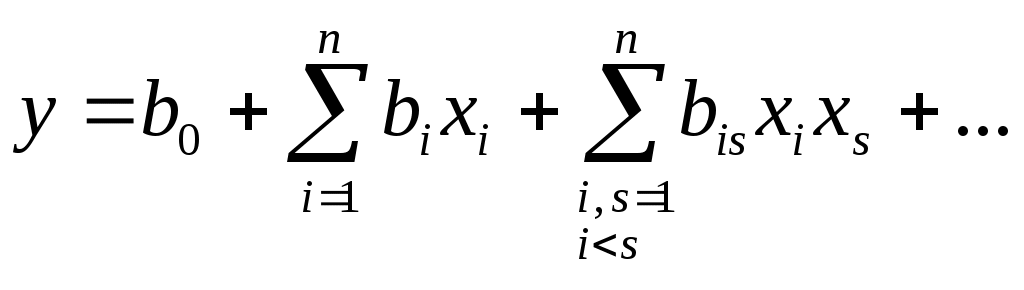 . (4)В случае неадекватности и этой модели, избирают полный полином второй степени: 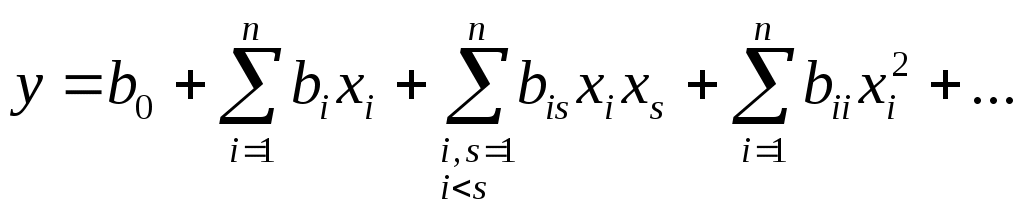 . (5)Обычно полинома второй степени достаточно, и лишь в редких случаях используется полином третьей степени. Если при проведении опытов возможны ошибки измерения эндогенной величины y, либо она является случайной величиной и оценивается с помощью математического ожидания, то y получают обработкой результатов установленного заранее числа дублирований эксперимента. Для определения коэффициентов уравнения регрессии экспериментально находят значение эндогенной величины y в N точках факторного пространства (при двухуровневой системе смены факторов  ). Попытки в каждой точке дублируются k раз. За расчетное значение функции отклика в некоторой точке факторного пространства берут среднее значение этого показателя. Число повторений опыта определяется статистическими методами в зависимости от принятой надежности и точности ожидаемых результатов (изложено в следующей теме).При планировании имитационного моделирования для повторений опыта можно использовать несколько разных генераторов случайных чисел. Для корректного выполнения регрессионного анализа необходимо, чтобы выполнялись рассмотренные ниже условия: 1. Результаты параллельных наблюдений  величины y в каждой из N точек факторного пространства представляют собой реализацию нормально распределенной случайной величины.2. Дисперсии реализаций  равны между собой, т.е. дисперсия величины y не зависит от того, с какой точкой факторного пространства проводят параллельные опыты; 3. Факторы ― независимые величины, измеренные с настолько малой погрешностью, которой можно пренебречь сравнительно с погрешностью определения величины у.В случае имитационного моделирования третье условие выполняется всегда, первое и второе должны проверяться с помощью специальных тестов. Существуют два варианта постановки задачи планирования имитационного эксперимента: из всех допустимых выбрать такой план, который позволил бы получить наиболее достоверное значение функции отклика при фиксированном количестве опытов; выбрать такой допустимый план, при котором статистическая оценка функции отклика может быть получена с нужной точностью при минимальном количестве опытов. Решение задачи планирования в первой постановке называют стратегическим планированием эксперимента, во второй ― тактическим планированием. Полным факторным экспериментом (планом) называется эксперимент, в котором реализуются все возможные объединения (комбинации) уровней факторов, т.е. N=un, где u – число уровней факторов. Чаще всего в экспериментах используется двухуровневая система изменения факторов. Число всех точек факторного пространства равняется 2n (базовая точка, в окрестности которой ищут аппроксимацию функции отклика, во внимание не принимается, поскольку в этой точке эксперимент не проводится). Полный факторный эксперимент удобно подавать в виде матриц планирования. Для трехфакторного эксперимента при кодированных значениях уровней факторов (5) такая матрица приведена в Таблице 1. Таблица 1 – Матрица планирования для полного факторного эксперимента
Геометрически полный факторный план при n=3 можно изобразить в виде куба, центр которого отвечает точке основного уровня факторов, а координаты вершин заданы условиями опытов. При n>3 полный факторный план геометрически означает n-мерный гиперкуб. Полные факторные планы имеют важные свойства: симметричность плана относительно центра эксперимента: 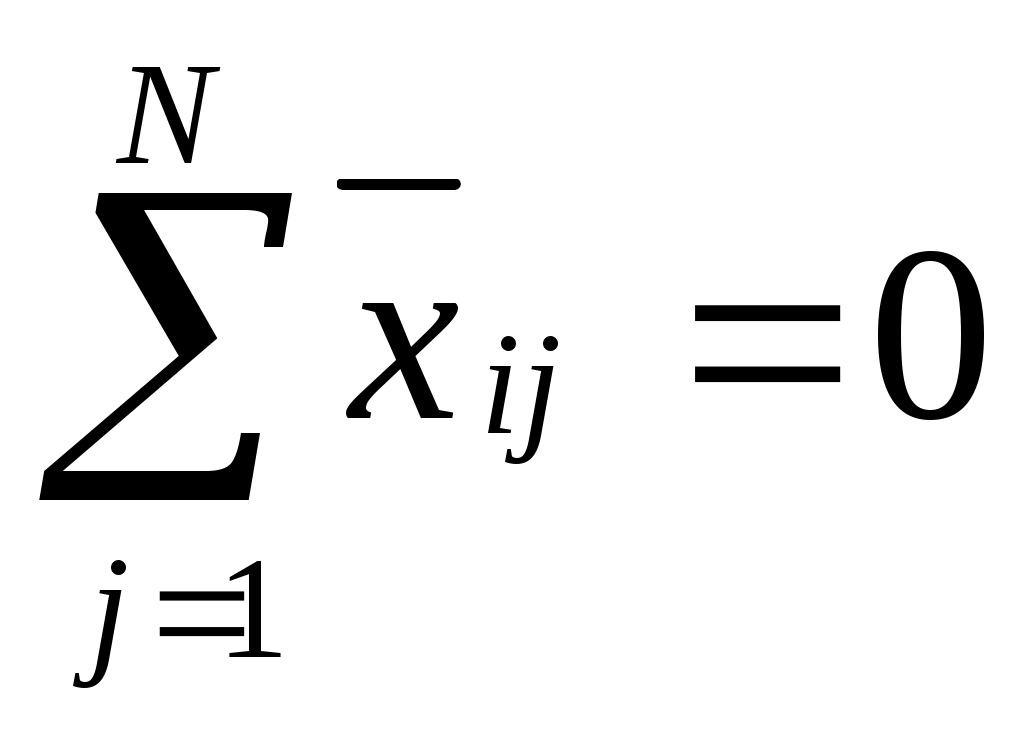 ,  , (7)где  – значение уровня і-го фактора в j-м опыте (попытке); нормированность плана: 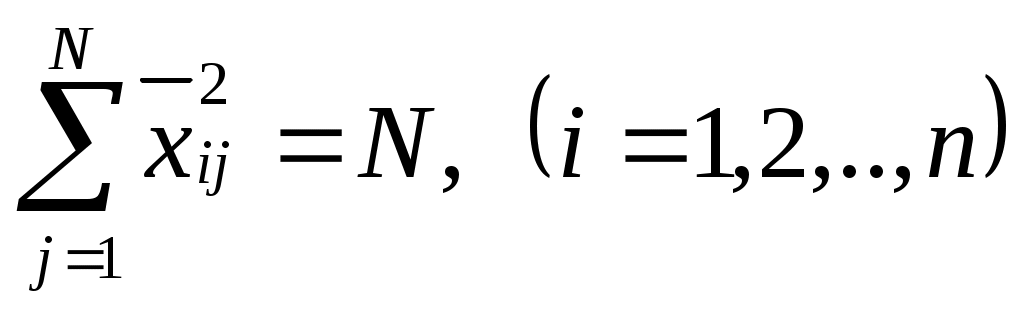 ; (8)ортогональность плана – скалярные произведения векторов-столбцов матрицы планирования равняются нулю: 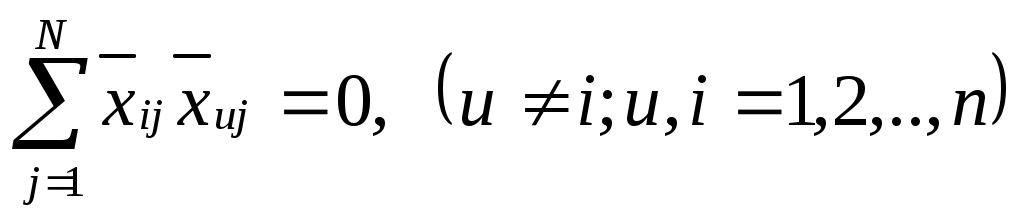 ; (9)рототабельность (от лат. roto – оборачиваюсь) плана означает, что точность предсказания значения функции отклика одинакова на равных расстояниях от центра эксперимента и не зависит от направления движения (в рототабельных планах точки факторного пространства, используемые для опытов, лежат на поверхности сферы, центром которой является точка основного уровня). Полные факторные планы дают возможность установить влияние на функцию отклика не только отдельно каждого фактора, но и их комбинаций, т.е. исследовать так называемый эффект взаимодействия. Для этого в матрицу планирования дополнительно вносят векторы-столбцы, которые содержат значение комбинаций уровней факторов (Таблица 2). Таблица 2 – Матрица планирования с эффектами взаимодействия
С целью упрощения обработки данных к матрице планирования введен фиктивный фактор  , который приобретает одно значение +1. Матрица планирования с эффектами взаимодействия сохраняет указанные выше свойства полных факторных планов.Дробный факторный эксперимент На практике довольно часто влияние эффектов взаимодействия на функцию отклика незначительно, и коэффициенты регрессии в уравнении (6) при нелинейных членах малы сравнительно с коэффициентами при линейных членах. Это означает, что функция отклика может описываться полиномом первой степени (7). Для определения такой модели нужно найти коэффициенты bi. Для этого достаточно иметь отклики в n+1 точках факторного плана, тогда как в полном факторном плане выполняется 2n попыток. Учитывая условие 2n > n+1, добытые данные будут чрезмерными. Например, при трехфакторном эксперименте для определения коэффициентов  полный факторный план дает 8 попыток, хотя достаточно провести 4 попытки. Поэтому для оценок коэффициентов в линейных аппроксимирующих полиномах используются дробные факторные планы, в которых число попыток меньше числа точек в факторном пространстве.Рассмотрим полный двухфакторный план, матрица которого приведена в таблице 3. Таблица 3 – Матрица планирования дробного факторного плана
Если пренебречь эффектом взаимодействия факторов Х1 и Х2, то вектор-столбец матрицы планирования, в котором размещены элементы произведения  , можно использовать для записи уровней третьего фактора  . Полученный при этом дробный факторный план будет иметь свойства симметричности, нормированности, ортогональности, рототабельности. Сравнивая табл. 1.2 и 1.3, можно заметить, что образованный таким способом дробный факторный план реализует первые 4 попытки (половину) полного факторного плана. Поэтому такой дробный факторный план называется полурепликой и обозначается  .Дополняющую полный факторный план полуреплику, которая реализует другую половину полного трехфакторного плана, можно получить, если в полном двухфакторном плане значения элементов (  ) присвоить уровням фактора .Для вычисления коэффициентов регрессии уравнений (7)…(9) в полных и дробных факторных планах нужно выполнить N опытов. Сначала выясняют, возможна ли линейная аппроксимация функции отклика на заданной области изменения факторов. К полиномам более высокой степени переходят в том случае, когда линейная модель неадекватна полученным исследовательским данным или нужно глубже изучить поведение функции отклика возле некоторой точки. Для уравнения линейной регрессии (9) коэффициенты вычисляются методом наименьших квадратов:   (10)В случае, когда учитывается взаимодействие факторов, коэффициенты регрессии bis определяются как:   (11)Из формул (10) и (11) видно, что для определения любого коэффициента нужны лишь соответствующие столбики матрицы планирования и столбики отклика y. Это дает возможность усложнить модель, не пересчитывая найденные раньше коэффициенты. Это обеспечивается свойством ортогональности плана. Коэффициенты регрессии bi и bis определяются для кодированных уровней факторов. Поэтому нужно перейти из пространства кодированных переменных к пространству натуральных с учетом. Например, для линейной регрессии:  (12)Для вычисления коэффициентов регрессии полинома второй степени: 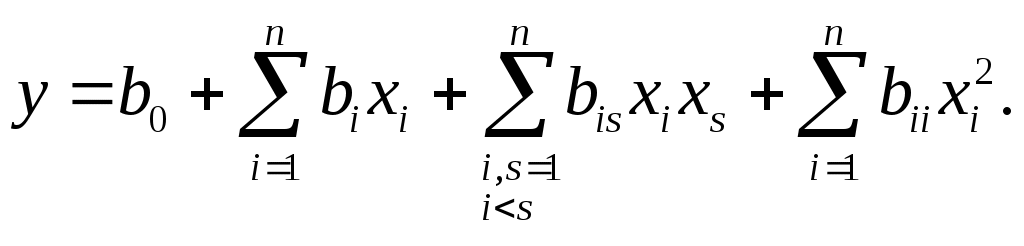 (13)двухуровневые факторные эксперименты не пригодны, так как неизвестных коэффициентов в модели (13) больше, чем попыток в полном факторном плане (например, при трех факторах число неизвестных коэффициентов будет 11, а уровней факторов ― только 23=8). Поэтому для построения полиномов второй степени нужно варьировать значение факторов, по крайней мере, уже на трех уровнях. |
