Курсовая работа ИНДИВИДУАЛЬНЫЙ ПОДХОД К УЧАЩИМСЯ В ПРОЦЕССЕ ОБУЧ. Частное образовательное учреждение высшего образования восточная экономикоюридическая гуманитарная академия (Академия вэгу)
 Скачать 234.5 Kb. Скачать 234.5 Kb.
|
1 2 2.1. Сущность принципа индивидуального подхода в дидактике Сущность принципа индивидуального подхода состоит в изучении и учёте в учебном процессе индивидуальных особенностей каждого ученика с целью максимального развития положительных и преодоления отрицательных индивидуальных особенностей, противоречащих требованиям общества, и обеспечения на этой основе всемерного повышения качества его учебной работы, всестороннего развития учащихся, расцвета их творческих способностей и дарований [3, с. 211]. Принцип индивидуального подхода к учащимся является психолого-гуманистическим принципом. Требование учитывать в учебном процессе индивидуальные особенности учащихся ни в коей мере не означает приспособления программ и общих требований обучения к особенностям каждого ученика. Это требование означает необходимость разрабатывать определённую систему воздействия на ученика с учётом индивидуальных и возрастных особенностей, имеющих целью осуществление общих задач воспитания, так и задач определённого периода обучения. В связи с тем, что именно в коллективе могут быть созданы наиболее благоприятные условия для успешного обучения и всестороннего развития каждого ученика, некоторые дидакты этот принцип называют учёт индивидуальных особенностей в коллективной работе с учащимися (Н.А. Сорокин), принцип коллективного характера обучения и учёта индивидуальных особенностей учащихся (М.А. Данилов) [6, с. 138]. Индивидуальный подход необходимо осуществлять в отношении всех учащихся, независимо от их успеваемости, поскольку каждый ребёнок представляет собой относительно более сильные или слабые стороны. Только зная индивидуальные особенности ученика, можно сознательно и уверенно руководить всесторонним формированием его личности. Изучение ребёнка, истории его жизни и развития должно быть направлено на то, чтобы уяснить, во-первых, что представляет собой ребёнок сегодня в данный момент, во-вторых, что он представлял собой в прошлом, и, в-третьих, каким он будет, должен быть завтра, т.е. видеть ребёнка в перспективе, ориентироваться на будущее, проектировать его развитие. В этом залог успешного осуществления индивидуального подхода в учебном процессе. Психологи и педагоги разработали различные примерные программы педагогического изучения учащихся. Однако какими бы различными ни были эти программы, основное содержание их сводится к следующему. Необходимо получить краткие сведения о семье ребёнка, узнать условия жизни его в семье, познакомиться с особенностями физического развития, то есть с состоянием здоровья ребёнка, изучить особенности общего и умственного развития ребёнка- его готовность учиться в данном классе, уровень познавательных способностей - наблюдательность, внимание, память, речь, мыслительные процессы, направленность интересов (к чему, к какому учебному предмету ученик проявляет наибольший интерес), качество знаний, умений и навыков по каждому предмету (в чём ученик более силён, в чём менее), отношение к учебным занятиям - к своим успехам и неудачам, навыки самостоятельности и темп работы, изучить морально волевые качества ученика - овладение правилами поведения, чувство ответственности за порученное дело, уравновешенность, настойчивость, умение преодолевать трудности. Для того чтобы получить ответы на указанные вопросы, учитель наблюдает за деятельностью учащихся на уроке и во внеурочное время, беседует с учеником, с его родителями, изучает детские работы, если нужно, проводить педагогический эксперимент. Опираясь на данные, полученные в результате изучения учащихся, учитель намечает ближайшие педагогические задачи в работе с каждым учеником. Например, в работе с одним учеником сосредоточить внимание на преодолении нерешительности и застенчивости, в работе с другим - на воспитании интереса к учёбе. Создать условия для проявления и развития индивидуальных способностей и дарований учащихся, даёт индивидуальные задания в соответствии с интересами детей, содействует поступлению детей в специальные кружки, студии. Выбирает, а затем и применяет наиболее эффективные средства индивидуального подхода к ученикам, разрабатывает систему индивидуальной работы с каждым из них. Учитель внимательно следит за результатами работы с отдельными учениками, за происходящими изменениями в их развитии, характере, в учении и в связи с этим изменяет и примеры индивидуального подхода. Принципы индивидуального подхода в дидактике предполагает учёт таких особенностей учащихся, которые влияют на его учебную деятельность и от которых зависят результаты учения. К особенностям, которые следует учитывать в первую очередь при индивидуальной работе относят [3, с. 216]:
С умственными тесно связана способность учащихся самостоятельно усваивать знания, предполагающая наличие у них соответствующих интеллектуальных умений. Последние представляют собой приёмы умственного труда, которые получили название умения умственного труда, или учебные умения. Учебные умения нагляднее всего проявляются в самостоятельной работе учащихся с учебным материалом: при восприятии и обработке нового материала, при выделении из него существенного, его структуировании и связывании нового материала с ранее пройденным, при обобщении учебного материала, повторении и его применении. Таким образом, они связаны со всей учебно-познавательной деятельностью учащихся в процессе обучения. Основное требование, предъявляемое к учителю в настоящее время, - полное использование потенциальных возможностей каждого ученика. Поэтому одним из важнейших факторов успешного усвоения программного материала каждым учеником является сочетание фронтальных и индивидуально-групповых форм работы, основанных на систематическом изучении особенностей учащихся. Перед учителем всегда стоит задача: не только видеть в каждом уроке общую учебно-воспитательную проблему, но и определять пути разрешения этой проблемы применительно к каждому ученику. школа математика индивидуальный Сочетание индивидуализации обучения с классно-урочной коллективной работой - задача весьма нелёгкая. Оно необходимо как условие, обеспечивающее работу каждого ученика в доступном ему темпе, для поощрения перехода от одного уровня развития к другому, для стимулирования способностей одних и создания перспективы другим. Индивидуальная работа должна проводиться как с сильными, так и со слабыми учащимися. В основе работы с сильными учащимися должна быть постоянно увеличивающаяся по содержанию нагрузка. При этом следует учитывать, что на активности сильных учеников особенно отрицательно сказывается однообразие и трафарет в работе. Индивидуальная работа со слабыми учащимися должна быть основана на систематическом изучении трудностей, которые они испытывают в усвоении материала. Школьная практика и специальные исследования убеждают, что у разных учащихся неуспеваемость вызывается различными причинами. Так, изучая и анализируя случаи неуспеваемости в школе, исследователи обнаружили, что у одних школьников основная причина неуспеваемости связана с неправильно сформировавшимся отношением к учению; у других основной причиной неуспеваемости является трудность усвоения ими учебного материала, то, что обычно называют неспособностью; третьи ученики не успевают потому, что не овладели правильными приёмами учебной работы; некоторые потому, что у них не развиты учебные интересы. Поскольку причины неуспеваемости различны, постольку и работа с отдельными учениками в плане преодоления неуспеваемости должна быть организована различно. Вместе с тем можно всё же говорить об общем пути реализации индивидуального подходах неуспевающим ученикам. Таким образом, индивидуальный подход к школьникам - важнейший принцип воспитания и обучения. 2.2. Применение индивидуального подхода на уроках математики Индивидуальная работа требует постоянного наблюдения, анализа и учета результатов. Она обычно включает три этапа:
Составление или подбор дифференцированных заданий, включающих различные приемы, помогающие учащимся самостоятельно справиться с заданием, или связанных с увеличением объема и сложности задания. Постоянный контроль результатов работы учащихся, в соответствии с которыми изменяется характер дифференцированных заданий. Если не будет осуществляться постоянный контроль результатов этой работы, то предлагаемые учащимся дифференцированные задания будут носить формальный характер. Учитель должен творчески подходить к использованию заданий, должен учитывать целый ряд вопросов, от которых зависит эффективность проводимой работы. Эти вопросы связаны с планированием урока, так как учителю приходится не только сочетать коллективные формы работы с индивидуальными, но и одновременно управлять учебной деятельностью нескольких групп учащихся: с местом дифференцированных заданий на уроке; с содержанием карточек с дифференцированными заданиями, с оценкой выполненных заданий, которая должна учитывать единство требований к знаниям, умениям и навыкам и индивидуальные особенности учащихся, и с целым рядом других вопросов. Особенно сложный вопрос – организация дифференцированной работы на уроке, возможности использования дифференцированного подхода к учащимся при работе над ошибками в процессе обучения решению задач. Эту работу можно организовать следующим образом. На одном уроке даются две-три задачи для самостоятельного решения. После проверки работы делается их анализ (отметки за эту работу не выставляются). На другом уроке предлагаются дифференцированные задания для всех учащихся. При составлении дифференцированных заданий нужно ориентироваться на те умения, которые должны быть сформированы у учащихся в процессе решения задач, это умения [2, с. 67]: - прочитать задачу, осознать ее текст, выделить условие и вопрос; - выделить данные и искомое задачи и установить между ними связь; - выбрать арифметическое действие для решения задачи; - записать решение и ответ задачи; - проверить решение задачи. Учитываются также те трудности, которые возникли у учащихся при самостоятельном решении задач. Учащимся, которые успешно справились с решением задач, предлагаются дифференцированные задания, которые связаны с увеличением объема заданий, с повышением сложности задач, с составлением обратных задач, с решением задач с недостающими и лишними данными, с составление задач по данному решению. Ошибки учащихся нужно соотнести с несформированностью тех или иных умений. Проследим на конкретном примере. Коробка цветных карандашей стоит 42 рубля, кисточка в 3 раза дешевле коробки карандашей, а книга на 28 рублей дороже, чем кисточка. Сколько стоит книга? Хозяйка купила 16 кг огурцов. Она разложила их в 4 банки по 3 кг огурцов в каждую. Сколько килограммов огурцов у нее осталось? Хозяйка купила 3 м шелка по 200 рублей за 1 м, и столько же метров шерсти по 400 рублей за 1 м. Сколько денег она уплатила за покупку? При анализе работы выделяются следующие ошибки: Ошибки, связанные с непониманием текста задачи. Например, в задаче №1 учащиеся выполнили первое действие так: 42*3 (ошибочно считая, что дешевле это больше), а второе 126-28. Ошибки, причиной которых явилось неумение учащихся устанавливать взаимосвязь между данными и искомым задачи. Например, некоторые учащиеся решили задачу №2 по действиям так: 1) 16:4, 2) 3*4, 3) 16-4. Эта ошибка, безусловно, связана с непониманием взаимосвязи между данными и искомым задачи. Решение задачи №3 некоторые учащиеся выполнили так: 3*200+400. Эта ошибка опять же связана с неумением внимательно прочитать текст задачи. Некоторые ученики вообще не приступали к решению третьей задачи или допустили ошибки в вычислении и обозначении величин. В результате полученных данных составим следующую таблицу. Таблица 1. Таблица результатов решения задач по математике
Таким образом, полностью с задачами справились 5 учеников, допустили ошибки 4 ученика (в основном связанные с ошибками в вычислениях). 75% учащихся понимают текст задачи, умеют устанавливать взаимосвязь между данными и искомым задачи, правильно обозначают величины. 67% учащихся правильно определяют порядок действий. 42 % учащихся не имеют ошибок в вычислениях (однако 58 % допускают ошибки в вычислениях, для них требуется отработать навык вычислений). Полностью не справились с задачами 3 ученика. Таким образом, 25% учащихся не умеют решать задачи. С учетом этого, можно составить дифференцированные задания. Ученикам, которые самостоятельно справились с решением всех трех задач, предлагаются следующие задания: 1.Решите задачу: «За три стула заплатили 180 рублей. Сколько стульев можно купить на 360 рублей? Сформулируйте вопрос задачи так, чтобы ответ на него был найден умножением. На какие вопросы можно еще ответить, пользуясь данными задачи №1? Запишите эти вопросы и ответьте на них. 2. Прочитайте задачу № 2. Во сколько банок можно разложить оставшиеся огурцы и сколько килограммов огурцов останется после этого? 3. Решите задачу: «Хозяйка купила 3 м шелка по 200 рублей за 1м, шерсти на 2м больше, 1м шерсти стоит 400 рублей». Поставьте вопросы к данному условию и решите задачу. 4. Составьте обратную задачу к задаче №1 и решите ее. Для учеников, допустивших ошибки, предлагаются такие дифференцированные задания: Со вспомогательными вопросами. К задаче №2. Ответьте на вопросы: что означает число 3 в условии задачи? (3 кг огурцов в одной банке). Можно ли узнать, сколько килограммов огурцов в 4-х банках? (Можно. 3*4=12кг). Хозяйка купила огурцов больше или меньше, чем 12 кг? (Больше). Запишите теперь решение задачи. К задаче №3. Прочитайте внимательно условие задачи. Что означает столько же метров шерсти? Запишите эти слова числом (3 м шерсти по 400 рублей за 1 м) и решите задачу. С дополнительными указаниями. К задаче №1. Дешевле – значит меньше; дороже - значит больше. Замените слова дороже и дешевле словами больше и меньше и решите задачу. К задаче №2. Узнайте сначала, сколько килограммов огурцов в 4-х банках, а затем ответьте на вопрос задачи. К задаче №3. Узнайте сначала, сколько стоит шелк, а затем - сколько стоила шерсть, а потом ответьте на вопрос задачи. С выполнением некоторой части задания: К задаче №1. Закончите решение задачи: 1). 42:3=12 (руб.) Запишите первое действие и ответ задачи. 1). 2). 12+28=___ (коп.) К задаче №2 1). 3*___=___ (кг) 2). ___-___=___ (кг) Запишите решение задачи, пользуясь схемой. Запишите ответ. Для самостоятельного решения можно дать не три, а одну задачу и после анализа ее провести дифференцированную работу с учащимися. Предлагается классу самостоятельно решить задачу и записать ее решение по действиям: «Класс должен подклеить 80 книг. Первая группа подклеила 16 книг, вторая 18 книг. Сколько книг осталось подклеить?» Работу пишут 12 учеников. Через пять минут можно пройти по рядам и увидеть, например, что 9 учеников работу выполнили, а 3 ученика не решили. На доске открывается краткая запись задачи: Было - 80 кн. Сделали - 16 кн. И 18 кн. Осталось - ? Предлагается ученикам, которые не успели выполнить задание, внимательно рассмотреть краткую запись. Объясняется, что эта запись поможет им справиться с решением задачи. Тем, кто выполнил задание, предлагается записать решение задачи выражением. В результате ученики самостоятельно записывают задачу выражением. 1 ученик не может этого сделать. На доске дается выражение 80-(16+18) и предлагается одному ученику, справившемуся с заданием, объяснить его. После решения дифференцированных заданий составим таблицу. Таблица 2. Таблица результатов решения задач по математике
После использования дифференцированных заданий, мы видим, что у учащихся повысился уровень знаний по математике. Так, полностью справились с задачами 9 учеников, проблемы с решениями остались у 3 учеников. 100% учащихся понимают текст задачи, умеют устанавливать взаимосвязь между данными и искомым задачи, правильно обозначают величины. 80% учащихся правильно определяют порядок действий. 75 % учащихся не имеют ошибок в вычислениях. Детей, которые не справились совсем – нет. В основном, остались проблемы, связанные с вычислениями. Итак, можно сделать вывод, что данная методика организации дифференцированных заданий оказывается эффективной. Именно анализ выполненных учащимися работ помогает определить, какое дифференцированное задание следует предложить тому или иному ученику. ВЫВОД ПО ГЛАВЕ 2 Индивидуальный подход к каждому учащемуся состоит в изучении и учете во время учебного процесса личностных особенностей каждого ученика, независимо от его успеваемости, с целью максимального развития его творческих и мыслительных способностей, обеспечении всестороннего развития учащихся, расцвете их талантов и возможного исправления отрицательных качеств, противоречащих требованиям общества. Индивидуальный подход к каждому учащемуся — это один из современных методов повышения качества обучения математике, при котором учитель контролирует знания каждого ребенка и может, в зависимости от индивидуальных способностей ученика принимать меры по их улучшению. При этом изложение учебной программы должно быть построено так, чтобы стимулировать учащихся к самостоятельной работе и давать возможность выбора при выполнении работ. Эффективность подобного обучения математики можно оценить по следующим параметрам:
Система индивидуального подхода к обучению создает оптимальные условия, способствующие развитию личности ученика. Таким образом, осуществляя индивидуальный подход к учащимся, изучая и зная их способности и склонности, учителю необходимо планировать использование индивидуализированных средств обучения, позволяющих подбирать соответствующие задания каждому ученику. ЗАКЛЮЧЕНИЕ Таким образом, мы можем выделить следующие особенности начального курса математики: - основой начального курса является арифметика натуральных чисел и основных величин; - материал начального курса математики вводится концентрически; - вопросы теоретического и практического характеров органически связываются между собой; - математические понятия, свойства и закономерности раскрываются в курсе в их взаимосвязи; - начальный курс математики построен так, чтобы в процессе его изучения каждое понятие получило развитие; - сходные или связанные между собой вопросы рассматриваются в сравнении. Выделяются следующие основные понятия начального курса математики: - арифметические действия; - понятие натурального числа; - число нуль и цифра 0; - наглядное представление о дроби; - свойства арифметических действий; - система упражнений для выработки вычислительных навыков; - элементы алгебры и геометрический материал; - понятие величины и идея измерения величин; - решение задач. Индивидуальный подход к каждому учащемуся состоит в изучении и учете во время учебного процесса личностных особенностей каждого ученика, независимо от его успеваемости, с целью максимального развития его творческих и мыслительных способностей, обеспечении всестороннего развития учащихся, расцвете их талантов и возможного исправления отрицательных качеств, противоречащих требованиям общества. Индивидуальный подход к каждому учащемуся — это один из современных методов повышения качества обучения математике, при котором учитель контролирует знания каждого ребенка и может, в зависимости от индивидуальных способностей ученика принимать меры по их улучшению. При этом изложение учебной программы должно быть построено так, чтобы стимулировать учащихся к самостоятельной работе и давать возможность выбора при выполнении работ. Эффективность подобного обучения математики можно оценить по следующим параметрам:
Система индивидуального подхода к обучению создает оптимальные условия, способствующие развитию личности ученика. Таким образом, осуществляя индивидуальный подход к учащимся, изучая и зная их способности и склонности, учителю необходимо планировать использование индивидуализированных средств обучения, позволяющих подбирать соответствующие задания каждому ученику. СПИСОК ЛИТЕРАТУРЫ
Приложение 1 Фрагмент конспекта урок. Рассмотрим фрагмент урока математики с целью определения места проведения индивидуальной работы на уроке и осуществления индивидуального подхода к учащимся с целью активизации их деятельности. КЛАСС: 3 класс ТЕМА: Таблицы умножения и деления с числом 7. ЦЕЛЬ: Составить таблицы умножения с числом 7 и на 7, составить соответствующие таблицы деления.
На этом уроке осуществляется индивидуальный подход к учащимся на этапе изучения нового материала. Часть учащихся самостоятельно работает по составлению таблиц умножения и деления с числом 7. Слабые учащиеся работают вместе с учителем. В ходе этой работы активизируется мыслительная деятельность учащихся дополнительными вопросами. Учитываются психические особенности детей: дополнительные вопросы адресуются невнимательным, рассеянным ученикам, ученик с хорошей моторной памятью вызывается к доске. На этапе первичного закрепления проводится небольшая самостоятельная работа с целью проверки усвоения материала большинством детей. Индивидуальный подход осуществляется с помощью дифференцированных заданий. Приложение 2 Самостоятельные работы с дифференцированными заданиями по закреплению навыков табличного умножения и деления.Самостоятельная работа Общие задания
82 – 7 . 7 42 : 7 + 63 : 9 9 . 7+ 1. 7 50 – 6 . 7 28 : 4 + 49 : 7 8 . 7 + 8 . 3 35 – 3 . 9 5 . 7 – 3 . 5
Отправляясь на экскурсию, ученики построились по четыре человека в ряду, а рядов было девять. На обратном пути они шли по шесть человек в ряду. Во сколько рядов построились ученики на обратном пути. Карточка в помощь «слабым» учащимся.
Туда – 9 рядов на 4 человека Обратно ? по 6 человек
Реши задачу. Проверь себя, подставив в выражения числовые данные: Карточка с дополнительным заданием «сильным» ученикам. Подчеркните выражения, в которых нужно найти сумму двух произведений. Как записать эти выражения короче, заменив умножением числа на сумму. Самостоятельная работа Задания «слабым» ученикам
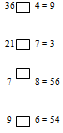
8 см. 4 мм. = … мм. 2 дм. 6 см. = … см. 5 м. 8 дм. = … дм. 4 см. 2 мм. = … мм. Задания «средним» ученикам1. Вставьте пропущенные числа 36 : = 9 . 6 = 54 21 : = 3 : 9 = 8 : 8 = 56 . = 36 2. Сравните, поставьте знак >,< или = 3 м. 8 дм. …. 39 дм. 6 дм. 3 см. … 36 см. 81 дм. …. 8 м. 1 дм. 17 мм. …. 1 см 9 мм. Задания «сильным» ученикам
36 : 4 … = 18 28 : 4 … = 14 72 : 9 … = 56 6 . 8 … = 29
8 см. 4 мм. < … мм. … м …. дм. < 81 дм. 5 м. … дм. > … м 7 дм. 3 м 8 дм. > … дм Приложение 3 Индивидуальная самостоятельная работа Данная самостоятельная работа проводится с целью совершенствования навыков табличного умножения и деления.
1 2 |
