Числовые системы
 Скачать 1.01 Mb.
|
Вторая замечательная точка треугольникаТ 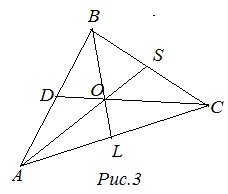 очка пересечения серединных перпендикуляров сторон треугольника (рис. 2)Эта точка и есть центр описанной около треугольника окружности, находится в треугольниках с острыми углами, вне треугольника с тупым углом и на гипотенузе прямоугольного треугольника. Третья замечательная точка треугольникаТочка пересечения медиан (рис. 3). Т 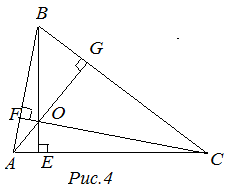 ЕОРЕМА : Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.Точка пересечения медиан является центром тяжести треугольника. Четвёртая замечательная точка треугольника Точка пересечения высот треугольника (рис. 4)ТЕОРЕМА : Высоты треугольника или их продолжения пересекаются в одной точке. Точку пересечения высот называется ортоцентромтреугольника. 30. Замечательные линии в треугольнике. Медиана треугольника – это отрезок, который связывает вершину треугольника с серединой одной из сторон данного треугольника. Свойства медиан треугольника Медиана делит треугольник на два треугольника, площади которых одинаковы.Медианы треугольника пересекаются только в одной точке, которая разделяет каждую из них в отношении 2 : 1, отсчитывая от вершины. Такая точка именуется центром тяжести треугольника. В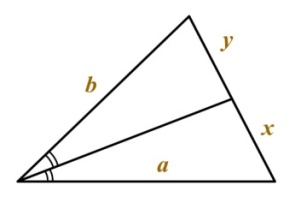 есь треугольник разбивается своими медианами на шесть равных по значению треугольников. Биссектриса угла – это исходящий из вершины угла луч, пролегающий между образующими сторонами и разделяющий его пополам.Свойства биссектрис треугольникаБиссектриса угла – есть геометрическое место точек, которые равноудалены от сторон этого угла.Биссектриса угла треугольника, разделяет противолежащую сторону на отдельные отрезки, которые пропорциональны прилежащим сторонам:В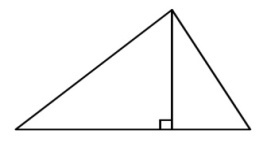 точке, где пересекаются биссектрисы треугольника, находится центр окружности, который вписан в этот треугольник. Высотой треугольника называется линия, проведенная из вершины треугольника к одной из сторон расположенной перпендикулярно. С 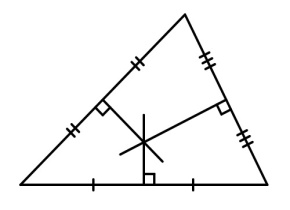 войства высот треугольникаПерпендикулярная линия высотыпрямоугольного треугольника разделяет его на два подобных ему треугольника.Две линии высоты остроугольного треугольника, отделяют от него подобные треугольники.Срединный перпендикуляр Перпендикулярная прямая, которая проходит через середину отрезка, называется – срединный перпендикуляр к отрезку.Свойства серединных перпендикуляров треугольника Все точки серединного перпендикуляра к отрезку равноудалены от окончаний этого отрезка. Верно так же и обратное утверждение, что каждая точка, находящаяся на равных расстояниях от концов отрезка, расположена на серединном перпендикуляре к нему. В точке пересечения серединных перпендикуляров, проведенных в направлении к одной из сторон треугольника, находится центр окружности, который описывает данный треугольник.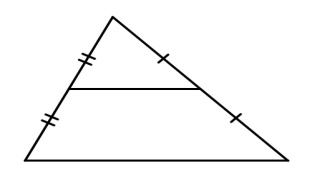 Отрезок, который соединяет две стороны треугольника в их серединах, называется – средняя линия треугольника. Свойство средней линии треугольника |