Числовые системы
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
Некоторые следствия из аксиомТеорема 1.Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна. Теорема 2. Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна. Параллельные прямые в пространствеДве прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна. Лемма о пересечении плоскости параллельными прямыми. 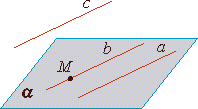 Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.Теорема о трех прямых в пространстве. Если две прямые параллельны третьей прямой, то они параллельны (если a∥c и b∥c, то a∥b). П 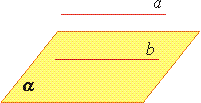 араллельность прямой и плоскости араллельность прямой и плоскостиПрямая и плоскость называются параллельными, если они не имеют общих точек. Признак параллельности прямой и плоскости Теорема.Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. Теорема. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. Теорема. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости. 37. Многогранники. Выпуклый многогранник. Кратко охарактеризуем геометрические свойства некоторых многогранников:
  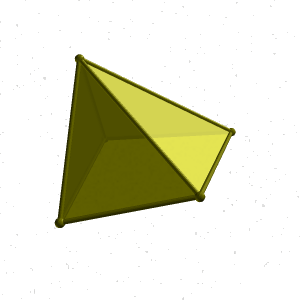 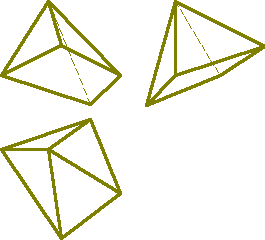 .Пирамида- это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной. Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина её отсекается плоскостью (рис.67). .Пирамида- это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной. Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина её отсекается плоскостью (рис.67).
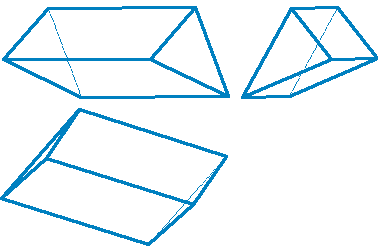
 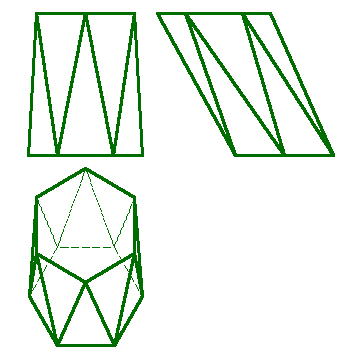 .Призма- многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом (рис. 68). .Призма- многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом (рис. 68). 3.Призматоид- многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой треугольники или трапеции, вершины которых являются и вершинами многоугольников оснований (рис.69). 4.Тела Платона. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными. Углы при вершинах такого многогранника равны между собой.
 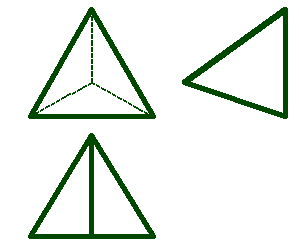 уществует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название. уществует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название. Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково. Тетраэдр- правильный четырехгранник (рис.70). Он ограничен четырьмя равносторонними треугольниками (это - правильная треугольная пирамида).
  ексаэдр- правильный шестигранник (рис. 71). Это куб состоящий из шести равных квадратов. ексаэдр- правильный шестигранник (рис. 71). Это куб состоящий из шести равных квадратов.
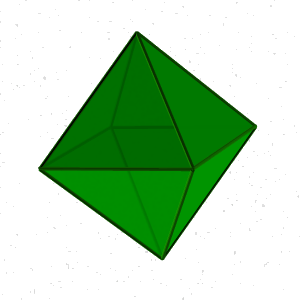
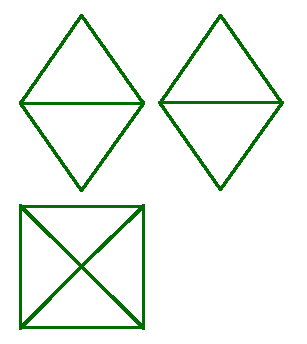
   ктаэдр- правильный восьмигранник (рис.72). Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины. ктаэдр- правильный восьмигранник (рис.72). Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.
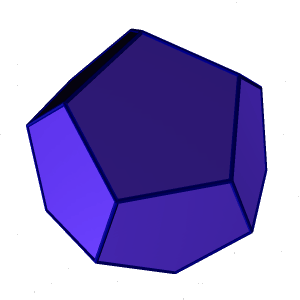
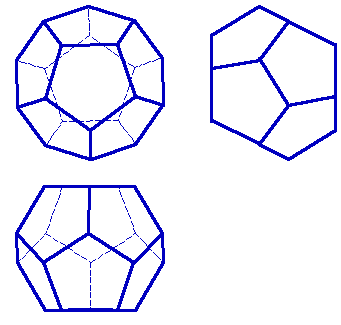
  одекаэдр- правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины (рис. 73). одекаэдр- правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины (рис. 73). Икосаэдр- состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины (рис.74). 5.Звездчатые формы и соединения тел Платона.Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники. Звездчатый октаэдр - восемь пересекающихся плоскостей граней октаэдра отделяют от пространства новые "куски", внешние по отношению к октаэдру (рис.75). Это малые тетраэдры, основания которых совпадают с гранями октаэдра. Его можно рассматривать как соединение двух пересекающихся тетраэдров, центры которых совпадают с центром исходного октаэдра. Все вершины звездчатого октаэдра совпадают с вершинами некоторого куба, а ребра его являются диагоналями граней (квадратов) этого куба. Дальнейшее продление граней октаэдра не приводит к созданию нового многогранника. Октаэдр имеет только одну
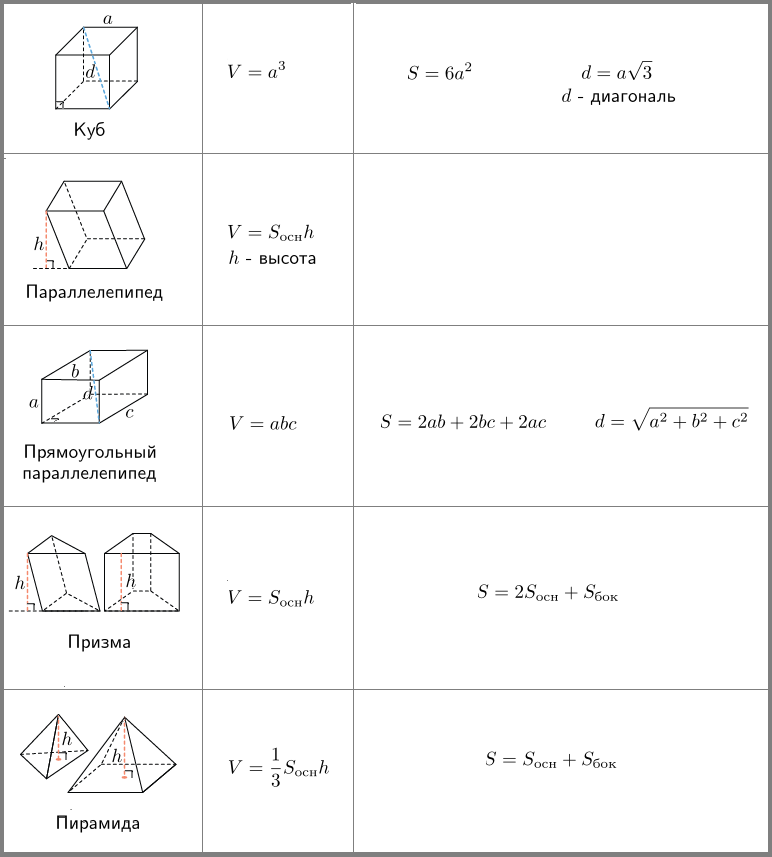  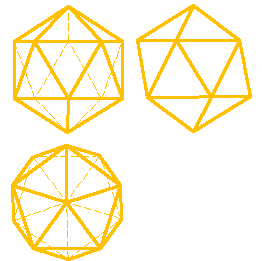 вездчатую форму. Такой звездчатый многогранник в 1619 году описал Кеплер (1571-1630) и назвал его stellaoctangula - восьмиугольная звезда. вездчатую форму. Такой звездчатый многогранник в 1619 году описал Кеплер (1571-1630) и назвал его stellaoctangula - восьмиугольная звезда.
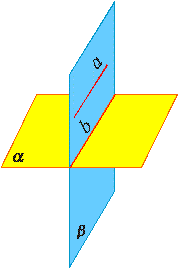
В 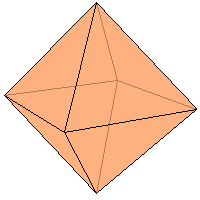 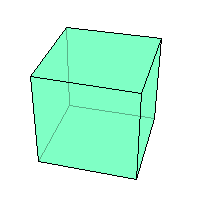 ыпуклый многогранник ыпуклый многогранникМногогранник называется выпуклым, если он расположен по одну сторону от каждой из плоскостей, содержащих его грани ПРИМЕРЫ: Октаэдр - выпуклый многограник: Куб - выпуклый многограник: 38. Площади поверхностей многогранников. Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб». Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту. Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы. Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию. 39. Понятие площади поверхности. Площадью поверхности многогранника называется сумма площадей многоугольников, из которых состоит поверхность многогранника, т.е. сумма площадей граней многогранника. Пусть Ф − гладкая ограниченная поверхность. Разобьем ее с помощью кусочно гладких кривых на конечное число n частей Фi (i = 1, 2, …, n) так, чтобы каждая часть Фi однозначно проектировалась на касательную плоскость, проведенную в любой точке этой части (предполагается, что такое разбиение возможно). На каждой части Фi возьмем произвольную точку Mi и проведем через нее касательную плоскость к поверхности. Обозначим через Si площадь проекции Фi на касательную плоскость (эта проекция ограничена кусочно гладкими кривыми и потому квадрируема). Составим сумму S(Фi, Mi) = 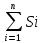 . Пусть di − диаметр Фi, d = . Пусть di − диаметр Фi, d = 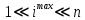 di. Определение . Число S называется пределом сумм S(Фi, Mi) при d → 0, если ∀ ε > 0 ∃ d > 0 такое, что для любого разбиения поверхности Ф, у которого d < δ, и для любого выбора точек Mi выполняется неравенство |S(Фi, Mi) − S| < ε. di. Определение . Число S называется пределом сумм S(Фi, Mi) при d → 0, если ∀ ε > 0 ∃ d > 0 такое, что для любого разбиения поверхности Ф, у которого d < δ, и для любого выбора точек Mi выполняется неравенство |S(Фi, Mi) − S| < ε. Если существует 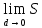 (Фi, Mi) = S, то поверхность Ф называется квадрируемой, а число S − площадью поверхности Ф. (Фi, Mi) = S, то поверхность Ф называется квадрируемой, а число S − площадью поверхности Ф. Замечание 1 . Поверхность, составленная из нескольких гладких поверхностей, называется кусочно гладкой. Если каждая из этих гладких поверхностей квадрируема, то сумма их площадей принимается за площадь кусочно гладкой поверхности. Замечание 2 . Определение площади естественным образом распространяется на поверхности, не имеющие касательной плоскости и нормали в конечном числе внутренних точек. Примером такой поверхности является коническая поверхность, которая не имеет касательной плоскости в своей вершине. 40. Площади поверхности тел вращения. Тела вращения, изучаемые в школе, — это цилиндр, конус и шар. Н  апример, такой важный факт: Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем — в 8 раз. апример, такой важный факт: Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем — в 8 раз. (ведь 41. Введение координат на плоскости и в пространстве. Возьмем три взаимно перпендикулярные прямые х, у, z, пересекающиеся в одной точке О (рис. 378). Проведем через каждую пару этих прямых плоскость. Плоскость, проходящая через прямые x и y, называется плоскостью ху. Две другие плоскости называются соответственно xz и yz. Прямые х, у, z называются координатными осями (или осями координат), точка их пересечения О — началом координат, а плоскости ху, yz и xz — координатными плоскостями. Точка О разбивает каждую из осей координат на две полупрямые — полуоси, которые мы условимся называть положительной и отрицательной. Возьмем теперь произвольную точку А и проведем через нее плоскость, параллельную плоскости yz (рис. 379). Она пересекает ось X в некоторой точке Аx. К 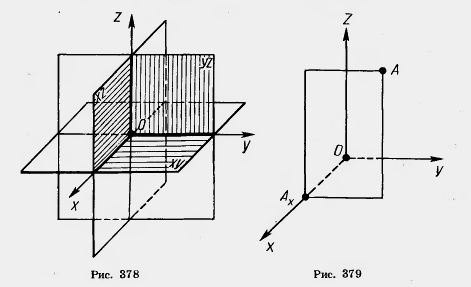 оординатой х точки А будем называть число, равное по абсолютной величине длине отрезка ОАx положительное, если точка Аx лежит на положительной полуоси X, и отрицательное, если она лежит на отрицательной полуоси. Если точка Ах совпадает с точкой О, то полагаем x = 0. Аналогично определяются координаты у и z точки А. Координаты точки будем записывать в скобках рядом с буквенным обозначением точки: А (х; у; z). Иногда будем обозначать точку просто ее координатами (х; у; z). оординатой х точки А будем называть число, равное по абсолютной величине длине отрезка ОАx положительное, если точка Аx лежит на положительной полуоси X, и отрицательное, если она лежит на отрицательной полуоси. Если точка Ах совпадает с точкой О, то полагаем x = 0. Аналогично определяются координаты у и z точки А. Координаты точки будем записывать в скобках рядом с буквенным обозначением точки: А (х; у; z). Иногда будем обозначать точку просто ее координатами (х; у; z).Задача (2). Даны точки А (1; 2; 3), В(0; 1; 2), С(0; 0; 3), D(l; 2; 0). Какие из этих точек лежат: 1) в плоскости ху; 2) на оси z; 3) в плоскости yz? Решение. У точек плоскости ху координата z равна нулю. Поэтому только точка D лежит в плоскости ху. У точек плоскости yz координата х равна нулю. Следовательно, точки В и С лежат в плоскости yz. У точек на оси Z две координаты (х и у) равны нулю. Поэтому только точка С лежит на оси z. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||


