Числовые системы
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
|
14. Арифметический треугольник. Т  реугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Числа, составляющие треугольник Паскаля, возникают естественным образом в алгебре, комбинаторике, теории вероятностей, математическом анализе, теории чисел. реугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Числа, составляющие треугольник Паскаля, возникают естественным образом в алгебре, комбинаторике, теории вероятностей, математическом анализе, теории чисел.Биномиальные коэффициенты часто обозначаются 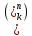 или или 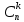 и читаются как «число сочетаний из nэлементов по k». (В математике биномиальные коэффициенты — это коэффициенты в разложении бинома Ньютона (1+х)n по степеням х.) и читаются как «число сочетаний из nэлементов по k». (В математике биномиальные коэффициенты — это коэффициенты в разложении бинома Ньютона (1+х)n по степеням х.)Числа треугольника симметричны (равны) относительно вертикальной оси. В строке с номером n: первое и последнее числа равны 1. второе и предпоследнее числа равны n. третье число равно треугольному числу 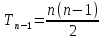 ,что также равно сумме номеров предшествующих строк. ,что также равно сумме номеров предшествующих строк.четвёртое число является тетраэдрическим. m-е число (при нумерации с 0) равно биномиальному коэффициенту 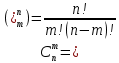 Сумма чисел восходящей диагонали, начинающейся с первого элемента (n-1)-й строки, есть n-е число Фибоначчи: 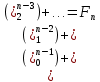 {\displaystyle {n-1 \choose 0}+{n-2 \choose 1}+{n-3 \choose 2}+\ldots =F_{n}.} {\displaystyle {n-1 \choose 0}+{n-2 \choose 1}+{n-3 \choose 2}+\ldots =F_{n}.}Если вычесть из центрального числа в строке с чётным номером соседнее число из той же строки, то получится число Каталана. Сумма чисел n-й строки треугольника Паскаля равна 2n Все числа в n-й строке, кроме единиц, делятся на число n, тогда и только тогда, когда n является простым числом (следствие теоремы Люка). Если в строке с нечётным номером сложить все числа с порядковыми номерами вида 3n, 3n+1, 3n+2, то первые две суммы будут равны, а третья на 1 меньше. Каждое число в треугольнике равно количеству способов добраться до него из вершины, перемещаясь либо вправо-вниз, либо влево-вниз. 13. Разложение бинома. Формула нахождения коэффициентов бинома Ньютона. Выведем формулу, позволяющую возводить двучлен (бином) (а+b) в любую целую неотрицательную степень. Это формула бинома Ньютона. Она имеет следующий вид: Легко убедиться, что хорошо известные формулы сокращенного умножения для (a + b)2 и (a + b)3 представляют собой частные случаи формулы бинома Ньютона. 12. Аксиомы Пеано. Метод математической индукции. 1. во мн. N существует элемент, непосредственно не следующий ни за каким элементом этого множества. 2. Для каждого элемента а из мн.N существует единственный элемент а’,непосредственно следующий за а. 3.для каждого элемента а из мн.N существует не более одного элемента, за которым непосредственно следует а. 4.если подмн.М мн.N содержит число 1 и из того, что элемент а €М, следует, что и элемент а`€М, то мн.М совпадает с мн.N. Мн.N, удовлетворяющее аксиомам 1-4, называют мн.нат.чисел, а элементы мн.N называют нат.числами.4 аксиому называют аксиомой индукции. Метод матем. индукции- это метод док-ва, основанный на принципе матем.индукции и применяемый для утверждений вида Р(п). Принцип: если утверждение Р(п) с переменной п истинно для п=1 и из того, что оно истинно для произвольного числа п=k, следует, что оно истинно и для следующего за ним числа п= k+1, то утверждение Р(п) истинно для любого натурального числа п. Док-во м.матем.нндукции состоит из трёх частей: проверяют истинность утверждения Р(п) при п, равном 1, то есть проверяют Р(1). предполагают истинность утверждения Р(п) при п, равном k, то есть предполагают истинность Р(k). на основании предположения доказывают истинность утверждения при п= k+1, то есть доказывают истинность импликации Р(k)=>Р(k+1). Вывод: утверждение Р(п) истинно для любого натурального п. Пример:док-ть, что для любого натурального числа п верно равенство 1+2+3+…+(2п-1) =п2. Док-во: при п=1 равенство имеет вид 1=12. Оно верное. Предположим, что при п= k верно следующее равенство: 1+2+3+ …+ (2 k-1) = k2. На основании предположения докажем, что при п= k+1 будет верным равенство: 1+2+3+ ..+(2 k-1)+ (2(k+1)-1) =( k+1)2. Преобразуем левую часть равенства и покажем, что она совпадает с правой частью. В самом деле, по предположению сумма 1+2+3+ …+ (2 k-1) равна k2, тогда левая часть равенства будет иметь вид: k2+2(k+1)-1 = k2+ 2k+1= (k+1)2. Видим, что левая и правая части равенства совпадают. Таким образом, из предположения о верности данного равенства при п= k доказана верность его при п= k+1. Следовательно, на основании принципа матем.индукции данное равенство верно при любом натуральном п. Метод математической индукции является важным способом доказательства предложений ( утверждений ), зависящих от натурального аргумента. Метод математической индукции состоит в следующем : Предложение ( утверждение ) Р(n), зависящие от натурального числа n, справедливо для любого натурального n если : P(1) является истинным предложением ( утверждением); 1. P(n) остается истинным предложением (утверждением), если n увеличить на единицу, то есть P ( n+1 ) – истинное предложение ( утверждение) Таким образом метод математической индукции предполагают два этапа : 1. Этап проверки: проверяется, истинно ли предложение ( утверждение ) P (1) 2. Этап доказательства: предполагается, что предложение P (n) истинно, и доказывается истинность предложения P ( n+1 ) ( n увеличению на единицу. Замечание. В некоторых случаях метод математической индукции используется в следующей форме : Пусть m – натурально число, m > 1 и P(n) – предложение, зависящее от n, n ≥ m Если: 1. P (m) справедливо; 2. P (n) будучи истинным предложением, влечет истинность предложения P ( n+1 ) для любого натурального числа n, n ≥ m, тогда P (n) – истинное предложение для любого натурального n, n ≥ m. 8-9. Позиционные и непозиционные системы счисления. Основание позиционной системы счисления . Представление чисел в виде систематической записи. Основанием позиционной системы счисления называется возводимое в степень целое число, котороеравно количеству цифр, используемых для изображения чисел в данной системе счисления. Основание показывает также, во сколько раз изменяется количественное значение цифры при перемещении ее на соседнюю позицию. Возможно множество позиционных систем, так как за основание системы счисления можно принять любое число не меньшее 2. Наименование системы счисления соответствует ее основанию (десятичная, двоичная, восьмеричная, шестнадцатеричная и т. д.). В позиционных системах счисления количественный эквивалент (значение) цифры зависит от ее места (позиции) в записи числа. Система счисления (Нумерация) - это способ представления числа символами некоторого алфавита, которые называются цифрами. Путем длительного развития человечество пришло к двум видам систем счисления: позиционной и не позиционной. Непозиционная система счисления В самой древней нумерации употреблялся лишь знак "|" для единицы, и каждое натуральное число записывалось повторением символа единицы столько раз, сколько единиц содержится в этом числе. Сложение в такой нумерации сводилось к приписыванию единиц, а вычитание - к их вычеркиванию. Для изображения сколько – нибуть больших чисел этот способ нумерации непригоден из - за своей громоздкости. При начальном обучении в школе, когда счет ведется в пределах одного - двух десятков, этот способ нумерации успешно применяется (счет на палочках). В непозиционных системах счисления смысл каждого знака сохраняется и не зависит от его места в записи числа. К более современным непозиционным системам относят египетскую иероглифическую систему нумерации, в которой имелись определенные знаки для чисел: единица - I, десять - n, сто - ρ и так далее; эти числа называются узловыми. Все остальные натуральные числа, называемые алгоритмическими числами, записываются единообразно при помощи единственной арифметической операции - сложения. Например ,число 243 запишется в виде ρρ nnnn III, 301 - в виде ρρρ I. К непозиционным системам относят римскую нумерацию. За узловые числа в этой системе принимают числа: единица - I, пять - V, десять - X, пятьдесят - L, сто - С, пятьсот - D, тысяча - М. Все алгоритмические числа получаются при помощи двух арифметических операций: сложения и вычитания. Вычитание производится тогда, когда знак, соответствующий меньшему узловому числу, стоит перед знаком большего узлового числа, например, VI - шесть (5+1= 6), ХС – девяносто(100-10=90), 1704 - МОССIV, 193 -СХСШ, 687 - DCLXXXII. В римской нумерации заметны следы пятеричной системы счисления, так как в ней имеются специальные знаки для чисел 5, 50 и 500. При записи чисел использовался не только принцип сложения, но и принцип умножения. Например, в старо — китайской системе счисления числа 20 и 30 изображались схематически, как 2,10 и 3,10. числа 10, 100, 1000 имели определенные специальные обозначения. Число 528 записывалось так: 5,100,2,10,8. Наиболее удобными среди непозиционных систем счисления являются алфавитные системы нумерации. Примерами таких систем могут служить ионийская система (Древняя Греция), славянская, еврейская, грузинская и армянская. Во всех алфавитных системах существенным является обозначение специальными символами - буквами в алфавитном порядке всех чисел от 1 до 9, всех десятков от 10 до 90 и всех сотен от 100 до 900. Чтобы отличать запись чисел от слов над буквами, обозначающими цифры, в греческой и славянской нумерации ставилась черта. В греческой системе счисления число 543 записывалось: φμγ (φ - 500, μ- 40, γ- 3). В римской системе счисления это число записывается в виде DXLIII, в египетской иероглифической - в виде ρρρρρ nnn III. Из этого примера видно преимущество алфавитной нумерации, в которой используется цифровой принцип обозначения единиц, десятков, сотен. В Наиболее удобными системами счисления оказались позиционные или поместные системы. Позиционные системы счисления Позиционная система счисления - это совокупность определений и правил, позволяющих записывать любое натуральное число с помощью некоторых значков или символов, каждый из которых имеет определенный смысл в зависимости от его места в записи числа (от его позиции). Чаще всего применяют позиционную систему счисления с фиксированным основанием. Основанием системы может быть любое натуральное число ρ, ρ>1 Систематической записью натурального числа N по основанию ρ называют представление этого числа в виде суммы: N = аnρn+...+а1ρ, + а0 где аn, ..., а1, а0 - числа принимающие значения 0, 1, ..., ρ - 1, причем, аn≠0. Позиционная система счисления с основанием ρ называется ρ — ичной (двоичной, троичной и так далее). На практике чаще всего применяется десятичная ρ= 10). Для обозначения чисел 0, 1, ..., ρ - 1 в ρ - ичной системе счисления используют особые знаки, называемые цифрами. Древнеиндийские математики открыли нуль - особый знак, который должен был показать отсутствие единиц определенного разряда. Для ρ - ичной системы счисления нужно ρ цифр. Если ρ < 10, то применяются те же обозначения цифр, что и в десятичной системе счисления (только берутся цифры, меньше основания системы). В системах с основанием ρ > 10 для чисел, больших или равных 10, не вводят специальных символов, а используют десятичную запись этих чисел, заключая эту запись в скобки. Например, в четырнадцатеричной системе имеется четырнадцать цифр: 0, 1, 2, 3 ... 9, (10), (11), (12), (13). В системе счисления с основанием ρ, так же как и в десятичной системе счисления, место, занимаемое цифрой, считая, справа налево, называется разрядом. Число N= аnρ n+ . . . +a1ρ +а0 содержит а0 единиц первого разряда, а1 единиц второго разряда, а2 единиц третьего разряда и так далее. Единица следующего разряда в ρ раз больше единицы предыдущего разряда. Позиционные системы счисления удовлетворяют требованию возможности и однозначности записи любого натурального числа. Теорема. Любое натуральное число N может быть записано в системе с основание ρ и притом единственным образом. 6-7. НОД. Свойства НОДа. Алгоритм Евклида. НОК. Свойства НОКа. Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел. Обозначают НОД(a, b). Рассмотрим нахождения НОД на примере двух натуральных чисел 18 и 60: Разложим числа на простые множители: 18 = 2 × 3 × 3 60 = 2 × 2 × 3 × 5 Вычеркнуть из разложения первого числа все множители которые не входят в разложения второго числа, получим 2 × 3 Перемножаем оставшиеся простые множители после вычеркивания и получаем наибольший общий делитель чисел: НОД(18, 60)=2 × 3= 6. Заметим что не важно из первого или второго числа вычеркиваем множители, результат будет одинаков: 18 = 2 × 3 60 = 2 Второй способ нахождения наибольшего общего делителя с помощью алгоритма Евклида. Алгоритм Евклида является наиболее эффективным способом нахождения НОД, используя его нужно постоянно находить остаток от деления чисел и применять рекуррентную формулу. Рекуррентная формула для НОД, НОД(a, b)=НОД(b, a mod b), где a mod b - остаток от деления a на b. Найдем НОД(7920, 594) с помощью алгоритма Евклида, вычислять остаток от деления будем с помощью калькулятора. НОД(7920, 594) НОД(594, 7920 mod 594) = НОД(594, 198) НОД(198, 594 mod 198) = НОД(198, 0) НОД(198, 0) = 198 7920 mod 594 = 7920 - 13 × 594 = 198 594 mod 198 = 594 - 3 × 198 = 0 В результате получаем НОД(7920, 594) = 198 Наименьшим общим кратным натуральных чисел a и b называют наименьшее натурально число, которое кратно и a, и b. Обозначают НОК(a, b). Рассмотрим нахождения НОК на примере двух натуральных чисел 18 и 60: Разложим числа на простые множители: 18 = 2 × 3 × 3 60 = 2 × 2 × 3 × 5 Добавляем отсутствующие множители из разложения второго числа, получим 2 × 2 × 3 × 3 × 5. Перемножаем простые множители после добавления и получаем наименьшее общее кратное чисел: НОК(18, 60)=2 × 2 × 3 × 3 × 5= 180. Свойства наибольшего общего делителя НОД(a, b) = НОД(b, a) НОД(a, b) = НОД(-a, b) НОД(a, b) = НОД(|a|,|b|) НОД(a, 0) = |a| НОД(a, к • a) = |a|, при любом к ∈ Z НОД(a, НОД(b, с)) = НОД(НОД(a, b), c) Если d | a и d | b, то d | (a+b) и d | (a-b) Если d | a и d | b, то d | (ax+by) для любых целых x и y d | a - означает d делит без остатка a Свойства наименьшего общего кратного НОК(a, b) = НОК(b, a) НОД(a, b) = НОД(-a, b) НОД(a, b) = НОД(|a|,|b|) Н Отношение НОК и НОД: 3. Уравнения. Решения уравнения первой степени. Два числа или какие-нибудь выражения, соединенные знаком « = », образуют равенство. Если данные числа или выражения при любых значениях букв равны, то такое равенство называют тождеством. Например, когда утверждают, что при любом а действительном: а + 1 = 1 + а, здесь равенство является тождеством. Уравнением называется равенство, содержащее неизвестные числа, обозначенные буквами. Эти буквы называют неизвестными. Неизвестных в уравнении может быть несколько. Например, в уравнении 2х + у = 7х – 3 два неизвестных: х и у. Выражение, стоящее в уравнении слева (2х + у) называют левой частью уравнения, а выражение, стоящее в уравнении справа (7х – 3), называют правой его частью. Значение неизвестного, при котором уравнение становится тождеством, называется решением или корнем уравнения. Уравнения первой степени Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид Пример. 2х + 3 = 7 – 0,5х ; 0,3х = 0. У Пример. Решить уравнение . Р После сокращения получим: 4(х-4)+6(х+1)-12=30(х-3)+24х-2(11х+43). Раскроем скобки, чтобы отделить члены, содержащие неизвестное и свободные члены: 4х-16+6х+6-12=30х-90+24х-22х-86 Сгруппируем в одной части (левой) члены, содержащие неизвестное, а в другой части (правой) - свободные члены: 4х+6х-30х-24х+22х=-90-86+16-6+12 Приведем подобные члены: -22х=-154. Разделив обе части на (-22), получим х = 7. |
