Числовые системы
 Скачать 1.01 Mb.
|
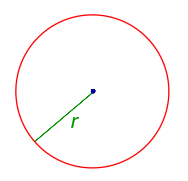
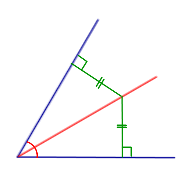
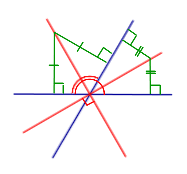
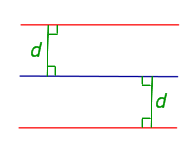
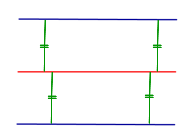
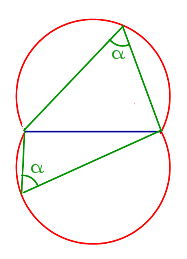
Средняя линия, какого-либо треугольника, всегда расположена параллельно одной из его сторон и является половиной этой стороны.32. Геометрические места точек. Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком. Другими словами, все точки из рассматриваемого геометрического места точек, и только они, удовлетворяют заданному условию. Примеры геометрических мест точек (сокращённо ГМТ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом. Геометрические места точек на плоскости
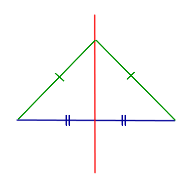
33. Центральная симметрия (симметрия относительно точки О) на плоскости. Теория: Симметрия— слово греческого происхождения, как и многие другие слова, которые связаны с математикой. Оно означает соразмерность, наличие определённого порядка, закономерности в расположении частей. Смотря на объекты вокруг, мы не раз восклицаем: «Какая симметрия!» Люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре, художестве, строительстве. Но симметрия широко распространена и в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, морской звезде. П 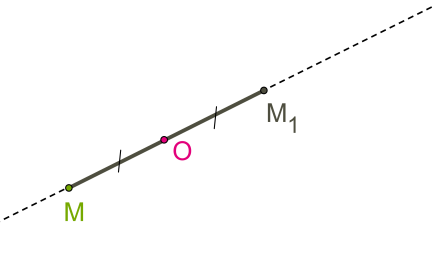 ока рассмотрим две симметрии на плоскости: относительно точки и прямой.Центральная симметрия. Симметрию относительно точки называютцентральной симметрией. Т 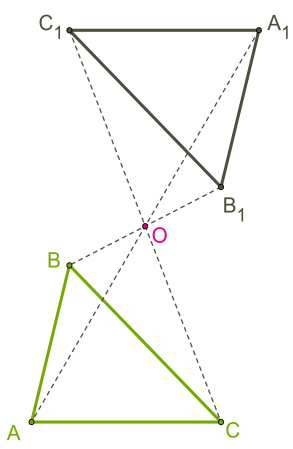 очки M и M1 симметричны относительно некоторой точки O, если точка O является серединой отрезка MM1.Точка O называется центром симметрии. Алгоритм построения центрально-симметричных фигур. Построим треугольник A1B1C1, симметричный треугольнику ABC, относительно центра (точки) O: 1. Для этого соединим точки A, B, C с центром O и продолжим эти отрезки; 2. Измерим отрезки AO, BO, COи отложим с другой стороны от точки O, равные им отрезки AO=OA1;BO=OB1;CO=OC1; 3. Соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику ABC. Определение. Фигуры, симметричные относительно некоторой точки, равны. Определение. Фигура симметрична относительно центра симметрии, если для каждой этой точки фигуры симметричная ей точка также лежит на этой фигуре. Такая фигура имеет центр симметрии (фигура с центральной симметрией). Есть фигуры с центральной симметрией — это, например, окружность и параллелограмм. У окружности центр симметрии — это её центр, у параллелограмма центр симметрии — это точка, в которой пересекаются его диагонали. Есть очень много фигур, у которых нет центра симметрии. 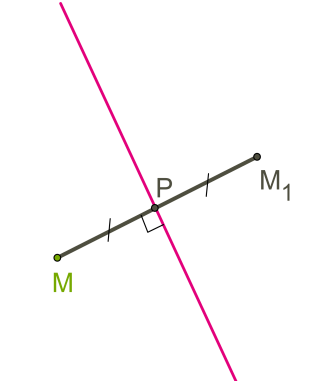 34.Осевая симметрия (симметрия относительно прямой 1) на плоскости. Осевая симметрия— это симметрия относительно проведённой прямой (оси). Определение. Точки M и M1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии. Алгоритм построения фигуры, симметричной относительно некоторой прямой. П 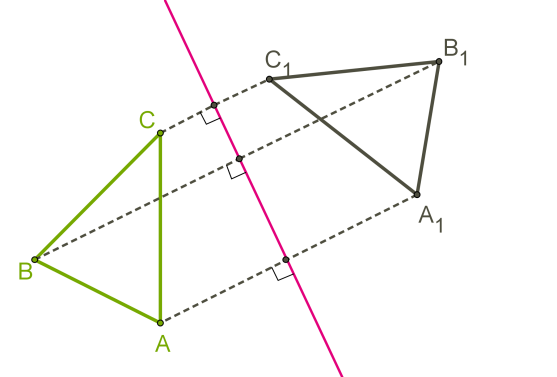 остроим треугольник A1B1C1, симметричный треугольнику ABC относительно красной прямой:1 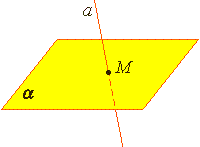 . Для этого проведём из вершин треугольника ABC прямые, перпендикулярные оси симметрии и продолжим их дальше на другой стороне оси.2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния. 3. Соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику ABC. Определение. Фигуры, симметричные относительно прямой, равны. О  пределение. Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры, симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.Иногда у фигур несколько осей симметрии: Для неразвёрнутого угла существует единственная ось симметрии — это биссектриса данного угла. Для равнобедренного треугольника есть единственная ось симметрии. Для равностороннего треугольника — три оси. Для прямоугольника и ромба существуют две оси симметрии. Д  ля квадрата — целых четыре.Для окружности осей симметрии бесчисленное множество — это каждая прямая, которая проходит через центр этой фигуры. Е 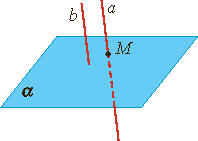 сть фигуры без осей симметрии — это параллелограмм и треугольник, все стороны которого различны.36.Основные понятия стереометрии. Аксиомы стереометрии. Стереометрия— это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять. Простейшие фигуры в пространстве: точка, прямая, плоскость. Плоскость. 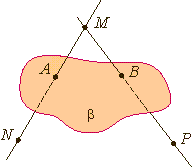  Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко  это записывают так: А ∈ β, B ∈ β,Аксиомы стереометрии и их следствия А   ксиома 1.Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.Аксиома 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую). И 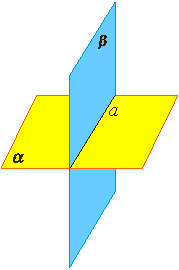 з аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.Аксиома 3. Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты |
