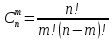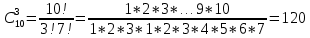42. Уравнение фигур на плоскости.
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру – значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде F(x,y) = 0 . Если выбрать на плоскости некоторую прямоугольную систему координат, то в ней уравнение называется уравнением фигуры Ф при выполнении следующих двух условий:
1. Если точка М(а,b) принадлежит фигуре Ф , то координаты (a,b) являются решениями уравнения F(x,y) = 0 , т.е. F(a,b) = 0 ;
2. если пара чисел (c,d) является решением уравнения F(x,y) = 0 , то точка N(c,d) принадлежит фигуре Ф .
Это определение в более компактной записи выглядит следующим образом. Уравнение F(x,y) = 0 . называется уравнением фигуры, если М(а,b) 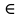 Ф Ф 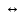 F(a,b) = 0 , то есть (a,b) – решение уравнения F(x,y) = 0 . . F(a,b) = 0 , то есть (a,b) – решение уравнения F(x,y) = 0 . .
Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения F(x,y) = 0 . , т.е. уравнение фигуры задает эту фигуру.
Возможны два вида задач:
1. дано уравнение F(x,y) = 0 . и надо построить фигуру Ф , уравнением которой является F(x,y) = 0 . ;
2. дана фигура Ф и надо найти уравнение этой фигуры.
П  ервая задача сводится к построению графика уравнения F(x,y) = 0 . и решается, чаще всего, методами математического анализа. ервая задача сводится к построению графика уравнения F(x,y) = 0 . и решается, чаще всего, методами математического анализа.
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
1. Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
2. Записать в координатах условие, сформулированное в первом пункте.
35. Подобие. Движение.
Подобие – это отображение плоскости на себя, которое не является движением.
Параллельный перенос Преобразование, при котором каждая точка фигуры перемещается в одном и том же направлении на одно и то же расстояние, называется параллельным переносом.
Подобие — преобразование евклидова пространства, при котором для любых двух точек A,В и их образов A', B' имеет место соотношение |A'B'|=k|AB|, где k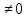 — коэффициент подобия. — коэффициент подобия.
Д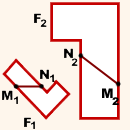 ля обозначения подобия используется значок ля обозначения подобия используется значок .
Подобные фигуры — это фигуры, для которых существует взаимно-однозначное соответствие, при котором расстояние между любыми парами их соответствующих точек изменяется в одно и то же число раз.
Н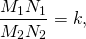 апример, то, что фигуры F1 м F2 подобны означает, что для любых двух точек M1 и N1 фигуры F1 и сопоставленных им точек M2 и N2 фигуры F2 выполняется соответствие апример, то, что фигуры F1 м F2 подобны означает, что для любых двух точек M1 и N1 фигуры F1 и сопоставленных им точек M2 и N2 фигуры F2 выполняется соответствие
где k — одно и тоже число для всех точек (k>0).
Число k называется коэффициентом подобия.
Преобразование фигуры F1 в фигуру F2, при котором расстояния между точками изменяется в одно и то же число раз, называется преобразованием подобия. При k=1 преобразование подобия является движением.
Движение — это отображение плоскости на себя, при котором сохраняются расстояния между точками.
См. 33-34 вопрос
31. Чертежные инструменты. Простейшие задачи на плоскости.
Готова́льня — набор чертёжных инструментов, заключённый в специальный футляр. В зависимости от назначения готовальни бывают универсальные (тип У), конструкторские (тип КБ и КМ), для копировочных работ (тип К) и для школьных работ (тип Ш).
В готовальню входят: циркуль, рейсфедер, чертёжный кронциркуль, разметочный кронциркуль, пропорциональный циркуль и другие инструменты.
Лине́йка — простейший измерительный инструмент, как правило представляющий собой узкую пластину, у которой как минимум одна сторона прямая. Обычно линейка имеет нанесённые штрихи (деления), кратные единице измерения длины (сантиметр, миллиметр, дюйм), которые используются для измерения расстояний. Линейки обычно производят из пластика или дерева, реже из металлов.
Транспорти́р (фр. transporteur, от лат. transporto «переношу») — инструмент для построения и измерения углов. Транспортир состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы), разделённого на градусы от 0 до 180°. В некоторых моделях — от 0 до 360°.
Угольник — чертёжный, слесарный, столярный инструмент для построения углов, обычно представляет собой прямоугольный треугольник с острыми углами 30° и 60° или по 45°. Является разновидностью линейки.
Ци́ркуль (от лат. circulus — круг, окружность) — инструмент для черчения окружностей и дуг окружностей, также может быть использован для измерения расстояний, в частности, на картах. Может быть использован в геометрии, черчении, для навигации и других целей.
24. Строение курса геометрии.
Геометрия — это наука о свойствах геометрических фигург треугольника, квадрата, круга, пирамиды, сферы и др.
Слово «геометрия» греческое, в переводе на русский язык означает «землемерие».
Геометрия, которая изучается в школе, называется евклидовой по нмени древнегреческого ученого Евклида, жившего в III в. до н. э.
Школьная геометрия состоит из двух частей: планиметрии и стереометрии.
П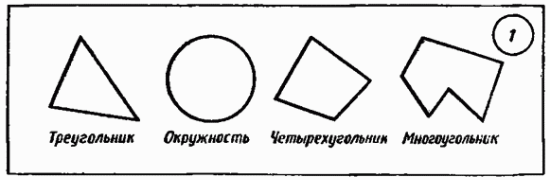 ланиметрия — это раздел геометрии, в котором изучаются геометрические фигуры на плоскости. Стереометрия — это раздел геометрии, в котором изучаются фигуры в пространстве. ланиметрия — это раздел геометрии, в котором изучаются геометрические фигуры на плоскости. Стереометрия — это раздел геометрии, в котором изучаются фигуры в пространстве.
На рисунке 1 изображены различные фигуры на плоскости. Всякую геометрическую фигуру мы представляем себе составленной из точек. Часть любой геометрической фигуры также является геометрической фигурой.
21-22. Неравенство. Область определения неравенства. Способы решений неравенств.
Неравенством называется запись, в которой функции соединены знаком (или несколькими знаками) отношения ">", "<", "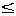 ", " ", "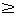 ". ".
Неравенства, содержащие два знака отношения, называются двойными, три знака отношения — тройными и т.п. Примеры таких неравенств:
f(x) > g(x),
f(x) < g(x),
f(x)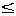 g(x), g(x),
f(x)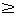 g(x). g(x).
f(x) < h(x) < g(x) это пример двойного неравенства.
Неравенства f(x) > g(x), f(x) < g(x), называются строгими, а неравенства
f(x)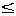 g(x), f(x) g(x), f(x)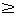 g(x) — нестрогими. g(x) — нестрогими.
Решением неравенства, называется всякое значение переменой, при котором данное неравенство верно. Например, решением неравенства f(x) > g(x) является всякое значение переменной x = a, при котором справедливо неравенство
f(a) > g(a), или функция f(x) при x = a принимает большее значение чем функция g(x).
Областью определения (областью допустимых значений) неравенства 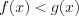 называют общую часть областей определения функций называют общую часть областей определения функций 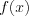 и и 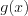
Задание "решить неравенство" означает, что требуется найти множество всех его решений. Это множество может оказаться пустым — в случае, когда решений нет. Множество всех решений неравенства будем называть его ответом.
Неравенство В называется следствием неравенства А, если всякое решение А является решением неравенства В. В этом случае используется запись А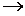 В. Два неравенства А иВ называются равносильными (или эквивалентными пишем В. Два неравенства А иВ называются равносильными (или эквивалентными пишем
А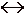 В либо А В либо А
В), если их ответы совпадают. Если А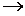 В и В В и В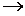 А, то неравенства А и В эквивалентны. А, то неравенства А и В эквивалентны.
Запись нескольких неравенств под знаком фигурной скобки называется системой (число и вид неравенств, входящих в систему, может быть произвольным). Решение системы неравенств есть пересечение решений всех входящих в нее неравенств. Двойное неравенство f(x) < g(x) < h(x) можно записать в виде системы:
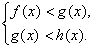 Запись нескольких неравенств, объединенных квадратной скобкой, называется совокупностью данных неравенств. Решение совокупности есть объединение решений входящих в нее неравенств. Запись нескольких неравенств, объединенных квадратной скобкой, называется совокупностью данных неравенств. Решение совокупности есть объединение решений входящих в нее неравенств.
Основные правила, применяемые при решении неравенств
Если какое-либо слагаемое перенести из одной части неравенства в другую, изменив при этом его знак на противоположный, то получим неравенство, равносильное данному.
Если обе части неравенства умножить (разделить) на одно и то же положительное число, то получим неравенство, равносильное данному.
Если обе части неравенства умножить (разделить) на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получим неравенство, равносильное данному.
В зависимости от того, какие функции входят в неравенство, различают линейные, квадратные, дробно-рациональные, иррациональные, логарифмические, показательные неравенства, неравенства с параметром.
Если требуется все общие решения двух или нескольких неравенств, то решают систему неравенств. Как и систему уравнений, систему неравенств записывают с помощью фигурной скобки. Решение системы неравенств есть пересечение решений всех входящих в нее неравенств.
20. Уравнение. Способы решения уравнений.
Уравнение — это математическое равенство с одной или несколькими неизвестными величинами, например 2х+3у=0.
Выражения по обе стороны знака равенства называются левой и правой частями уравнения. Буквами латинского алфавита обозначаются неизвестные. Хотя число неизвестных может быть любым. Числа, на которые умножается неизвестная, называются коэффициентами.
При переносе члена уравнения из одной части в другую его знак меняется на противоположный: плюс меняется на минус и наоборот.
Обе части уравнения можно умножать и делить на число, не равное нулю.
Введение новой переменой
17-18. Элементарные функции. Неэлементарные функции.
О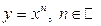 сновными элементарными функциями называются следующие аналитическим способом заданные функции. сновными элементарными функциями называются следующие аналитическим способом заданные функции.
I. Степеннйя функция , где n — действительное число.
II. Показательная функция: , где а — положительное число, не равное единице.
I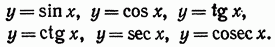 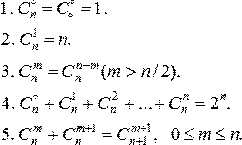 II. Логарифмическая функция: , где основание логарифмов а — положительное число, не равное единице. II. Логарифмическая функция: , где основание логарифмов а — положительное число, не равное единице.
IV. Тригонометрически функции:
V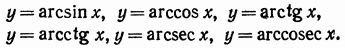 . Обратные тригонометрические функции: . Обратные тригонометрические функции:
Элементарной функцией называется функция, которая записывается одной формулой вида 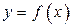 , где справа стоящее выражение , где справа стоящее выражение 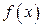 составлено из основных элементарных функций и чисел при помощи конечного числа операций сложения, вычитания, умножения, деления и суперпозиции функций. составлено из основных элементарных функций и чисел при помощи конечного числа операций сложения, вычитания, умножения, деления и суперпозиции функций.
Неэлементарной функцией называется функция, которая не относится к элементарным; например, если она не записывается одной формулой или содержит бесконечное число арифметических операций.
Например, неэлементарными являются следующие функции:
1) 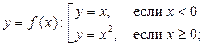
2) функция Дирихле: 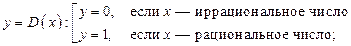
3) 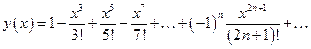 . .
15-16. Комбинаторика. Определение перестановки. Размещения и сочетания. Формула связи числа размещений, перестановки и сочетаний.
Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее употребительные из них.
Перестановками называются комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок Pn=n! где n!=1*2*2..n. Иногда удобно рассматривать 0!, полагая по определению, 0!=1.
Пример 1.Менеджер ежедневно просматривает 6 изданий экономического содержания. Если порядок просмотра случаен, то сколько существует способов его осуществления?
Способы просмотра изданий различаются только порядком, так как число, а значит, и состав изданий при каждом способе неизменны. Следовательно, при решении этой задачи необходимо вычислить число перестановок: Pn=6!=1*2*3*4*5*6=720
Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений. 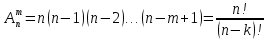
Пример 2. Правление банка выбирает из 10 кандидатов 3 человека на различные должности (все 10 кандидатов имеют равные шансы). Сколько всевозможных групп по 3 человека можно составить из 10 кандидатов?
Необходимо рассчитать число комбинаций из 10 элементов по 3. Так как группы по 3 человека могут отличаться и составом претендентов, и заполняемыми ими вакансиями (они все разные), т. е. порядком, то для ответа необходимо вычислить число размещений из 10 элементов по 3: 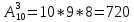 . Можно составить 720 групп. . Можно составить 720 групп.
Сочетаниями называются комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементов. Число сочетаний 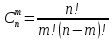
Свойства сочетаний
Пример 3.Правление банка выбирает из 10 кандидатов 3 человека на одинаковые должности (все 10 кандидатов имеют равные шансы). Сколько всевозможных групп по 3 человека можно составить из 10 кандидатов?
Состав различных групп должен отличаться по крайней мере хотя бы одним кандидатом и порядок выбора кандидата не имеет значения (все вакансии одинаковы), следовательно, этот вид комбинаций представляет собой сочетания 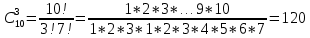
Можно составить 120 групп из 10 человек по 3.
Следует различать сочетания от размещений. Например, если в группе 20 студентов и 7 человек из них, выйдя из аудитории на перерыв, стоят вместе и беседуют, то порядок, в котором они стоят, не существенен. Число всех возможных групп из 20 человек по 7 в данном случае – сочетания. Если же студенты отправились на перерыве в буфет или в кассу за стипендией, то тогда существенно, в каком порядке они стали, т. е. кто из них первый, кто второй и т. д. В этой ситуации при подсчете возможных групп из 20 человек по 7 необходимо составлять размещения.
Отметим, что числа перестановок, размещений и сочетаний связаны равенством
П 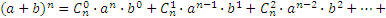 ри решении задач комбинаторики используют следующие правила: ри решении задач комбинаторики используют следующие правила:
П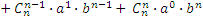 равило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m+n способами. равило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m+n способами.
Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m*n способами.
|
 Скачать 1.01 Mb.
Скачать 1.01 Mb. Ф
Ф 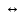 F(a,b) = 0 , то есть (a,b) – решение уравнения F(x,y) = 0 . .
F(a,b) = 0 , то есть (a,b) – решение уравнения F(x,y) = 0 . .
 ервая задача сводится к построению графика уравнения F(x,y) = 0 . и решается, чаще всего, методами математического анализа.
ервая задача сводится к построению графика уравнения F(x,y) = 0 . и решается, чаще всего, методами математического анализа.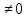 — коэффициент подобия.
— коэффициент подобия. ля обозначения подобия используется значок
ля обозначения подобия используется значок 
 ланиметрия — это раздел геометрии, в котором изучаются геометрические фигуры на плоскости. Стереометрия — это раздел геометрии, в котором изучаются фигуры в пространстве.
ланиметрия — это раздел геометрии, в котором изучаются геометрические фигуры на плоскости. Стереометрия — это раздел геометрии, в котором изучаются фигуры в пространстве.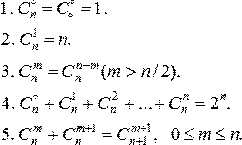 II. Логарифмическая функция: , где основание логарифмов а — положительное число, не равное единице.
II. Логарифмическая функция: , где основание логарифмов а — положительное число, не равное единице.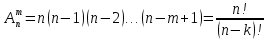
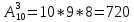 . Можно составить 720 групп.
. Можно составить 720 групп.