Цифровые устройства. Что такое цифровые микросхемы. Виды цифровых микросхем
 Скачать 2.25 Mb. Скачать 2.25 Mb.
|
Глава 10Цифроаналоговые преобразователи R-2RЦифроаналоговый преобразователь с взвешиванием токов прост для понимания принципов работы, однако обладает рядом недостатков. Первый из них — это требование к высокой точности изготовления резисторов. Если разброс тока старшего разряда окажется больше значения тока младшего разряда, то ЦАП не будет выполнять свою функцию. Второй недостаток связан с влиянием паразитных емкостей схемы. При больших разрядностях ЦАП с взвешиванием токов приходится применять высокоомные резисторы. Это приводит к большому времени заряда и разряда паразитной емкости микросхемы, что ограничивает ее быстродействие. Ну и, наконец, сами резисторы. Высокоомные резисторы занимают огромную площадь на кристалле микросхемы. Все эти недостатки привели к поиску другого схемотехнического решения цифроаналогового преобразователя. Таким решением стало применение матрицы R-2R. Принцип формирования опорных напряжений матрицей R-2R приведен на рисунке 10.1. 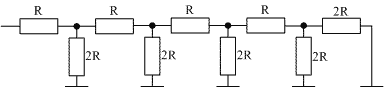 Рисунок 10.1. Матрица резисторов R-2R В матрице резисторов R-2R формируется ряд напряжений, отличающихся друг от друга ровно в два раза. Рассмотрим этот механизм. В конце резистивной цепочки находятся два резистора с сопротивлением 2R. Эти резисторы одним концом соединены друг с другом, другие концы присоединены к корпусу схемы, то есть резисторы соединены параллельно. В результате их общее сопротивление равно R. При соединении резистора R и параллельного соединения двух резисторов 2R образуется делитель напряжения с коэффициентом деления 2. В результате напряжение на его выходе будет в два раза меньше напряжения на его входе. Общее сопротивление делителя составляет 2R, так как сопротивления R в нем соединены последовательно. В результате в следующем звене матрицы ситуация повторяется. Снова образуется параллельное соединение двух резисторов 2R и снова образуется делитель напряжения в два раза. Так как напряжения в узлах матрицыR-2R отличаются друг от друга ровно в два раза, то и ток через резисторы 2R будет отличаться ровно в два раза, то есть подчиняться двоичному закону. Если теперь эти токи подавать или не подавать на вход сумматора токов в зависимости от входного двоичного числа, то мы получим цифроаналоговый преобразователь. Схема подобного цифроаналогового преобразователя с применением матрицы R-2R приведена на рисунке 10.2. 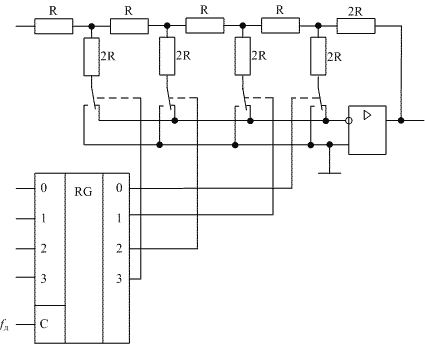 Рисунок 10.2. Принципиальная схема четырехразрядного цифро-аналогового преобразователя R-2R Раздел 11 Микросхемы цифровой обработки сигналов 11.1 Основные блоки цифровой обработки сигналов Глава 1 Двоичные сумматоры Построение двоичных сумматоров обычно начинается с сумматора по модулю 2. На рисунке 11.1.1 приведена таблица истинности этого сумматора. Ее можно получить исходя из правил суммирования в двоичной арифметике. Предполагается, что читатель знаком с основами двоичной арифметики. Более подробно операции над двоичными числами будут рассмотрены позднее. Рисунок 11.1.1 Таблица истинности сумматора по модулю 2 В соответствии с принципами построения произвольной таблицы истинности, рассмотренными в предыдущей главе, получим схему сумматора по модулю 2. Эта схема приведена на рисунке 11.1.2 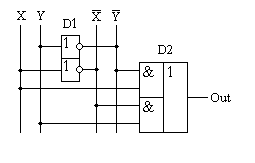 Рисунок 11.1.2 Принципиальная схема сумматора по модулю 2 Сумматор по модулю 2 (для двоичной арифметики его схема совпадает со схемой исключающего "ИЛИ") изображается на схемах как показано на рисунке 11.1.3 Рисунок 11.1.3 Условно-графическое изображение схемы исключающего "ИЛИ" Сумматор по модулю 2 выполняет суммирование без учета переноса. В полном двоичном сумматоре требуется учитывать перенос, поэтому требуются схемы, позволяющие формировать перенос в следующий двоичный разряд. Таблица истинности такой схемы, называемой полусумматором, приведена на рисунке 11.1.4 Рисунок 11.1.4 Таблица истинности полусумматора В соответствии с принципами построения произвольной таблицы истинности получим схему полусумматора. Эта схема приведена на рисунке 11.1.5. 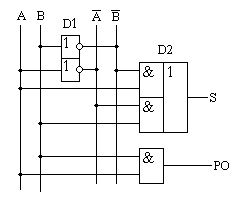 Рисунок 11.1.5. Принципиальная схема, реализующая таблицу истинности полусумматора. Полусумматор изображается на схемах как показано на рисунке 11.1.6. Рисунок 11.1.6 Изображение полусумматора на схемах. Схема полусумматора формирует перенос в следующий разряд, но не может учитывать перенос из предыдущего разряда, поэтому она и называется полусумматором. Таблицу истинности полного двоичного одноразрядного сумматора можно получить из правил суммирования двоичных чисел. Она приведена на рисунке 11.1.7. В обозначении входов использовано следующее правило: в качестве входов использованы одноразрядные числа A и B; перенос обозначен буквой P; для обозначения входа переноса используется буква I (сокращение от английского слова input – вход); для обозначения выхода переноса используется буква O (сокращение от английского слова output – выход). Рисунок 11.1.7 Таблица истинности полного двоичного одноразрядного сумматора. В соответствии с принципами построения принципиальной схемы по произвольной таблице истинностиполучим схему полного двоичного одноразрядного сумматора. Эта схема приведена на рисунке 11.1.8 Ее можно минимизировать, но это несколько усложняет принципы построения сумматоров, поэтому вопросы минимизации рассматриваться не будут. 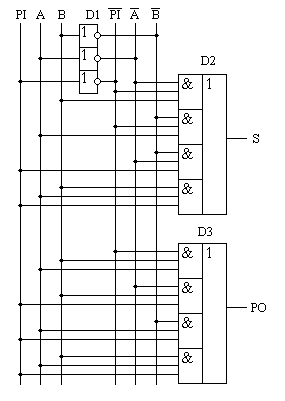 Рисунок 11.1.8 Принципиальная схема, реализующая таблицу истинности полного двоичного одноразрядного сумматора. Полный двоичный одноразрядный сумматор изображается на схемах как показано на рисунке 11.1.9 Рисунок 11.1.9 Условно-графическое изображение полного двоичного одноразрядного сумматора Для того чтобы получить многоразрядный сумматор, достаточно соединить входы и выходы переносов соответствующих двоичных разрядов. Схема соединения одноразрядных сумматоров для реализации четырехразрядного сумматора приведена на рисунке 11.1.10 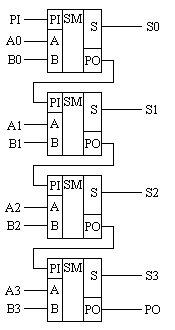 Рисунок 11.1.10 Принципиальная схема многоразрядного двоичного сумматора Одноразрядные сумматоры практически никогда не использовались, так как почти сразу же были выпущены микросхемы многоразрядных сумматоров. Полный двоичный четырехразрядный сумматор изображается на схемах как показано на рисунке 11.1.11 Рисунок 11.1.11 Условно-графическое изображение полного двоичного многоразрядного сумматора Естественно, в приведенной на рисунке 11.1.10 схеме рассматриваются только принципы работы двоичных сумматоров. В реальных схемах никогда не допускают последовательного распространения переноса через все разряды многоразрядного сумматора. Для увеличения скорости работы двоичного сумматора применяется отдельная схема формирования переносов для каждого двоичного разряда. Таблицу истинности для такой схемы легко получить из алгоритма суммирования двоичных чисел, а затем применить хорошо известные нам принципы построения цифровой схемы по произвольной таблице истинности. На этом пока закончим рассмотрение принципов работы сумматора, более сложные операции будут рассмотрены позднее, а пока для дальнейшего понимания работы операционного блока процессора необходимо научиться переключать двоичные числа на входах и выходе сумматора. Это позволяют сделать мультиплексоры и демультиплексоры, основной частью которых является дешифратор, поэтому следующим устройством, которое мы рассмотрим, будет декодер. Дешифратор является частным случаем декодер Глава 2 Умножители Умножение в двоичном виде производится подобно умножению в десятичной системе счисления. Как мы это помним из школьного курса, легче всего осуществлять умножение в столбик. При этом потребуется перемножить каждый разряд множимого на соответствующий разряд множителя, а затем просуммировать полученные частные произведения. Рассмотрим в качестве примера умножение двух четырёхразрядных двоичных чисел. Пусть требуется умножить число 10112 (1110) на число 11012 (1310). Мы в результате умножения ожидаем получить число 100011112(14310). Выполним операцию умножения в столбик, как это показано на рисунке 11.12 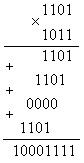 Рисунок 11.1.12 Выполнение операции умножения в столбик Для формирования произведения требуется вычислить четыре частичных произведения. Обратите внимание, что в двоичной арифметике требуется выполнять умножение только на числа 0 и 1. Это означает, что нужно либо суммировать множимое к сумме остальных частичных произведений, либо нет. Таким образом, для формирования частичного произведения можно воспользоваться логическими элементами "2И". Для формирования частичного произведения, кроме операции умножения на один разряд, требуется осуществлять его сдвиг влево на число разрядов, соответствующее весу разряда множителя. Сдвиг можно осуществить простым соединением соответствующих разрядов частичных произведений к необходимым разрядам двоичного сумматора. Для того чтобы принципиальная схема умножителя была похожа на алгоритм двоичного умножения, приведённый на рисунке 11.1.12, используем условно-графические изображения микросхем, где входы расположены сверху, а выходы снизу. В полном соответствии с алгоритмом умножения в столбик нам потребуются тричетырёхразрядных сумматора. Принципиальная схема умножителя, реализующая алгоритм двоичного умножения в столбик, приведена на рисунке 11.1.13. Формирование частичных произведений в этой схеме осуществляют микросхемы D1, D3, D5, D7. В этих микросхемах содержится сразу четыре логических элемента "2И". Сумматор, выполненный на микросхеме D6, суммирует первое и второе частные произведения. При этом младший разряд первого частного произведения не нуждается в суммировании (см. рисунок 11.1.12). Поэтому он подаётся на выход умножителя непосредственно (разряд M0). Второе частное произведение должно быть сдвинуто на один разряд. Это осуществляется тем, что младший разряд выходного числа сумматора D6 соединяется со вторым разрядом произведения (M1). Но тогда первое частное произведение необходимо сдвинуть на один разряд по отношению ко второму частному произведению! Это выполняется тем, что младший разряд группы входов A соединяется с первым разрядом частного произведения, первый разряд группы входов A соединяется со вторым разрядом частного произведения, и т.д. Однако старший разряд группы входов A не с чем соединять! Вспомним, что если добавить к числу слева ноль, то значение числа не изменится, поэтому мы можем этот разряд соединить с общим проводом схемы. Точно таким же образом осуществляется суммирование третьего и четвёртого частного произведения. Это суммирование выполняют микросхемы D4 и D2 соответственно. Отличие заключается только в том, что здесь не нужно задумываться о старшем разряде предыдущей суммы, ведь предыдущая микросхема сумматора формирует сигнал переноса. 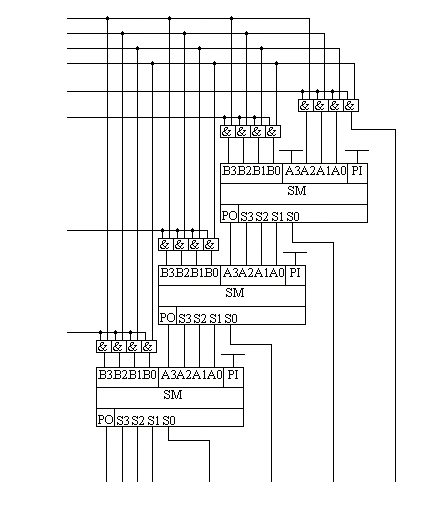 Рисунок 11.1.13 Схема матричного умножителя 4*4 Если внимательно посмотреть на схему умножителя, то можно увидеть, что она образует матрицу, сформированную проводниками, по которым передаются разряды числа A и числа B. В точках пересечения этих проводников находятся логические элементы “2И”. Именно по этой причине умножители, реализованные по данной схеме, получили название матричных умножителей. Скорость работы схемы, приведенной на рисунке 11.1.13, определяется максимальным временем распространения сигнала. Это цепь D7, D6, D4, D2. Время работы схемы можно сократить, если сумматоры располагать не последовательно друг за другом, как это предполагается алгоритмом, приведенным на рис. 11.1.12, а суммировать частичные произведения попарно, затем суммировать пары частичных произведений и т.д. В этом случае время выполнения операции умножения значительно сократится. Особенно заметен выигрыш в быстродействии при построении многоразрядных умножителей, однако ничего не бывает бесплатно. В обмен на быстродействие придётся заплатить увеличением разрядности сумматоров, а значит сложностью схемы. Если сумматоры частных произведений останутся той же разрядности, что и ранее, то разрядность сумматоров пар частичных произведений должна быть увеличена на единицу. Разрядность сумматоров четвёрок частичных произведений будет на два разряда больше разрядности сумматоров частичных произведений и т.д. Глава 3 Постоянные запоминающие устройства. Очень часто в различных применениях требуется хранение информации, которая не изменяется в процессе эксплуатации устройства. Это такая информация как программы в микроконтроллерах, начальные загрузчики (BIOS) в компьютерах, таблицы коэффициентов цифровых фильтров в сигнальных процессорах, DDC и DUC, таблицы синусов и косинусов в NCO и DDS. Практически всегда эта информация не требуется одновременно, поэтому простейшие устройства для запоминания постоянной информации (ПЗУ) можно построить на мультиплексорах. Иногда в переводной литературе постоянные запоминающие устройства называются ROM (read only memory — память доступная только для чтения). Схема такого постоянного запоминающего устройства (ПЗУ) приведена на рисунке 11.1.14 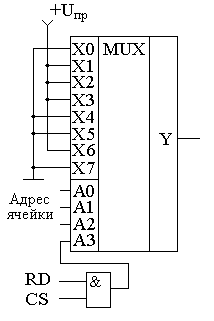 Рисунок 11.1.14 Схема постоянного запоминающего устройства (ПЗУ), построенная на мультиплексоре. В этой схеме построено постоянное запоминающее устройство на восемь одноразрядных ячеек. Запоминание конкретного бита в одноразрядную ячейку производится запайкой провода к источнику питания (запись единицы) или запайкой провода к корпусу (запись нуля). На принципиальных схемах такое устройство обозначается как показано на рисунке 11.1.15 Рисунок 11.1.15 Обозначение постоянного запоминающего устройства на принципиальных схемах. Для того, чтобы увеличить разрядность ячейки памяти ПЗУ эти микросхемы можно соединять параллельно (выходы и записанная информация естественно остаются независимыми). Схема параллельного соединения одноразрядных ПЗУ приведена на рисунке 11.1.16 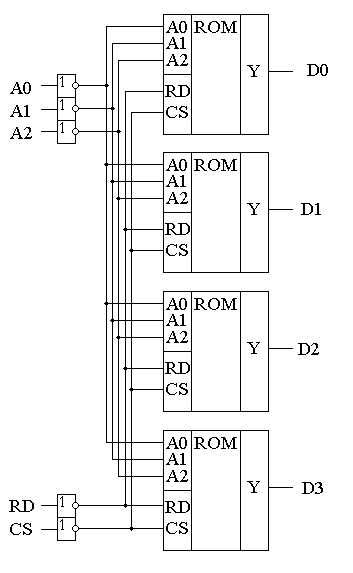 Рисунок 11.1.16 Схема многоразрядного ПЗУ (ROM). В реальных ПЗУ запись информации производится при помощи последней операции производства микросхемы — металлизации. Металлизация производится при помощи маски, поэтому такие ПЗУ получили название масочных ПЗУ. Еще одно отличие реальных микросхем от упрощенной модели, приведенной выше — это использование кроме мультиплексора еще и демультиплексора. Такое решение позволяет превратить одномерную запоминающую структуру в двухмерную и, тем самым, существенно сократить объем схемы дешифратора, необходимого для работы схемы ПЗУ. Эта ситуация иллюстрируется следующим рисунком: 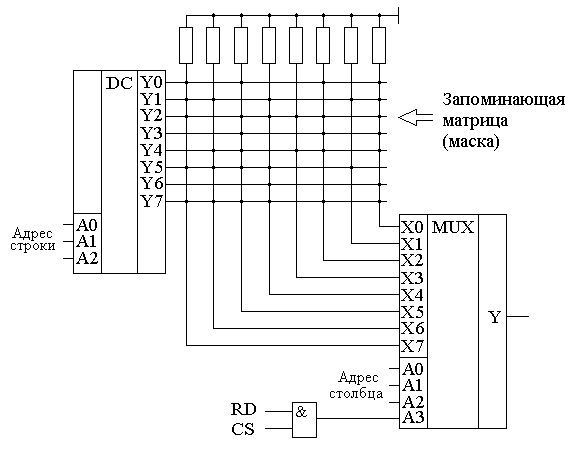 Рисунок 11.1.17 Схема масочного постоянного запоминающего устройства (ROM). Масочные ПЗУ изображаются на принципиальных схемах как показано на рисунке 11.1.18 Адреса ячеек памяти в этой микросхеме подаются на выводы A0 ... A9. Микросхема выбирается сигналом CS. При помощи этого сигнала можно наращивать объем ПЗУ (пример использования сигнала CS приведён при обсуждении ОЗУ). Чтение микросхемы производится сигналом RD. 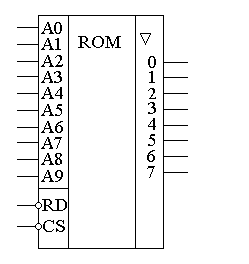 Рисунок 11.1.18 Условно-графическое обозначение масочного ПЗУ (ROM) на принципиальных схемах. Программирование масочного ПЗУ производится на заводе изготовителе, что очень неудобно для мелких и средних серий производства, не говоря уже о стадии разработки устройства. Естественно, что для крупносерийного производства масочные ПЗУ являются самым дешевым видом ПЗУ, и поэтому широко применяются в настоящее время. Для мелких и средних серий производства радиоаппаратуры были разработаны микросхемы, которые можно программировать в специальных устройствах — программаторах. В этих ПЗУ постоянное соединение проводников в запоминающей матрице заменяется плавкими перемычками, изготовленными из поликристаллического кремния. При производстве ПЗУ изготавливаются все перемычки, что эквивалентно записи во все ячейки памяти ПЗУ логических единиц. В процессе программирования ПЗУ на выводы питания и выходы микросхемы подаётся повышенное питание. При этом, если на выход ПЗУ подаётся напряжение питания (логическая единица), то через перемычку ток протекать не будет и перемычка останется неповрежденной. Если же на выход ПЗУ подать низкий уровень напряжения (присоединить к корпусу), то через перемычку запоминающей матрицы будет протекать ток, который испарит ее и при последующем считывании информации из этой ячейки ПЗУ будет считываться логический ноль. Такие микросхемы называются программируемыми ПЗУ (ППЗУ) или PROM и изображаются на принципиальных схемах как показано на рисунке 11.1.19. В качестве примера ППЗУ можно назвать микросхемы 155РЕ3, 556РТ4, 556РТ8 и другие. 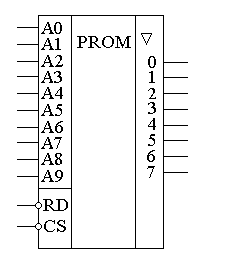 Рисунок 11.1.19 Условно-графическое обозначение программируемого постоянного запоминающего устройства (PROM) на принципиальных схемах. Программируемые ПЗУ оказались очень удобны при мелкосерийном и среднесерийном производстве. Однако при разработке радиоэлектронных устройств часто приходится менять записываемую в ПЗУ программу. ППЗУ при этом невозможно использовать повторно, поэтому раз записанное ПЗУ при ошибочной или промежуточной программе приходится выкидывать, что естественно повышает стоимость разработки аппаратуры. Для устранения этого недостатка был разработан еще один вид ПЗУ, который мог бы стираться и программироваться заново. ПЗУ с ультрафиолетовым стиранием строится на основе запоминающей матрицы построенной на ячейках памяти, внутреннее устройство которой приведено на следующем рисунке: 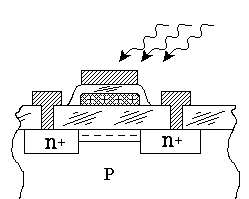 Рисунок 11.1.20 Запоминающая ячейка ПЗУ с ультрафиолетовым и электрическим стиранием. Ячейка представляет собой МОП транзистор, в котором затвор выполняется из поликристаллического кремния. Затем в процессе изготовления микросхемы этот затвор окисляется и в результате он будет окружен оксидом кремния — диэлектриком с прекрасными изолирующими свойствами. В описанной ячейке при полностью стертом ПЗУ, заряда в плавающем затворе нет, и поэтому транзистор ток не проводит. При программировании ПЗУ, на второй затвор, находящийся над плавающим затвором, подаётся высокое напряжение и в плавающий затвор за счет туннельного эффекта индуцируются заряды. После снятия программирующего напряжения индуцированный заряд остаётся на плавающем затворе, и, следовательно, транзистор остаётся в проводящем состоянии. Заряд на плавающем затворе подобной ячейки может храниться десятки лет. Структурная схема описанного постоянного запоминающего устройства не отличается от описанного ранее масочного ПЗУ. Единственное отличие — вместо плавкой перемычки используется описанная выше ячейка. Такой вид ПЗУ называется репрограммируемыми постоянными запоминающими устройствами (РПЗУ) или EPROM. В РПЗУ стирание ранее записанной информации осуществляется ультрафиолетовым излучением. Для того, чтобы этот свет мог беспрепятственно проходить к полупроводниковому кристаллу, в корпус микросхемы ПЗУ встраивается окошко из кварцевого стекла. При облучении микросхемы РПЗУ, изолирующие свойства оксида кремния теряются, накопленный заряд из плавающего затвора стекает в объем полупроводника, и транзистор запоминающей ячейки переходит в закрытое состояние. Время стирания микросхемы РПЗУ колеблется в пределах 10 — 30 минут. Количество циклов записи — стирания микросхем EPROM находится в диапазоне от 10 до 100 раз, после чего микросхема РПЗУ выходит из строя. Это связано с разрушающим воздействием ультрафиолетового излучения на оксид кремния. В качестве примера микросхем EPROM можно назвать микросхемы 573 серии российского производства, микросхемы серий 27сXXX зарубежного производства. В РПЗУ чаще всего хранятся программы BIOS универсальных компьютеров. РПЗУ изображаются на принципиальных схемах как показано на рисунке 11.1.21 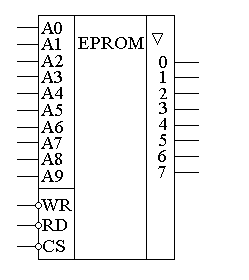 Рисунок 11.1.21 Условно-графическое обозначение РПЗУ (EPROM) на принципиальных схемах. Так так корпуса с кварцевым окошком очень дороги, а также малое количество циклов записи-стирания привели к поиску способов стирания информации из РПЗУ электрическим способом. На этом пути встретилось много трудностей, которые к настоящему времени практически решены. Сейчас достаточно широко распространены микросхемы с электрическим стиранием информации. В качестве запоминающей ячейки в них используются такие же ячейки как и в РПЗУ, но они стираются электрическим потенциалом, поэтому количество циклов записи-стирания для этих микросхем достигает 1000000 раз. Время стирания ячейки памяти в таких ПЗУ уменьшается до 10 мс. Схема управления для электрически стираемых программируемых ПЗУ получилась сложная, поэтому наметилось два направления развития этих микросхем:
Электрически стираемые ППЗУ (EEPROM) дороже и меньше по объему, но зато позволяют перезаписывать каждую ячейку памяти отдельно. В результате эти микросхемы обладают максимальным количеством циклов записи-стирания. Область применения электрически стираемых ПЗУ — хранение данных, которые не должны стираться при выключении питания. К таким микросхемам относятся отечественные микросхемы 573РР3, 558РР3 и зарубежные микросхемы EEPROM серии 28cXX. Электрически стираемые ПЗУ обозначаются на принципиальных схемах как показано на рисунке 11.1.22. 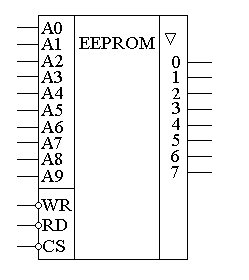 Рисунок 11.1.22 Условно-графическое обозначение электрически стираемого постоянного запоминающего устройства (EEPROM) на принципиальных схемах. В последнее время наметилась тенденция уменьшения габаритов ЭСППЗУ за счет уменьшения количества внешних выводов микросхем. Для этого адрес и данные передаются в микросхему и из микросхемы через последовательный порт. При этом используются два вида последовательных портов — SPI порт и I2C порт (микросхемы 93сXX и 24cXX серий соответственно). Зарубежной серии 24cXX соответствует отечественная серия микросхем 558РРX. FLASH-ПЗУ отличаются от ЭСППЗУ тем, что стирание производится не каждой ячейки отдельно, а всей микросхемы в целом или блока запоминающей матрицы этой микросхемы, как это делалось в РПЗУ.  Рисунок 11.1.23 Условно-графическое обозначение FLASH памяти на принципиальных схемах. При обращении к постоянному запоминающему устройству сначала необходимо выставить адрес ячейки памяти на шине адреса, а затем произвести операцию чтения из микросхемы. Эта временная диаграмма приведена на рисунке 11.1.24 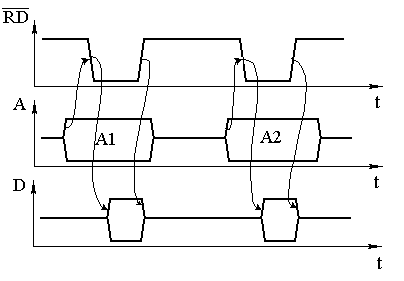 Рисунок 11.1.24 Временные диаграммы сигналов чтения информации из ПЗУ. На рисунке 11.1.24 стрелочками показана последовательность, в которой должны формироваться управляющие сигналы. На этом рисунке RD — это сигнал чтения, A — сигналы выбора адреса ячейки (так как отдельные биты в шине адреса могут принимать разные значения, то показаны пути перехода как в единичное, так и в нулевое состояние), D — выходная информация, считанная из выбранной ячейки ПЗУ. Глава 4 Цифровые фильтры. Прежде чем начать подробное обсуждение вопросов реализации цифровых фильтров давайте вспомним - что же такое частотные фильтры? Частотные фильтры требуются для подавления нежелательных сигналов, отличающихся от полезного по частоте. В частотной области зависимость коэффициента передачи фильтра можно изобразить так, как это приведено на рисунке 11.1.25 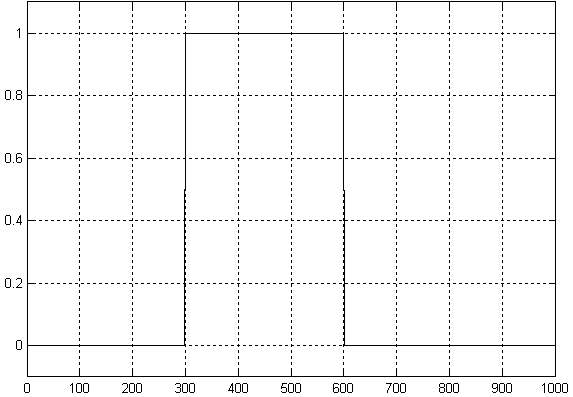 Рисунок 11.1.25 Идеализированная амплитудно-частотная характеристика коэффициента передачи фильтра. На этом рисунке приведена частотная характеристика фильтра, выделяющего нужную нам полосу частот. Однако мы знаем, что операция фильтрации (выделения полезной части данных) в частотной области эквивалентна операции вычисления свёртки во временной области и наоборот: 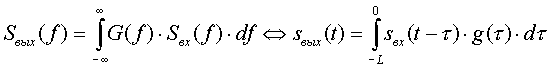 где S(f) - спектр сигнала s(t) - временная реализация сигнала G(f) - частотная характеристика полосового фильтра g(t) - импульсная характеристика полосового фильтра L - длина импульсной характеристики полосового фильтра Таким образом, для реализации фильтра нам достаточно определить форму импульсной характеристики фильтра и вычислить операцию свертки. Импульсная характеристика связана с частотной характеристикой преобразованием Фурье. Поэтому в простейшем случае рассчитать цифровой фильтр можно, используя преобразование Фурье от требуемой частотной характеристики. Кроме формы импульсной характеристики для создания цифрового фильтра нам требуется уметь запоминать значения входного сигнала в предыдущие моменты времени. Для этого могут быть использованы параллельные регистры, внутреннее устройство которых рассмотрено в предыдущих главах. В формуле вычисления свертки используется арифметическая операция умножения. Устройство, способное выполнять эту операцию мы тоже уже рассматривали ранее. Остается только операция интегрирования. Однако при использовании целочисленных значений входного сигнала ее можно представить как сумму всех отсчетов этого сигнала, а внутреннее устройство арифметического сумматора мы тоже уже знаем. Рассмотрим структурную схему устройства, способного вычислять операцию свёртки (цифровой фильтр). Эта схема приведена на рисунке11.1.26. 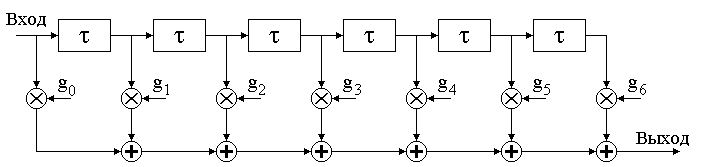 Рисунок 11.1.26. Структурная схема устройства, способного вычислять операцию свёртки. Давайте проверим, как будет реагировать это устройство на одиночный импульс единичной амплитуды, поданный на его вход. Для наглядности рассуждений возьмем импульсную характеристику одиночного колебательного контура. Эта характеристика приведена на рисунке 11.1.27. 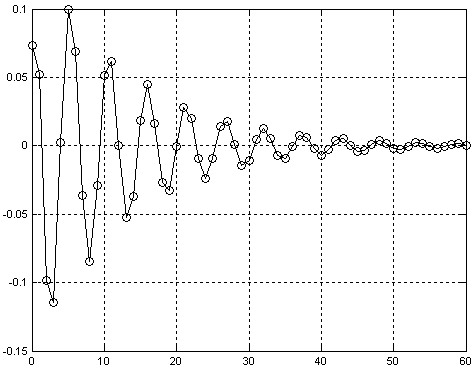 Рисунок 11.1.27 Форма импульсной характеристики колебательного контура. На рисунке кружочками обозначены значения весовых коэффициентов импульсной характеристики цифрового фильтра. Именно эти коэффициенты подаются на входы умножителей в схеме, приведенной на рисунке 11.1.26. Для наглядности эти коэффициенты соединены между собой прямыми линиями (так характеристика становится более похожей на импульсную характеристику аналогового колебательного контура). Частотная характеристика фильтра, обладающего импульсной характеристикой, соответствующей рисунке 11.1.27, приведена на рисунке 11.1.28. По оси абсцисс на этом рисунке приведена частота в кГц, а по оси ординат - коэффициент передачи фильтра в дБ. 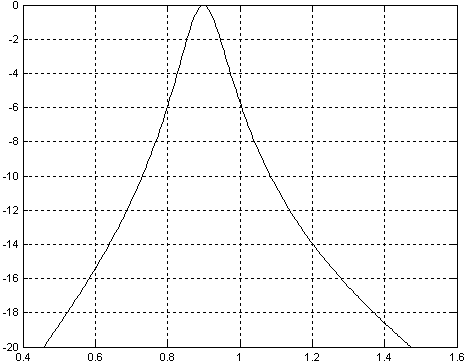 Рисунок 11.1.28. Форма частотной характеристики фильтра. Теперь подадим на вход схемы, приведенной на рисунке 11.1.26, цифровой код, соответствующий единичному уровню сигнала. В первый момент времени во всех внутренних регистрах фильтра содержатся нулевые значения. Это означает, что при умножении этих значений на весовые коэффициенты мы получим в результате нули. Отличаться будет только результат на выходе первого умножителя. При перемножении весового коэффициента g0 на единичное значение входного сигнала мы получим на выходе умножителя значение сигнала с амплитудой g0. Как мы уже знаем, задержка в схеме определяется частотой тактового сигнала, подаваемого на входы синхронизации параллельных регистров. При поступлении первого тактового импульса код, присутствовавший на входе схемы, запишется в первый регистр (элемент задержки). По этому же сигналу содержимое первого регистра (нулевое значение) перепишется во второй регистр, содержимое второго регистра перепишется в третий регистр и т.д. Как мы договорились, теперь на вход фильтра мы подадим код, соответствующий нулевому значению сигнала. В результате снова на выходе всех умножителей, кроме второго умножителя, будет присутствовать нулевой код. Так как в первом регистре на этот раз содержится единичное значение, то в результате умножения на коэффициент g1, на выходе второго умножителя мы получим значение сигнала с амплитудой g1. При поступлении последующих тактовых импульсов процесс будет повторяться, и мы на выходе схемы последовательно будем получать значения сигналов, соответствующие весовым коэффициентам. Итак, мы убедились, что схема ведёт себя подобно обычному фильтру, и научились рассчитывать весовые коэффициенты этой схемы, требуемые для получения заданных характеристик фильтров. Собственно говоря, было бы удивительно не получить фильтр, ведь обычные аналоговые схемы фактически работают так же. Энергия на колебательном контуре постепенно накапливается за счет суммирования текущего входного напряжения и всех предыдущих значений, активный RC фильтр с обратными связями ведет себя точно так же. Преимуществом рассмотренной схемы является то, что в ней мы можем выбирать коэффициенты импульсной характеристики произвольным образом без ограничений, которые обычно существуют в других видах фильтров. В результате мы можем получить исключительные свойства, нереализуемые в других схемах. Например, мы можем получить строго симметричную импульсную характеристику фильтра, подав на умножители коэффициенты, соответствующие этой импульсной характеристике. Таким образом, как это известно из теории фильтров, можно реализовать фильтр со строго линейной фазовой характеристикой. Это свойство чрезвычайно полезно для аппаратуры передачи данных или обработки телевизионных сигналов. В качестве еще одного примера использования рассмотренной ранее схемы можно назвать реализацию фильтров Найквиста. Как известно, в этих фильтрах импульсная характеристика должна принимать нулевые значения строго через определенные интервалы, равные длительности передаваемого символа. И это нам доступно - кто же может запретить нам записать в нужные ячейки памяти код нуля? 11.2 Микросхемы прямого цифрового синтеза радиосигналов. Глава 5 Фазовые аккумуляторы Для формирования синусоидального радиосигнала в цифровом виде можно воспользоваться ПЗУ с записанными в него значениями функции синуса. При считывании из него этих значений через равномерные промежутки времени, на выходе цифро-аналогового преобразователя можно наблюдать синусоидальный сигнал. Пример подобной формы сигнала приведен на рисунке 11.2.1 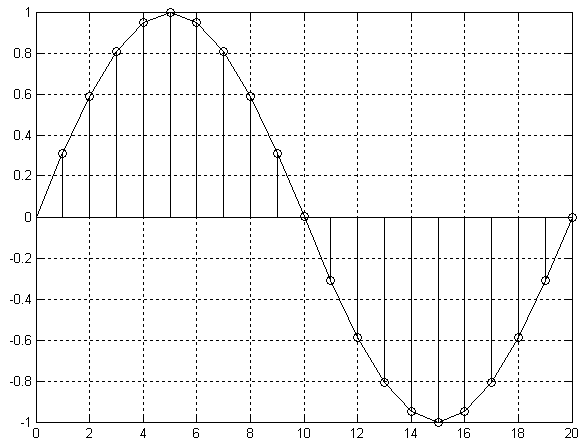 Рисунок 11.2.1 Временная диаграмма сигнала на выходе фазового аккумулятора. На этом рисунке кружочками обозначены значения напряжения на выходе цифро-аналогового преобразователя. По оси абсцисс отложен номер отсчета цифрового сигнала. Цифровое значение отсчета сигнала считывается из ячейки ПЗУ. Фильтр низкой частоты позволяет сгладить дискретность сигнала на выходе цифро-аналогового преобразователя. На рисунке 1 этот сигнал показан сплошной линией, соединяющей дискретные отсчеты сигнала. Как видно из приведенного рисунка, значение сигнала на выходе фазового аккумулятора в каждый момент времени определяется номером отсчета сигнала. Частоту полученного синусоидального сигнала можно изменять несколькими способами. Первый и наиболее очевидный способ заключается в изменении тактовой частоты устройства прямого цифрового синтеза. Однако такой способ изменения частоты выходного сигнала неудобен, так как приводит к необходимости применять в качестве тактового генератора синтезатор частот. Известно, что стабильность частоты колебания, вырабатываемого синтезатором, зависит от диапазона его перестройки. Еще одним очень существенным недостатком приведенного способа изменения частоты формируемого сигнала является то, что синтезатор частот не может мгновенно изменить свою частоту. Некоторое время после изменения частоты настройки синтезатора он будет колебаться около нового значения тактовой частоты. Второй способ перестройки частоты заключается в том, что при поступлении очередного тактового импульса можно считывать значения синусоидального сигнала из постоянного запоминающего устройства через одну или несколько ячеек. Если мы будем считывать значения синусоидального сигнала через одну ячейку памяти, то полностью период синусоидального сигнала на выходе аналого-цифрового преобразователя будет получен за время в два раза меньшее относительно первоначально рассмотренного случая. В результате частота формируемого синусоидального сигнала увеличится вдвое. Если мы будем выдавать на выход содержимое каждой третьей ячейки ПЗУ синусоидального сигнала, то для завершения периода этого сигнала нам потребуется втрое меньшее количество тактов, а значит, период формируемого сигнала будет в три раза короче первоначального случая. Итак, получается, что мы можем регулировать частоту выходного синусоидального сигнала, просто изменяя коэффициент счета входных импульсов. При этом номер отсчета синусоидального сигнала можно считать его фазой, а так как номер отсчета постоянно увеличивается, то устройство, осуществляющее это действие, можно назвать аккумулятором (накопителем) фазы. Фазовый аккумулятор можно выполнить на арифметическом сумматоре и регистре, запоминающем результат суммирования. На один из входов сумматора подадим содержимое накапливающего регистра, а на другой вход будем подавать шаг изменения фазы. Схема фазового аккумулятора приведена на рисунке 11.2.2 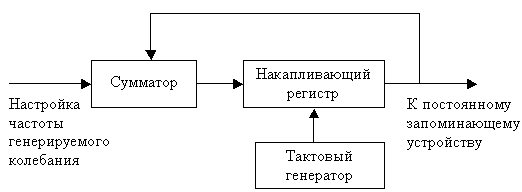 Рисунок 11.2.2 Структурная схема фазового аккумулятора Если на вход фазового аккумулятора будем подавать единицу, то эта схема будет работать как обычныйдвоичный счетчик. При подаче на вход этой схемы двойки числа на выходе накапливающего регистра будут изменяться через два. При подаче на вход числа пять, при поступлении очередного тактового импульса, содержимое аккумулятора будет изменяться на пять единиц. Даже если на вход фазового аккумулятора подадим число ноль, то мы получим нулевое приращение фазы, то есть нулевую частоту (постоянный ток). Таким способом можно регулировать частоту синусоидального сигнала, формируемого на выходе фазового аккумулятора. Теперь определим требования к параметрам блоков, входящих в состав фазового аккумулятора. Сначала определим количество ячеек постоянного запоминающего устройства. Количество ячеек будет определять минимальную частоту, которую мы сможем сформировать фазовым аккумулятором. Чем больше количество ячеек, тем ниже эта частота и соответственно меньше шаг перестройки синусоидального генератора. Пусть тактовая частота фазового аккумулятора будет 40 МГц. Тогда если выбрать количество ячеек ПЗУ равным 4096, то мы сможем получить минимальную частоту 10 кГц. Современные ПЗУ при приемлемой стоимости могут достигать объема 65536 ячеек. При использовании для хранения функции синуса таких ПЗУточность настройки частоты возрастет до 610 Гц. Теперь оценим необходимую разрядность ячеек постоянного запоминающего устройства. Для этого определим разность между значениями синуса, хранящимися в соседних ячейках памяти: D = sin(2×p/4069) – sin(0) = sin(2×p/4069) = 1,53×10–3 Эта разность соответствует точности одиннадцатиразрядного числа, которое обеспечивает точность представления чисел 0,98×10–3. Это означает, что для хранения значений синусов в постоянном запоминающем устройстве с 4096 ячейками памяти достаточно одиннадцати- двенадцатиразрядной точности. Для хранения синуса в ПЗУ с 65536 ячейками памяти потребуются уже шестнадцатиразрядные ячейки. Теперь определим требования к разрядности накапливающего регистра и сумматора. На первый взгляд разрядность этих устройств должна совпадать с разрядностью шины адреса постоянного запоминающего устройства. Однако это не так. При использовании для хранения синуса постоянного запоминающего устройства с шестнадцатиразрядными ячейками можно реализовать динамический диапазон устройства прямого цифрового синтеза до 96 дБ (по 6 дБ на каждый разряд). Это значительно превышает динамический диапазон аналоговых устройств. Поэтому увеличивать разрядность ячеек ПЗУ синуса не имеет смысла. Точно так же не имеет смысла увеличивать количество ячеек в этом ПЗУ. Кто сомневается, может провести расчеты по приведенной выше методике. Какой смысл хранить в соседних ячейках одинаковые значения?! Так что же, мы не можем получить шаг перестройки синусоидального генератора, реализованного на фазовом аккумуляторе, меньший рассчитанного выше значения? Да нет же, можем. Для этого достаточно увеличить разрядность сумматора и накапливающего регистра, а на адресные входы ПЗУ подавать старшие разряды результата суммирования, как это показано на рисунке 11.2.3. 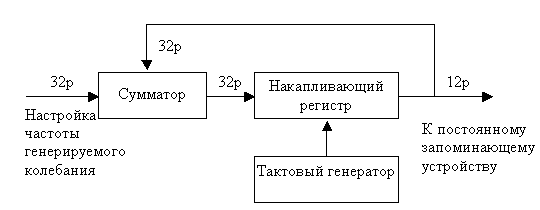 Рисунок 11.2.3. Принципиальная схема фазового аккумулятора В результате применения сумматора с разрядностью, большей разрядности адресной шины постоянного запоминающего устройства, в накапливающем регистре фаза может изменяться с любым сколь угодно малым шагом. При этом двоичный код напряжения на выходе ПЗУ будет изменяться только тогда, когда изменение значения синуса превысит шаг квантования цифро-аналогового преобразователя. При использовании шага изменения фазы, меньшего разрядности адресной шины ПЗУ, возможно дробное соотношение периода синуса и периода накопления фазы, равной 360° (переполнения фазового аккумулятора). В этом случае возможно формирование синусоидального сигнала с периодом, отличающимся в соседних интервалах времени. Однако средняя частота генерируемого синусоидального сигнала будет точно равна заданному значению. |
