Цифровые устройства. Что такое цифровые микросхемы. Виды цифровых микросхем
 Скачать 2.25 Mb. Скачать 2.25 Mb.
|
|
Глава 6 Полярные модуляторы Итак, мы научились управлять фазой и частотой синусоидального сигнала. Это означает, что мы можем осуществить частотную и фазовую модуляцию сигнала. Однако в ряде случаев требуется уметь управлять амплитудой синусоидального сигнала. Например, такое действие требуется при амплитудной модуляции. Рассмотрим формулу, описывающую синусоидальный сигнал: Анализируя эту формулу, мы видим, что для изменения амплитуды синусоидального сигнала достаточно умножить его на функцию, зависящую от времени. Строить цифровые умножители мы уже научились в предыдущих главах, поэтому, для того, чтобы получить амплитудный модулятор, достаточно в структурную схему устройства прямого цифрового синтеза просто добавить цифровой умножитель, как это показано на рисунке 11.2.4  Рисунок 11.2.4 Схема полярного модулятора В схеме, приведенной на рисунке 11.2.4, после постоянного запоминающего устройства и после умножителяпоставлены регистры. Они служат для увеличения быстродействия устройства в целом. Период тактовой частоты зависит от времени распространения сигнала по цифровым комбинационным схемам, таким каксумматор, умножитель или дешифраторы адреса постоянного запоминающее устройства. Время распространения через каждое из перечисленных устройств меньше времени распространения через все эти устройства сразу, поэтому введение дополнительных регистров позволяет увеличить тактовую частоту схемы прямого цифрового синтеза. Рассмотренная схема позволяет независимо изменять частоту и фазу генерируемого сигнала. Именно так представляется синусоидальный сигнал в полярной системе координат. Именно поэтому приведенная схема прямого цифрового синтеза сигнала получила название полярного модулятора. Глава 7 Квадратурные модуляторы. Полярные модуляторы позволяют легко реализовать аналоговые виды модуляции, такие как частотная, фазовая или амплитудная модуляции. Из цифровых методов модуляции полярные модуляторы позволяют осуществить MSK и GMSK модуляции. Реализация же таких видов модуляции как квадратурная амплитудная модуляция (КАМ) или фазовая модуляция с высокой скоростью передачи бит осуществляется легче при использовании квадратурного модулятора. Для осуществления квадратурной амплитудной модуляции потребуются два канала: синфазный канал I и квадратурный канал Q. На выходе модулятора сигналы с выходов умножителей суммируются. Для осуществления сдвига фаз в квадратурных каналах в ПЗУ можно записать сразу таблицу синуса и косинуса. Структурная схема квадратурного модулятора приведена на рисунке 11.2.5 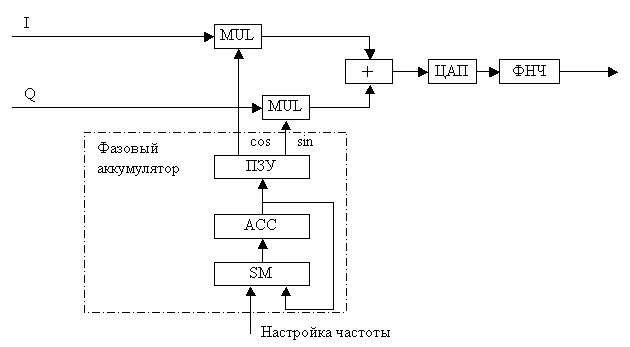 Рисунок 11.2.5 Структурная схема квадратурного модулятора В этой схеме квадратурные компоненты сигнала I и Q, подаваемые на вход умножителей должны быть сформированы в полосе частот от 0 до fв. В этой схеме также как и в схеме полярного модулятора должны быть промежуточные регистры, увеличивающие быстродействие всей схемы в целом, однако для увеличения наглядности рисунка они не показаны. В большинстве случаев тактовая частота квадратурных компонент сигнала не совпадает с тактовой частотой, необходимой для формирования высокочастотного сигнала. Для увеличения частоты отсчетов квадратурных сигналов обычно применяются интерполирующие фильтры. Давайте рассмотрим принципы работы этих фильтров подробнее. Глава 8 Интерполирующие цифровые фильтры. Интерполяцией называется увеличение количества отсчетов сигнала в единицу времени. Отношение количества новых отсчетов сигнала в единицу времени по отношению к предыдущему количеству отсчетов сигнала называется коэффициентом интерполяции. Обычно это отношение выбирается целым числом. При увеличении частоты отсчетов сигнала в соответствии с теоремой Котельникова расширяется полоса частот, описываемых этими отсчетами. Это означает, что в новую полосу частот попадает несколько частотных образов первоначального варианта сигнала. При интерполяции необходимо выбрать нужный частотный образ. Обычно выбирается полоса частот от 0 до fв. Задача выбора необходимого частотного образа решается при помощи цифрового фильтра. Такой фильтр называется интерполирующим. Именно этот фильтр вычисляет значения сигнала в точках между первоначальными отсчетами сигнала. Рассмотрим пример первоначального представления сигнала во временной области. Пример временной реализации сигнала приведен на рисунке 11.2.6 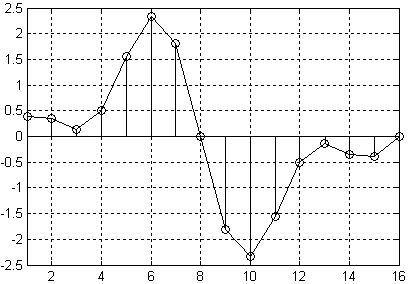 Рисунок 11.2.6 Пример временной реализации сигнала. На данном рисунке отсчеты сигнала обозначены кружочками, а для того чтобы легче было видеть форму сигнала, они соединены прямыми линиями. При интерполяции сигнала требуется увеличить количество его отсчетов в единицу времени. Новые отсчеты сигнала заполняются нулевыми значениями, как это показано на рисунке 11.2.7 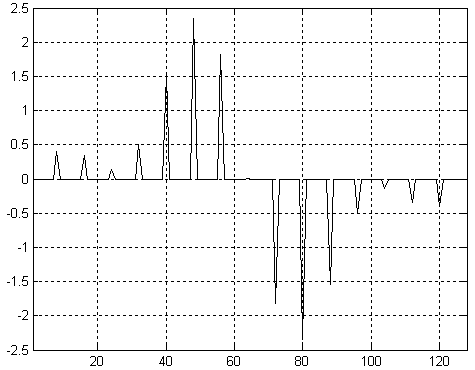 Рисунок 11.2.7 Сигнал на входе интерполирующего фильтра. Спектр этого же сигнала приведен на рисунке 11.2.8. На графике четко виден повторяющийся характер спектра. Теперь для того, чтобы осуществить интерполяцию сигнала необходимо подавить нежелательные спектральные компоненты сигнала. 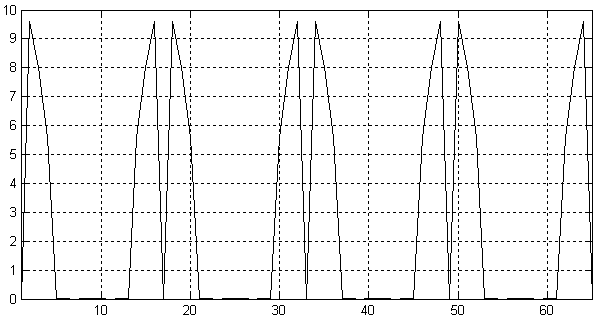 Рисунок 11.2.8. Спектр сигнала, приведенного на рисунке 11.2.7. Подавим все высокочастотные составляющие спектра сигнала при помощи цифрового фильтра. Для этого зададимся уровнем подавления этих составляющих спектра –75 дБ. Такие параметры можно реализовать цифровым фильтром со 128 отводами. Получившаяся амплитудно-частотная характеристика интерполирующего КИХ-фильтра, структурная схема которого рассматривалась нами ранее (рисунок 11.2.7), c шестнадцатиразрядными коэффициентами. 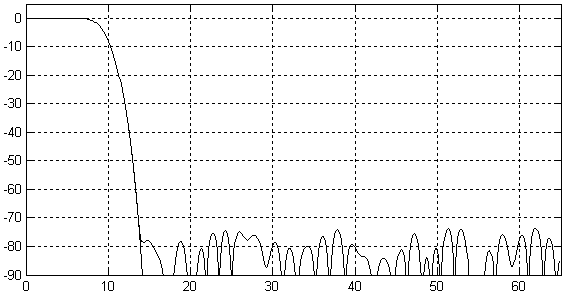 Рисунок 11.2.9 Амплитудно-частотная характеристика интерполирующего фильтра. В полосе пропускания такой фильтр обеспечивает неравномерность коэффициента передачи на уровне 0,001 дБ. Таким образом, учитывая, что фильтр с конечной импульсной характеристикой обладает линейной фазовой характеристикой, он практически не вносит искажений в исходный сигнал. При прохождении через разработанный фильтр сигнал принимает вид, приведенный на рисунке 11.2.10 Сигнал на выходе фильтра будет задержан на групповое время задержки фильтра. Для КИХ-фильтра это время равно тактовой частоте умноженной на половину количества отводов фильтра. На рисунке 11.2.10 приведено 128 временных отсчетов сигнала. Они практически сливаются друг с другом, поэтому отдельные отсчеты не выделяются кружочками, как это было сделано на рисунке 11.2.6. Как видно из приведенного на рисунке графика сигнал на выходе фильтра практически не отличается от исходного (существовавшего до дискретизации) сигнала. 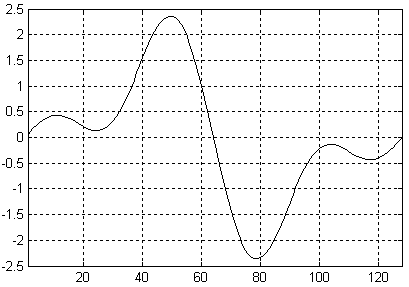 Рисунок 11.2.10 Сигнал на выходе интерполирующего фильтра. Так как реальный фильтр всегда имеет конечную крутизну ската своей амплитудно-частотной характеристики, то полоса частот сигнала, подлежащего интерполяции всегда должна быть меньше половины частоты дискретизации. Только в этом случае интерполяция сигнала может быть выполнена без искажений. Теперь рассмотрим, как будет выглядеть этот же сигнал, если выделить первый образ исходного сигнала. Получившийся сигнал приведен на рисунке 11.2.11. Так как в этом случае номера отсчетов сигнала не нормированы относительно начала координат, то на этом же рисунке приведен низкочастотный образ сигнала. 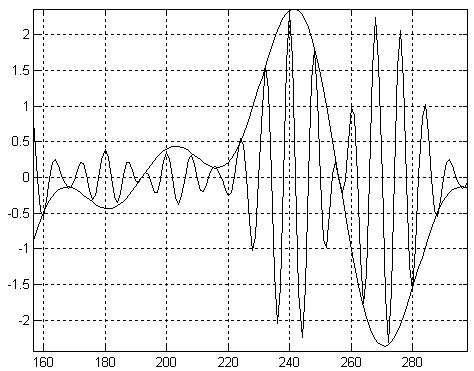 Рисунок 11.2.11 Сигнал на выходе интерполирующего фильтра. На рисунке отчетливо видно, что исходные значения сигнала совпадают как в низкочастотном, так и в первом образе сигнала. В момент пересечения нулевого значения фаза несущей частоты первого образа меняет свой знак. Точно так же вели бы себя и второй и третий образ сигнала. Отличие заключается только в значении несущей частоты. Применение для формирования несущей частоты высокочастотных образов первоначального сигнала неудобно, так как в этом случае можно реализовать всего несколько фиксированных частот. Намного удобнее для переноса спектра исходного сигнала на несущую частоту использовать схему квадратурного модулятора. Эта схема позволяет переносить спектр исходного сигнала на любую частоту, не превышающую половину частоты дискретизации. Интерполяция обычно производится в несколько этапов. Первые два этапа обычно обеспечивают увеличение скорости отсчетов сигнала в два раза каждый. Это связано с тем, что первоначально почти вся полоса частот от 0 до fд/2 занята полезным сигналом, т.е. полезный сигнал и его высокочастотные образы находятся близко друг от друга. В результате от интерполирующего фильтра требуется высокая крутизна ската амплитудно-частотной характеристики и для его реализации требуется большое количество отводов и коэффициентов. После выполнения этих первых двух этапов интерполяции полезный сигнал занимает только 25% полосы частот. В результате требования к избирательности фильтра уменьшаются, а значит, последующий интерполирующий фильтр может обеспечить больший коэффициент интерполяции. Здесь я хотел бы подчеркнуть, что промежуточные отсчеты должны быть заполнены именно нулями. Если их заполнить другими значениями, например повторениями предыдущего отсчета сигнала, то уровень высокочастотных составляющих спектра значительно уменьшится. Однако при этом будет искажен и сигнал в основной полосе. Более того, станет невозможным применять в качестве фильтра-интерполятора фильтры Найквиста, так как исходные значения отсчетов сигнала будут искажены. В заключение я хотел бы привести структурную схему прямого синтеза, на вход которой можно подавать цифровой поток с частотой отсчетов, в несколько раз ниже по отношению к требующейся для формирования выходного радиосигнала. Эта схема приведена на рисунке 11.2.12.  Рисунок 11.2.12. Структурная схема квадратурного модулятора с низкоскоростным потоком квадратурных сигналов. Глава 9 Однородные интерполирующие цифровые фильтры. Наиболее просто в цифровом виде реализовать рассмотренный нами ранее однородный фильтр, так как для его реализации не требуются цифровые умножители. Для однородного фильтра седьмого порядка формула выглядит следующим образом:
Структурная схема фильтра, реализующего формулу 1, приведена на рисунке 11.2.13  Рисунок 11.2.13 Структурная схема однородного фильтра седьмого порядка При реализации такого фильтра потребуется 6 сумматоров. Во столько же раз уменьшится быстродействие цифрового фильтра. Можно несколько видоизменить структуру данного фильтра. Для сокращения количества выполняемых операций формула 3.3 может быть переписана в следующем виде:
Эта формула может быть реализована за два действия:
В таком случае для реализации однородного фильтра потребуется два каскада. Второй каскад будет выполнять интегрирование, а первый — фильтр с конечной импульсной характеристикой всего с двумя ненулевыми коэффициентами, равными единице. Новая структурная схема однородного фильтра приведена на рисунке 11.2.14. 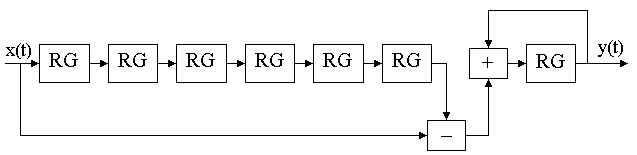 Рисунок 11.2.14 Структурная схема двухкаскадного фильтра, эквивалентного фильтру, приведенному на рисунке 11.2.13 В этой схеме максимальное время задержки сигнала определяется быстродействием сумматора и временем записи в регистр. Мы увеличили быстродействие схемы почти в семь раз. Ну а теперь вспомним, что анализируемый фильтр работает при частоте дискретизации сигнала в N раз выше частоты дискретизации входного сигнала. В этом случае для формирования того же самого значения времени задержки до увеличения частоты дискретизации нам потребуется всего только один регистр, так как на его вход тактовой синхронизации будет поступать частота, в шесть раз меньше, чем частота синхронизации на выходе интерполирующего фильтра. Это означает, что имеет смысл тактировать первую часть фильтра входной частотой дискретизации. Получившаяся в результате всех описанных выше преобразований структурная схема однородного фильтра-интерполятора приведена на рисунке 11.2.15.  Рисунок 11.2.15. Структурная схема фильтра-интерполятора, эквивалентного фильтру, приведенному на рисунке 11.2.14 Новая схема содержит всего два регистра и два двоичных сумматора, то есть данная схема получилась в три раза проще схемы однородного фильтра, приведенной на рисунке 11.2.14. Получившийся в результате преобразований фильтр трудно назвать однородным, однако для того, чтобы отобразить особенности его импульсной и амплитудно-частотной характеристик, сохраним название "однородный" и для этого фильтра. В иностранной литературе такой фильтр получил название CIC-фильтр. Если по техническому заданию требуется еще больший коэффициент интерполяции по сравнению с рассмотренным выше случаем, то выигрыш при реализации однородного фильтра-интерполятора по схеме, приведенной на рисунке 11.2.15, будет еще большим. Хотелось бы напомнить, что при анализе характеристик однородного фильтра для получения приемлемого уровня подавления мешающего сигнала нам потребовалось включить друг за другом несколько каскадов. Давайте включим последовательно друг за другом три фильтра-интерполятора, как это показано на структурной схеме фильтра, приведенной на рисунке 11.2.16. 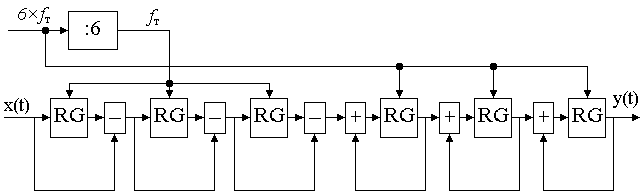 Рисунок 11.2.16. Структурная схема трехкаскадного фильтра-интерполятора (CIC3) Приведена амплитудно-частотная характеристика четырехкаскадного однородного фильтра. Обратите внимание, что образ полезного сигнала сосредоточен около частоты дискретизации исходного сигнала x(t). Проанализировав амплитудно-частотную характеристику четырехкаскадного однородного фильтра можно определить, что этот фильтр в полосе частот высокочастотных образов полезного сигнала может обеспечить подавление мешающих сигналов до 90 дБ, что эквивалентно 16-разрядному представлению полезного сигнала. На приведенном рисунке черным цветом закрашена область частот, которая подавляется однородным интерполирующим фильтром. Остальные частоты (там, где находятся максимумы в полосе подавления однородного фильтра) были подавлены ранее полуполосными интерполирующими фильтрами.  Рисунок 11.2.17. Амплитудно-частотная характеристика четырехкаскадного однородного фильтра-интерполятора На этом закончим обзор особенностей реализации интерполирующих цифровых фильтров.
Глава 10 Квадратурные демодуляторы. В цифровых приемниках перенос частоты осуществляется сразу на нулевую частоту. При приеме сигналов со сложными видами модуляции важен точный прием не только амплитудной, но и фазовой составляющей сигнала. Для того чтобы не потерять фазу принимаемого сигнала, из сигнала с выхода цифрового фильтра основной избирательности выделяется его синфазная I и квадратурная составляющие. Для этого сигнал умножается на тригонометрические функции sin(wпрt) и cos(wпрt). На выходе умножителя на синусоидальную функцию формируется сигнал, описываемый следующей формулой:  После пропускания этого сигнала через цифровой фильтр низкой частоты на его выходе остается сигнал квадратурной составляющей входного сигнала. На выходе умножителя на косинусоидальную функцию формируется сигнал, описываемый следующей формулой: 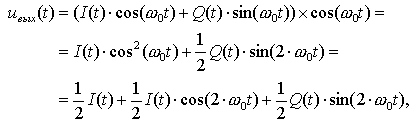 Этот сигнал тоже пропускается через фильтр низких частот с точно такой же частотной характеристикой. На выходе этого фильтра остается сигнал синфазной составляющей входного сигнала. Структурная схема квадратурного демодулятора, реализованного в цифровом виде, приведена на рисунке 11.3.1. 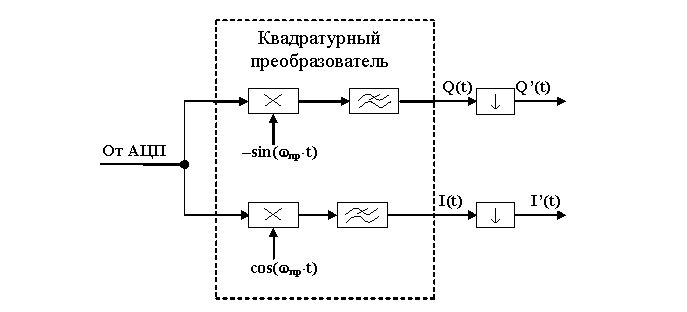 Рисунок 11.3.1 Структурная схема квадратурного демодулятора. Для формирования сигналов синуса и косинуса принимаемой частоты обычно применяется цифровой генератор. После ограничения преобразованного по частоте сигнала по спектру, появляется возможность уменьшить частоту его дискретизации. Поэтому на выходе фильтров низкой частоты ставятся дециматоры. Обычно операции децимации и фильтрации удобно выполнять в одном устройстве. Такие устройства получили название децимирующих фильтров. Глава 11 Децимирующие цифровые фильтры. Децимирующий фильтр предназначен для уменьшения частоты дискретизации обрабатываемого сигнала. Формально это можно было бы сделать, просто передавая на выход схемы каждый пятый или каждый второй отсчет входного сигнала. Устройство, выполняющее данную задачу, называется дециматором. Задача усложняется тем, что сигнал на входе дециматора не должен содержать спектральных составляющих в полосе образов выходного полезного сигнала. Поэтому прежде чем выбрасывать лишние отсчеты входного сигнала его следует ограничить по полосе. Существует ряд факторов, которые приводят к тому, что задача реализации фильтра-дециматора является трудной задачей. Первое это то, что входной поток данных поступает на вход этого фильтра с очень высокой скоростью. Фильтр должен выполнять вычисления в реальном времени с очень высокой скоростью. Частоты в полосе за пределами рабочей полосы сигнала должны быть подавлены до заданного уровня, определяемого динамическим диапазоном полезного сигнала. При этом в полосе рабочего сигнала фильтр-дециматор не должен вносить амплитудных или частотных искажений. Кроме того, структура фильтра должна быть простой и он должен легко реализовываться в интегральном исполнении. Децимирующий фильтр с конечной импульсной характеристикой На рисунке 11.3.2 приведен пример амплитудно-частотной характеристики децимирующего фильтра. Этот фильтр способен подавить мешающие сигналы в полосе трех высокочастотных образов полезного сигнала.  То, что фильтр пропускает на выход только четвертую часть входного спектра, означает, что на выходе подобного фильтра можно снизить частоту дискретизации сигнала в четыре раза. Глава 12 Однородные децимирующие цифровые фильтры. Наиболее просто в цифровом виде реализовать рассмотренный нами ранее однородный фильтр, так как для его реализации не требуются умножители. Для однородного фильтра четвертого порядка эта формула выглядит следующим образом:
Структурная схема фильтра, реализующего формулу (1), приведена на рисунке 11.3.3. 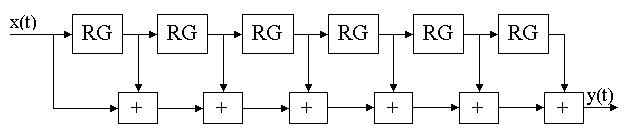 Рисунок 11.3.3. Структурная схема однородного фильтра седьмого порядка При реализации такого фильтра потребуется 6 сумматоров. Во столько же раз уменьшится быстродействии цифрового фильтра. Можно несколько видоизменить структуру данного фильтра. Для сокращения количества выполняемых операций формула 1 может быть переписана в следующем виде:
Эта формула может быть реализована за два действия:
В таком случае для реализации фильтра потребуется два каскада. Первый каскад будет выполнять интегрирование, а второй — фильтр с конечной импульсной характеристикой всего с двумя ненулевыми коэффициентами, равными единице. Структурная схема нового фильтра приведена на рисунке 11.3.4.  Рисунок 11.3.4. Структурная схема двухкаскадного фильтра, эквивалентного фильтру, приведенному на рисунке 11.3.3. В этой схеме максимальное время задержки сигнала определяется быстродействием сумматора и временем записи в регистр. Мы увеличили быстродействие почти в семь раз. Ну а теперь вспомним, для чего нам потребовался фильтр. Правильно. Для уменьшения количества отсчетов в единицу времени. Так как операция децимации линейна, то вторую часть фильтра мы можем перенести на выход дециматора. При таком схемном решении для формирования того же самого значения времени задержки нам потребуется только один регистр, так как на его вход тактовой синхронизации будет поступать частота в шесть раз меньше, чем частота синхронизации первого регистра. Получившаяся в результате всех преобразований структурная схема фильтра-дециматора приведена на рисунке 11.3.5. 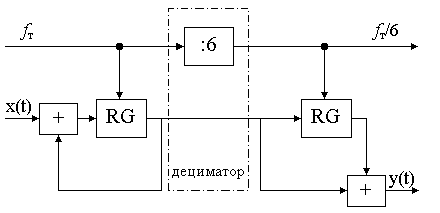 Рисунок 11.3.5. Структурная схема фильтра-дециматора, эквивалентного фильтру, приведенному на рисунке 11.3.3 Новая схема содержит всего два регистра и два двоичных сумматора, то есть данная схема получилась в три раза проще схемы однородного фильтра, приведенной на рисунке 11.3.4. Получившийся в результате преобразований фильтр трудно назвать однородным, однако для того, чтобы отобразить особенности его импульсной и амплитудно-частотной характеристик, сохраним название "однородный" и для этого фильтра.. Если по техническому заданию требуется еще больший коэффициент децимации по сравнению с рассмотренным выше случаем, то выигрыш при реализации однородного фильтра-дециматора по схеме, приведенной на рисунке 11.3.5, будет еще большим. Хотелось бы напомнить, что при анализе характеристик однородного фильтра для получения приемлемого уровня подавления мешающего сигнала нам потребовалось включить друг за другом несколько каскадов. Давайте включим последовательно друг за другом три фильтра-дециматора, как это показано на структурной схеме однородного фильтра, приведенной на рисунке 11.3.6. 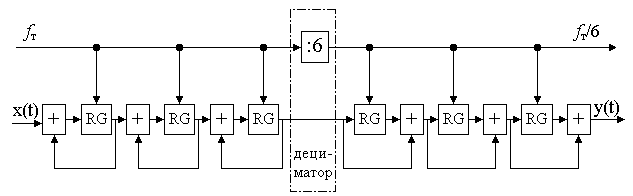 Рисунок 11.3.6. Структурная схема трехкаскадного фильтра-дециматора На рисунке 11.3.7 приведена амплитудно-частотная характеристика четырехкаскадного однородного фильтра. Обратите внимание, что образ полезного сигнала сосредоточен около выходной частоты дискретизации.  Рисунок 11.3.7. Амплитудно-частотная характеристика четырехкаскадного однородного фильтра-дециматора Проанализировав амплитудно-частотную характеристику четырехкаскадного однородного фильтра можно определить, что этот фильтр обладает максимальным подавлением мешающих сигналов именно в полосе частот высокочастотных образов полезного сигнала. Четырехкаскадный однородный фильтр может обеспечить подавление мешающих сигналов, находящихся в зоне высокочастотных образов полезного сигнала до 90 дБ, что вполне достаточно для реализации 16-разрядного представления полезного сигнала. Раздел 12 Примеры реализации цифровых устройств 12.1 Электронные часы Разработка структурной схемыПроанализируем как должно работать разрабатываемое устройство. Часы обязательно должны содержать устройство измерения времени, которое в свою очередь всегда состоит из генератора эталонных интервалов времени и счётчика этих интервалов. Структурная схема устройства измерения времени приведена на рисунке 12.1.1.  Рисунок 12.1.1 Структурная схема устройства измерения времени В качестве генератора эталонных импульсов в различное время использовали различные устройства. Это и вытекание воды или песка из какой-либо ёмкости и движение тени от солнца по циферблату и даже горение нити в огненных китайских часах. В простейшем случае генератор импульсов эталонной длительности должен вырабатывать минутные импульсы. В простейшем случае генератор импульсов эталонной длительности должен вырабатывать минутные импульсы. Однако реализовать стабильный генератор такой длительности достаточно сложно. Даже в механических часах в качестве генератора импульсов эталонной длительности использовался маятник с периодом колебаний от одной до нескольких секунд. В качестве генератора эталонных импульсов мог бы подойти кварцевый генератор, так как этот тип генераторов обладает высокой стабильностью колебаний. Но кварцевые генераторы вырабатывают колебания в диапазоне от 1 до 30 МГц. Это соответствует временным интервалам от 0.03 до 1 мкС. Тем не менее, если воспользоваться делителем частоты, выполненном на двоичном счетчике, то можно получить импульсы с периодом 1 минута. Выберем частоту работы кварцевого генератора. Здесь можно использовать кварцевый резонатор с частотой 32768Гц, предназначенный для использования в часах. Этот резонатор специально разрабатывался для применения в часах, поэтому его частота кратна степени двойки (215 = 32768). В результате можно использовать обычный двоичный делитель. Здесь хотелось бы отметить, какая грандиозная задача была решена разработчиками кварцевых кристаллов. Дело в том, что если посчитать длину акустической волны в кварце, то кварцевый резонатор получился бы впечатляющих размеров. Толщину кристалла кварца можно определить по общеизвестной формуле для длины волны. Как известно скорость распространения звуковой волны в кристалле кварца равна 5570м/с, тогда длина волны будет равна: L = v/f = 5570/32768 = 17см где v - это скорость звука в кристалле кварца; f - резонансная частота. То есть толщина кварцевого резонатора должна быть как минимум равна половине длины волны - 8,5см. Ну, как, впечатляет? Длина кварцевого кристалла соответственно должна быть, по крайней мере, в пять раз больше. Казалось бы, это неразрешимая проблема для малогабаритных и дешёвых устройств, однако разработчики кварцевого резонатора сумели решить её. Первым решением проблемы является то, что низкочастотные кварцевые резонаторы изготавливаются с использованием не объемных, а поверхностных волн. Точнее крутильных колебаний. В результате в резонаторе используется вся его длина. Скорость распространения волны по поверхности кварца значительно ниже скорости распространения волны в его объеме и равна 3515м/с. Однако даже в этом случае размеры кварцевого резонатора получаются значительными: L = v/f = 3515/32768 = 10,7см где v - это скорость звука в кристалле кварца; f - резонансная частота. Решением проблемы оказалась разработка кварцевого резонатора, реализованного по принципу камертона. В таком резонаторе возбуждаются не объемные колебания, а колебания двух параллельно расположенных стержней, как это показано на рисунке 12.1.2.  В такой конструкции частота резонанса зависит от упругости кварца, длины и толщины зубьев получившейся вилки камертона. Стоимость часовых кварцевых резонаторов оказалась минимальной из всех кварцевых резонаторов. Благодаря своей распространённости, малой цене, габаритам и малой частоте часовые кварцевые резонаторы начинают применяться практически во всех цифровых устройствах. Для нас полезными свойствами часового кварцевого резонатора является малая цена, малые габариты, кратность частоты одному герцу и относительно малая частота резонанса. Последнее свойство определяет частоту задающего генератора, и, как следствие, малое потребление тока этим генератором от источника питания. Итак, для формирования секундных импульсов (частота 1 Гц) потребуется делитель частоты на 32768. Для формирования из секундных импульсов минутных импульсов потребуется ещё один делитель частоты. Так как в минуте содержится 60 секунд, то нам потребуется делитель на 60. Уточнённая структурная схема разрабатываемого цифрового устройства приведена на рисунке 12.1.2.  Рисунок 12.1.2. Уточнённая структурная схема устройства измерения времени Теперь займёмся схемой счётчика временных интервалов. Он будет состоять из счетчика минут и счётчика часов. Мы знаем, что счётчик минут должен работать по основанию 60. В то же самое время мы привыкли воспринимать числа в десятичной системе счисления. Поэтому будет удобно разбить счётчик минут на два счётчика: на десятичный счётчик и счётчик, считающий до шести. Счетчик часов можно выполнить по основанию 12 и по основанию 24. Пусть в наших часах счётчик будет работать по основанию 24. При этом для удобства отображения информации, также как и в счётчике минут, реализуем его на двух десятичных счетчиках. Следующий блок, который обязательно должен входить в состав часов — это устройство индикации. Ведь никого не устроят часы, которые будут точно отсчитывать время, но при этом мы не сможем увидеть результат! Выберем в качестве устройства отображения времени светодиодные семисегментные индикаторы. В этом случае мы получим устройство, способное работать при отрицательной температуре и обладающее при этом наиболее простой схемой. Для преобразования кода, в котором работает счётчик минутных импульсов, в семисегментный код нам потребуетсядешифратор. То есть, блок индикации будет состоять из дешифраторов и собственно индикаторов. Уточнённая структурная схема часов приведена на рисунке 12.1.3.  Рисунок 12.1.3. Структурная схема часов И, наконец, последнее замечание. Любые часы время от времени требуют коррекции своего значения с целью синхронизации своих показаний с всемирным временем. В нашей схеме это будет делать блок коррекции, который в свою очередь будет состоять из кнопок и схемы установки внутреннего состояния счётчика временных интервалов. На этом можно завершить разработку структурной схемы. Полная структурная схема часов с учётом блока индикации и блока коррекции времени приведена на рисунке 12.1.4. 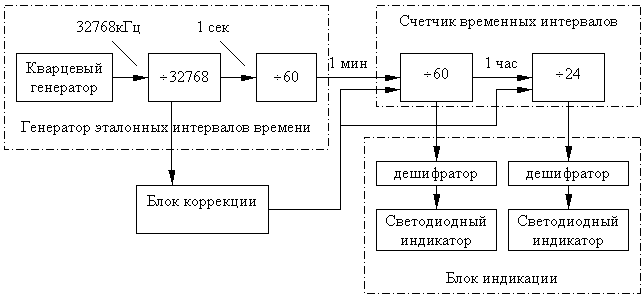 Рисунок 12.1.4. Уточнённая структурная схема часов Теперь, после того как составлена структурная схема часов, можно приступить к разработке их принципиальной схемы. |
