ла слау. ЛА-СЛАУ-УсловияЗаданий-1. Дана Система Линейных Алгебраических Уравнений. Требуется решить её тремя способами 1) Решить её методом Гаусса (исключения неизвестных элементарными преобразованиями матрицы) Проверить решение
 Скачать 247 Kb.
|
1. ПРИМЕР Решения СЛАУ методом Гаусса (исключения неизвестных элементарными преобразованиями расширенной матрицы системы).Метод Гаусса – это метод последовательного исключения неизвестных. Суть метода применительно к системе 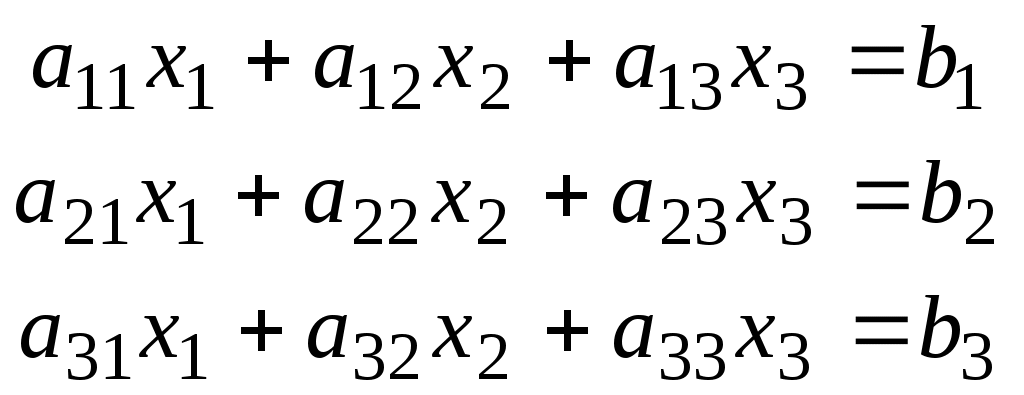 состоит в поочередном исключении неизвестных из уравнений, «перебираемых сверху вниз», а затем в вычислении переменных «снизу вверх»: 1. Прямой ход метода Гаусса Переменная  выражается из первого уравнения через переменные x2, x3; Полученное выражение для x1 подставляется во 2-е и 3-е уравнения вместо ;Таким образом переменная исключается из 2-го и 3-го уравнений.Переменная x2 выражается из 2-го уравнения через переменную x3; Полученное выражение для x2 подставляется в 3-е уравнения вместо x2. Таким образом переменная x2 исключается из 3-го уравнения. В результате система преобразуется в равносильную ей систему треугольного вида (с другими коэффициентами и правыми частями, но с теми же решениями): 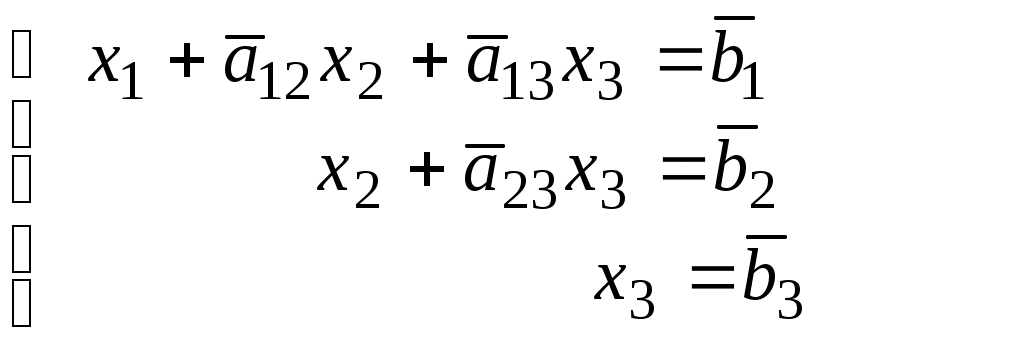 2. Обратный ход метода Гаусса. Значения неизвестных вычисляются из системы треугольного вида при «движении снизу вверх»: 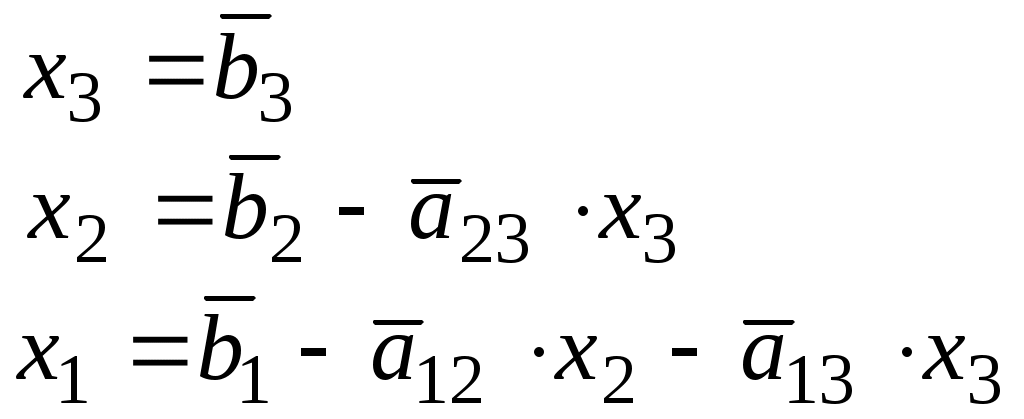 .При решении систем линейных уравнений удобно работать не с самой системой, а с ее расширенной матрицей. Исключение неизвестных «на языке матриц» проводится с помощью т.н. элементарных преобразований матриц. В методе Гаусса в основном применяется следующее элементарное преобразование: (1) Прибавление к одной строке матрицы другой строки, умноженной на число; (соответствует прибавлению к одному уравнению системы другого). Это преобразование используется для «зануления» нужного элемента строки. Иногда необходимо преобразование (2) Перестановка строк матрицы (соответствует перестановке уравнений в системе). Это преобразование используется, чтобы на нужное место строки поставить ненулевой элемент. Далее в примере решения СЛАУ используется преобразование (1) – сложение строк.
Выпишем матрицу коэффициентов СЛАУ, столбец правых частей и столбец неизвестных: (матрицы и столбцы ниже заключены в квадратные скобки)
Применим к матрице следующие элементарные преобразования: Прибавим ко 2-й строке 1-ю строку, умноженную на -2; прибавим к 3-й строке 1-ю строку, умноженную на -3 (первая строка не меняется):
Говоря на языке уравнений мы исключили первую переменную из уравнений 2 и 3.
В системе появилась подсистема из 2-х уравнений №2 и 3 с двумя неизвестными x2 и x3. Применим к получившейся матрице элементарное преобразование: прибавим к 3-й строке 2-ю строку, умноженную на 5: (первая и вторая строка не меняется):
Говоря на языке уравнений мы исключили вторую переменную из уравнения 3. Преобразованной матрице соответствует преобразованная СЛАУ: 1*x1 + 1*x2 + 5*x3 = 0 0*x1 + 1*x2 + (-6)*x3 = 8 0*x1 + 0*x2 + (-41)*x3 = 41 или x 1 + x2 + 5x3 = 0 x2 – 6x3 = 8 – 41 x3 = 41 Выполним обратный ход метода Гаусса для определения значений неизвестных из уравнений «снизу вверх»: x 3 = 41/(-41) = –1 x 2 = 8 + 6x 3 = 8 + 6*(– 1) = 8 – 6 = 2 x 1 = 0 – x 2 – 5x 3 = –2 – 5(–1) = –2 + 5 = 3
Проверка Проверим решение подстановкой в уравнения исходной системы. 1-е уравнение системы: x1 + x2 + 5x3 = 0 Подставляем значения неизвестных в левую часть: 3 + 2 + 5*(–1) = 2+3 – 5 = 0 - получаем правую часть уравнения. 2-е уравнение системы: 2x1 + 3x2 + 4x3 = 8 Подставляем значения неизвестных в левую часть: 2*3 + 3*2 + 4*(-1) = 6 + 6 – 4 = 12 – 4 = 8 - получилась правая часть уравнения. 3-е уравнение системы: 3 x1 – 2 x2 + 4 x3 = 1. Подставляем значения неизвестных в левую часть: 3*3 – 2*2 + 4*(–1) = 9 – 4 – 4 = 1 - получаем правую часть уравнения.
|