!Антикризисное. Диагностика банкротства и финансового состояния предприятия
 Скачать 120.68 Kb. Скачать 120.68 Kb.
|
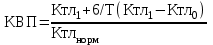 где: Ктл1 и Ктл0 – соответственно фактическое значение коэффициента ликвидности в конце и начале отчетного периода; Ктлнорм – нормативное значение коэффициента текущей ликвидности; 6 – период восстановления платежеспособности, мес.; Т – отчетный период, мес. 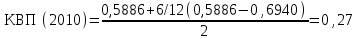 Так как КВП1, ОАО «РЖД» не имеет реальной возможности восстановить свою платежеспособность. 2.2 Интегральный подход западных экономистов Проведем анализ вероятности банкротства с помощью двухфакторной – Z-модели. При этом в качестве ключевых показателей используются коэффициент текущей ликвидности (степени покрытия краткосрочных пассивов, оборотными активами), и коэффициента финансовой зависимости (Кфз – доли заемных средств в совокупных пассивах организации). Двухфакторная модель в практике американской аналитиков имеет вид: Z= -0,3877 – 1,0736*Ктл + 0,0579*Кфз Кфз (2018) = 285615818/3171157697= 0,0901 Кфз (2019) = 564845365/3505173897= 0,1611 Кфз (2020) = 703403824/3675295787= 0,1914 Z (2018) = -0,3877 – 1,0736 × 0,7724+ 0,0579 × 0,0901 = -1,2112 Z (2019) = -0,3877 – 1,0736 × 0,6940 + 0,0579 × 0,1611 = -1,1235 Z (2020) = -0,3877 – 1,0736 × 0,5886+ 0,0579 × 0,1914= -1,0085 Значение Z, рассчитанное по показателям отрицательное, поэтому вероятность банкротства ОАО «РЖД» в течение ближайшего года невелика. Недостаток двухфакторной модели состоит в том, что многообразие финансовых процессов не всегда отражается в коэффициентах платежеспособности, используемых в качестве ключевых показателей модели. Следовательно, рассмотренная двухфакторная модель не обеспечивает всестороннюю оценку финансового состояния предприятия, поэтому возможны значительные отклонения прогноза от реальности. Помимо двухфакторной модели существует четырехфакторная дискриминантная модель, разработанная Дж. Блиссом: Z = 0,063*X1 + 0,092*X2 + 0,057*X3 + 0,001*X4 где X1 = Оборотный капитал / Сумма активов, X2 = Прибыль от реализации / Сумма активов, X3 = Чистая прибыль / Сумма активов, X4 = Собственный капитал / Заемный капитал. В данной модели предельным значением Z является 0,037: при значении Z больше 0,037 вероятность банкротства мала, при значении Z меньше указанного предела вероятность банкротства велика. Проведем расчет четырехфакторной модели по данным 2019 и 2020 гг. X1 (2019) = 263155432/3505173897 = 0,0751 X2 (2019) = 66391516/3505173897 = 0,0189 X3 (2019) = 13400339/3505173897 = 0,0038 X4 (2019) = 2940328532/564845365 = 5,2055 X1 (2020) = 205043346/3675295787 = 0,0558 X2 (2020) = 50221394/3675295787= 0,0137 X3 (2020) = 14447393/3675295787 = 0,0039 X4 (2020) = 2971891963/703403824 = 4,2250 Z(2019) = 0,063*0,0751+0,092*0,0189+0,057*0,0038+0,001*5,2055 = 0,0119 Z(2020) = 0,063*0,0558+0,092*0,0137+0,057*0,0039+0,001*4,2250 = 0,0092 Таким образом, можно сделать вывод, что вероятность банкротства предприятия велика. Недостатком четырехфакторных моделей является то, что в них не учитываются коэффициенты финансовой устойчивости и рыночной активности предприятия. Пятифакторная Модель Z-счета Альтмана получила наибольшее распространение в странах с развитой рыночной экономикой. Модель построена с помощью аппарата мультипликативного дискриминантного анализа и в первом приближении позволяет разделить хозяйствующих субъектов на потенциальных банкротов и не банкротов. Пятифакторная модель Альтмана для акционерных обществ, чьи акции котируются на рынке имеет вид: Z = 1,2*Х1+1,4*Х2 + 3,3*Х3 + 0,6*Х4+Х5 где X1 = Собственные оборотные средства/Сумма активов, X2 = Резервный капитал + нераспределенная прибыль/Сумма активов, X3 = Прибыль до налогообложения и выплаты процентов / Сумма активов, X4 = Собственный капитала (в балансовой оценке) / Заемный капитал, X5 = Выручка-нетто / Сумма активов. В результате подсчета Z – показателя для конкретного предприятия делается заключение: Если Z<1,81 – вероятность банкротства очень высокая (80 до 100%); Если Z находится в интервале от 1,81 до 2,77 – высокая вероятность банкротства (35 до 50%); Если Z находится в интервале от 2,77 до 2,99 – вероятность банкротства невелика (от 15 до 20%); Если Z более 2,99 – ситуация на предприятии стабильна, риск неплатежеспособности в течение ближайших двух лет крайне мал. Точность прогноза в этой модели на горизонте одного года составляет 95%, на два года – 83%, что является ее достоинством. Недостатком же этой модели заключается в том, что ее по существу можно рассматривать лишь в отношении крупных компаний, разместивших свои акции на фондовом рынке. Проведем расчет пятифакторной модели по данным 2019 и 2020 года. X1 (2019) = -301689933/3505173897 = -0,0861 X2 (2019) = (1218696+50997500)/3505173897 = 0,0149 X3 (2019) = 54774860/3505173897 = 0,0156 X4 (2019) = 2940328532/564845365 = 5,2055 X5 (2019) = 1101710458/3505173897 = 0,3143 Z(2019) = 1,2*(-0,0861)+1,4*0,0149 + 3,3*0,0156+0,6*5,2055+0,3143 = 3,4 X1 (2020) = -498360478/3675295787 = -0,1356 X2 (2020) = (2539196+136410172)/3675295787 = 0,0378 X3 (2020) = 60315227/3675295787 = 0,0164 X4 (2020) = 2971891963/703403824 = 4,2250 X5 (2020) = 1050157925/3675295787 = 0,2857 Z(2020) = 1,2*(-0,1356)+1,4*0,0378+3,3*0,0164+0,6*4,2250+0,2857 = 2,765 Таким образом, из полученных расчетов можно сделать вывод, что в 2019 году вероятность банкротства была ничтожна, так как рассчитанное значение превышает 2,99. В 2020 году значение Z составляет 2,765, что приблизительно составляет 2,77, поэтому можно значение отнести к группе от 2,77 до 2,99, где вероятность банкротства невелика (от 15 до 20%) 2.3 Анализ вероятности банкротства с использованием интегрального подхода российских экономистов (адаптированные модели) Некоторые российские экономисты считают, что использовать рассмотренные комплексные модели и, в частности, модели Альтмана в условиях переходной экономики для российских предприятий нецелесообразно по следующим основаниям: - несопоставимость факторов, генерирующих угрозу банкротства, - различия в учете отдельных показателей, - влияние инфляции на формирование показателей - несоответствие балансовой и рыночной стоимости отдельных активов и др. С целью диагностики возможного банкротства для условий функционирования российских предприятий Р.С. Сайфуллиным и Г.Г. Кадыковым была предложена модель расчета рейтингового числа: R = 2*K1 + 0,1*K2 + 0,08*K3 + 0,45*K4 + K5, где K1 = Собственные оборотные средства / Оборотные активы; K2 = Оборотные активы/Краткосрочные обязательства; K3 = Выручка-нетто/Сумма активов; K4 = Чистая прибыль (убыток)/Выручка; K5 = Чистая прибыль (убыток)/Собственный капитал. Если расчетное значение рейтингового числа превышает единицу, то для такой организации банкротство маловероятно, в противном случае финансовое состояние предприятия характеризуется как неудовлетворительное и ему может угрожать банкротство. Проведем расчет модели по данным 2019 и 2020 года. K1 (2019) = -301689933/263155432 = -1,1464 K2 (2019) = 263155432/379159947 = 0,6940 K3 (2019) = 1101710458/3505173897 = 0,3143 K4 (2019) = 13400339/1101710458 = 0,0122 K5 (2019) = 13400339/2940328532 = 0,0046 R(2019) = 2*(-1,1464)+0,1*0,6940+0,08*0,3143+0,45*0,0122+0,0046 = -2,1882 K1 (2020) = -498360478/205043346 = -2,4305 K2 (2020) = 205043346/348350133 = 0,5886 K3 (2020) = 1050157925/3675295787 = 0,2857 K4 (2020) = 14447393/1050157925 = 0,0138 K5 (2020) = 14447393/2971891963 = 0,0049 R(2020) = 2*(-2,4305)+0,1*0,5886+0,08*0,5886+0,45*0,0138+0,0049 = -4,7439 Таким образом, финансовое состояние ОАО «РЖД» характеризуется как неудовлетворительное и ему может угрожать банкротство. Рассчитаем модель прогноза риска банкротства, которая разработана учеными Иркутской государственной экономической академии. Модель R-счета (четырехфакторная модель) имеет следующий вид: R = 0,717*K1 + 0,847*K2 + 3,107*K3 + 0,420*K4, где K1 = Оборотные активы/Сумма активов, K2 = Чистая прибыль (убыток)/Собственный капитал, K3 = Выручка-нетто/Сумма активов, K4 = Чистая прибыль (убыток)/Суммарные затраты по продажам (себестоимость). Взаимосвязь вероятности банкротства с численным значением R-счета представлена в таблице 7. Достоинством данной модели является то, что ее разработка производилась по данным отечественных организаций. Таблица 7 – Оценка вероятности банкротства по значению R-счета
|
