Математическое и имитационное моделирование (текст). Экономическими моделями

• Название: Экономическими моделями
• Дата: 25.04.2023
• Размер: 0.83 Mb.
• Имя файла: Математическое и имитационное моделирование (текст).docx
• Тип: Документы; #1089528
• страница: 9 из 9

Пример 15. Фирма производит детские платья и костюмы, реализация которых зависит от состояния погоды. Затраты фирмы в течение августа – сентября на единицу продукции составили: платья – 7 ден. ед., костюма – 28 ден. ед. Цена реализации составляет 15 и 50 ден. ед., соответственно.

По данным наблюдений за несколько предыдущих лет, фирма может реализовать в условиях теплой погоды 1950 платьев и 610 костюмов, а при прохладной погоде 630 платьев и 1050 костюмов.

В связи с возможными изменениями погоды определим стратегию фирмы в выпуске продукции, обеспечивающую ей максимальный доход от реализации продукции. Задачу решим с использованием критериев природы, приняв λ = 0,5.

▲ Фирма располагает двумя стратегиями:

• А₁ – в этом году будет теплая погода;

• А₂ – погода будет прохладная.

Возможные состояния природы:

• В₁– будет теплая погода;

• В₂ – будет прохладная погода.

Доход фирмы (ден. ед.) составит:

• при выборе стратегии А₁ и состоянии погоды В₁

1950∙(15 -7) + 610∙(50 - 28) = 29020;

• при выборе стратегии А₁ и состоянии погоды В₂

630∙(15 - 7) + 610∙(50 - 28) - 7∙(1950 - 630) = 9220;

• при выборе стратегии А₂ и состоянии погоды В₁

630∙(15 - 7) + 610∙(50 - 28) - 28∙(1050 - 610) = 6140;

• при выборе стратегии А₂ и состоянии погоды В₂

630∙(15 - 7) + 1050∙(50 - 28) = 28140.

Рассматривая фирму и погоду в качестве двух игроков, запишем платежную матрицу со столбцами M_i, α_i, ω_i, γ_i.

	В1	В2	Mi	αi	ωi	γi
А1 А2	29020 6140	9220 28140	19120* 17140	9220* 6140	29020* 28140	19120* 17140

Рассмотрим использование различных критериев природы.

Критерий Лапласа: max M_i = 19120, т.е. фирме целесообразно использовать стратегию А₁.

Критерий Вальда: 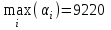, т.е. фирме целесообразно использовать стратегию А₁.

Критерий максимума: 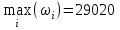, т.е. фирме целесообразно использовать стратегию А₁.

Критерий Гурвица: 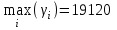, т.е. фирме целесообразно использовать стратегию А₁.

Критерий Сэвиджа. Запишем матрицу риска r_ij со столбцом δ_i:

	В1	В2	δi
А1 А2	0 22880	18920 0	18920* 22880

Так как min δ_i = 18920, то фирме целесообразно использовать стратегию А₁.

Оптимальной по всем критериям является стратегия А₁.

Таким образом, фирме целесообразно производить 1950 платьев и 610 костюмов, тогда при любой погоде она получит доход не менее 9220 д. ед.▲

Принятие решений в условиях риска

Математическая модель задачи принятия решений в условиях риска предполагает задание дополнительной информации о поведении «природы» в виде вероятностей ее различных состояний.

Когда состояниям природы поставлены в соответствие вероятности, заданные экспертно либо вычисленные, решение обычно принимается на основе критерия максимума ожидаемого среднего выигрыша или минимума ожидаемого среднего риска.

Если для некоторой игры с природой, задаваемой платежной матрицей (a_ij)_mn, стратегиям природы П соответствует вектор вероятности p = (p₁, p₂,…, p_n) состояний среды, то лучшей стратегией игрока А будет та, которая обеспечит ему максимальный средний выигрыш, т.е.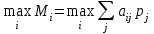



Применительно к матрице рисков лучшей будет та стратегия игрока, которая обеспечивает ему минимальный средний риск, т.е.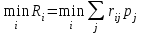



Эти критерии эквивалентны в том смысле, что оптимальные значения для них обеспечивает одна и та же стратегия игрока А.

Пример 16. Пусть платежная матрица и вероятности состояния среды представлены таблицей

Стратегия игрока A	Вероятность различных состояний среды				Mi
	0,4	0,2	0,2	0,2
А1 А2 А3 А4	5 2 8 1	2 3 5 4	8 4 3 2	4 12 10 8		4,8 4,6 6,8 3,2

▼ В столбце M_iтаблицы указаны .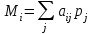

Поскольку 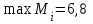, то А₃ – лучшая стратегия игрока А.

Матрица риска, соответствующая искомой платежной матрице:

Стратегия игрока A	Вероятность различных состояний среды				Ri
	0,4	0,2	0,2	0,2
А1 А2 А3 А4	3 6 0 7	3 2 0 1	0 4 5 6	8 0 2 4	3,4 3,6 1,4 5

В столбце R_iтаблицы указаны .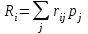

Поскольку 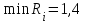, то А₃ – лучшая стратегия игрока А▲
Дерево решений

Рассмотренные нами критерии принятия решений позволяют делать вывод из совокупности так называемых одноэтапных альтернатив. При этом подразумевается, что решения, принимаемые в будущем, не зависят от решений, принимаемых в текущий момент.

Рассмотрим многоэтапный процесс принятия решений, в котором взаимозависимые решения принимаются последовательно. Графически подобные процессы могут быть представлены с помощью дерева решений. Такое представление облегчает описание процесса принятия решений.

Дерево решений – это графическое изображение процесса принятия решений, в котором отражены альтернативные решения, альтернативные состояния среды, соответствующие вероятности и выигрыш для любых комбинаций альтернатив и состояний среды.

Дерево решений состоит из ряда узлов (квадраты, круги) и исходящих из них ветвей (линий). Рисуют деревья слева направо.

При формировании дерева используются следующие обозначения: квадраты - места принятия решений; круги - места появления исходов; пунктирные линии - возможные решения; сплошные линии - возможные исходы.

Ожидаемая денежная оценка (ОДО) – это средний выигрыш в игре, он рассчитывается как сумма произведений размеров выигрышей на вероятности этих выигрышей.

Процедура принятия решения заключается в вычислении для каждой вершины дерева (при движении справа налево) ожидаемых денежных оценок (ОДО), отбрасыванием неперспективных ветвей и выборе ветвей, которым соответствует максимальное значение ОДО.

Пример. Предприятие решает вопрос, какую назначить цену на свой товар: 40 руб. или 50 руб. Если будет установлена цена 40 руб., то возможны следующие варианты объема продаж: 40000 руб. с вероятностью 0,2; 35000 руб. с вероятностью 0,3 и 30000 руб. с вероятностью 0,5. Если будет установлена цена 50 руб., то возможны следующие варианты объема продаж: 36000 руб. с вероятностью 0,1; 33000 руб. с вероятностью 0,5 и 31000 руб. с вероятностью 0,4. Определим с помощью дерева решений, какую цену следует назначить предприятию на свой товар. Какова ожидаемая денежная оценка наилучшего решения?

▼ На основе данных примера строим дерево решений, рис.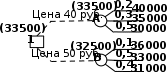



Ожидаемые денежные оценки:

 узел А: ОДО_А = 0,240000 + 0,335000 + 0,530000 = 33500 руб. Это число пишем над узлом А;

 узел В: ОДО_В = 0,136000 + 0,533000 + 0,431000 = 32500 руб. Это число пишем над узлом В;

 узел 1: ОДО₁ = max{ОДО_А, ОДО_B}= max{33500, 32500}=33500 = ОДО_А. Эту оценку пишем над узлом 1, а решение «назначить цену 50 руб.» отбрасываем.

Ожидаемая денежная оценка наилучшего решения равна 33 500 руб. Предприятию следует назначить цену 40 руб.

Упражнение. Предприятие решает вопрос, какую назначить цену на свой товар: 60 руб. или 70 руб. Если будет установлена цена 60 руб., то возможны следующие варианты объема продаж: 50000 руб. с вероятностью 0,3; 45000 руб. с вероятностью 0,4 и 40000 руб. с вероятностью 0,3. Если будет установлена цена 70 руб., то возможны следующие варианты объема продаж: 46000 руб. с вероятностью 0,2; 43000 руб. с вероятностью 0,4 и 41000 руб. с вероятностью 0,4. Определим с помощью дерева решений, какую цену следует назначить предприятию на свой товар. Какова ожидаемая денежная оценка наилучшего решения?

Ответ: 60 руб. и 45000 руб.