Математическое и имитационное моделирование (текст). Экономическими моделями

• Название: Экономическими моделями
• Дата: 25.04.2023
• Размер: 0.83 Mb.
• Имя файла: Математическое и имитационное моделирование (текст).docx
• Тип: Документы; #1089528
• страница: 1 из 9

Введение

Моделирование – основной метод исследования во всех областях знаний и научно обоснованный метод оценок сложных систем, используемых для принятия решений во всех сферах человеческой деятельности.

Для изучения различных экономических явлений экономисты используют их упрощенные формальные описания, называемые экономическими моделями. При построении экономических моделей выявляются существенные факторы и отбрасываются несущественные для решения поставленной задачи детали.

Моделью называется объект-заместитель, который в определенных условиях может заменить объект-оригинал, воспроизводя интересующие исследователя свойства оригинала.

Метод исследования, базирующийся на разработке и использовании моделей, называется моделированием. Модель называется адекватной объекту, если результаты моделирования подтверждаются и могут служить основой для прогнозирования процессов, протекающих в исследуемых объектах.

Необходимость моделирования обусловлена сложностью, а порой и невозможностью прямого изучения реального объекта (процесса). Значительно доступнее создавать и изучать модели реальных объектов (процессов). Эти модели отражают существенные свойства реального объекта (процесса), хотя на самом деле действительность значительно содержательнее и богаче. 

Особую роль в науке играют математические модели.

Математическая модель — это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики

Математическое моделирование – это средство изучения реального объекта, процесса или системы путем их замены математической моделью, более удобной для экспериментального исследования с помощью ЭВМ. Математическая модель является приближенным представлением реальных объектов, процессов или систем, выраженным в математических терминах и сохраняющим существенные черты оригинала. Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи.

По принципам построения математические модели разделяют на аналитические и имитационные.

В аналитических моделях процессы функционирования реальных объектов, процессов или систем записываются в виде явных функциональных зависимостей. Однако по мере усложнения объекта моделирования построение аналитической модели превращается в трудноразрешимую проблему. Тогда исследователь вынужден использовать имитационное моделирование.

Имитационное моделирование – это метод исследования, заключающийся в имитации на ЭВМ процесса функционирования системы или отдельных ее частей и элементов. Сущность метода имитационного моделирования заключается в разработке таких алгоритмов и программ, которые имитируют поведение системы, ее свойства и характеристики в необходимом для исследования системы составе, объеме и области изменения ее параметров.

Имитационные модели достаточно просто учитывают влияние случайных факторов. При наличии случайных факторов необходимые характеристики моделируемых процессов получаются многократными прогонами (реализациями) имитационной модели и дальнейшей статистической обработкой накопленной информации. Поэтому часто имитационное моделирование процессов со случайными факторами называют статистическим моделированием.

В управлении хозяйственными процессами наибольшее значение имеют прежде всего экономико-математические модели, часто объединяемые в системы моделей.

Экономико-математическая модель — это математическое описание экономического объекта или процесса с целью их исследования и управления ими. Она представляет собой концентрированное выражение общих взаимосвязей и закономерностей экономического явления в математической форме.

Экономико-математические методы — обобщающее название комплекса экономических и математических научных дисциплин, объединенных для изучения экономики. В процессе использования экономико-математических методов в экономическом анализе осуществляется построение и изучение экономико-математических моделей, описывающих влияние отдельных факторов на обобщающие экономические показатели деятельности организаций.

Процесс экономико-математического моделирования можно разделить на несколько основных этапов.

1. Постановка экономической проблемы и ее качественный анализ. Этот этап включает выделение важнейших черт и свойств моделируемого объекта; изучение структуры объекта и основных зависимостей, связывающих его элементы; формулирование гипотез, объясняющих поведение и развитие объекта.

2. Построение математической модели. Это этап формализации экономической проблемы, формулирования ее в виде конкретных математических зависимостей и отношений (функций, уравнений, неравенств и т. д.). Как правило, сначала определяется тип математической модели, а затем уточняются детали.

3. Математический анализ модели. Целью этого этапа является выяснение общих свойств модели. Здесь применяются чисто математические приемы исследования. Если удается доказать, что математическая задача не имеет решения, то необходимость в последующей работе по первоначальному варианту модели отпадает, и следует скорректировать либо постановку экономической задачи, либо способы ее математической формализации. При аналитическом исследовании модели выясняются вопросы: единственно ли решение, какие переменные (неизвестные) могут входить в решение, каковы будут соотношения между ними, в каких пределах и в зависимости от каких исходных условий они изменяются, каковы тенденции их изменения и т. д.

4. Подготовка исходной информации. Математическое моделирование предъявляет жесткие требования к системе информации; при этом надо принимать во внимание не только принципиальную возможность подготовки информации требуемого качества, но и затраты на подготовку информационных массивов. В процессе подготовки информации используются методы теории вероятностей, теоретической и математической статистики для организации выборочных обследований, оценки достоверности данных и т.д. При системном экономико-математическом моделировании результаты функционирования одних моделей служат исходной информацией для других.

5. Численное решение. Этот этап включает разработку алгоритмов для численного решения задачи и непосредственное проведение расчетов. Исследование, проводимое численными методами, может существенно дополнить результаты аналитического исследования, а для многих моделей оно является единственно осуществимым.

6. Анализ численных результатов и их применение. На этом заключительном этапе встает вопрос о правильности и полноте результатов моделирования, о степени практической применимости последних. Математические методы проверки могут выявлять некорректные построения модели и тем самым сужать класс потенциально правильных моделей. Неформальный анализ теоретических выводов и численных результатов, получаемых с помощью модели, сопоставление их с имеющимися знаниями и фактами действительности также позволяют обнаруживать недостатки постановки экономической задачи, сконструированной математической модели, ее информационного и математического обеспечения.
Линейное программирование

Линейное программирование – наука о методах исследования и отыскание наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения.

Функция, наибольшее и наименьшее значение которой отыскивается, называется целевой функцией.

Построим математические модели простейших экономических задач.

Пример 1 (задача об использовании ресурсов). Для изготовления двух видов продукции Р₁, Р₂ используются три вида ресурсов S₁, S₂, S₃. Запасы ресурсов, затраты ресурсов на единицу продукции, а также цены единицы продукции приведены в следующей таблице

Ресурсы	Затраты ресурсов на ед. продукции		Запасы ресурсов
	Р1	Р2
S1	2	4		2000
S2	4	1		1400
S3	2	1		800
Цена ед. продукции	40	60

Требуется построить план производства, максимизирующий доход.

Построим математическую модель задачи, определив в ней переменные, ограничения и целевую функцию.

Переменные: х₁, х₂ – количество единиц выпускаемой продукции Р₁, Р₂ (объемы производства).

Ограничения. Ограничение на расход ресурсов можно записать в следующем виде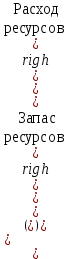

.

Это приводит к следующей системе ограничений:



Кроме того, переменные должны быть неотрицательными.

, - условие неотрицательности.

Целевая функция – суммарный доход от реализации всей продукции: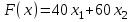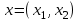

, .

Требуется найти такие неотрицательные переменные х₁, х₂, удовлетворяющие ограничениям, при которых суммарный доход максимален, т.е.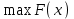

.

Экономико-математическая модель задачи кратко записывается в виде:



при ограничениях



, - условие неотрицательности.

Пример 2 (задача составления рациона). Норма пищевого рациона должна содержать не менее b₁, b₂, b₃ питательных веществ S₁, S₂, S₃. Для составления пищевого рациона используются два вида продуктов питания Р₁, Р₂. Содержание питательных веществ в единице каждого продукта и стоимость единицы продукта (цена) приведены в следующей таблице

Питательные вещества	Содержание питательных веществ в ед. продукта		Норма вещества
	Р1	Р2
S1	3	1	9
S2	1	2	8
S3	1	6	12
Цена ед. продукта	4	6

Требуется так составить пищевой рацион, чтобы обеспечить норму рациона при его минимальной стоимости.

Построим математическую модель задачи, определив в ней переменные, ограничения и целевую функцию.

Переменные: х₁, х₂ – количество единиц соответствующего вида продукта Р₁, Р₂.

Ограничения. Ограничение на содержание питательных веществ в рационе можно записать в следующем виде

.

Это приводит к следующей системе ограничений:



Кроме того, переменные должны быть неотрицательными.

, - условие неотрицательности.

Целевая функция – общая стоимость рациона: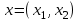

, .

Требуется минимизировать стоимость рациона при заданных ограничениях, т.е. .

Экономико-математическая модель задачи кратко записывается в виде



при ограничениях



, - условие неотрицательности.
Общая задача линейного программирования

Общая задача линейного программирования (ОЗЛП) ставится следующим образом. Найти экстремум (максимум или минимум) линейной целевой функции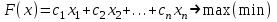



при ограничениях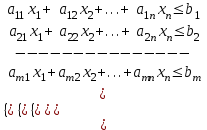



- условие неотрицательности,

где x_j – переменные; a_ij, b_i, c_j – заданные постоянные величины.

В системе ограничений неравенства могут быть направлены в ту или иную сторону (, ).

Допустимым решением (планом) ОЗЛП называется вектор x = (x₁, x₂,…, x_n), удовлетворяющий системе ограничений и условию неотрицательности.

Областью допустимых решений (ОДР) называется множество всех допустимых решений ОЗЛП.

Оптимальным решением ОЗЛП называется допустимое решение, при котором целевая функция достигает своего экстремального значения.
Геометрическая интерпретация ОЗЛП

Рассмотрим ОЗЛП с двумя переменными (на плоскости).



при ограничениях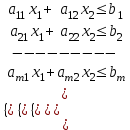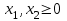



- условие неотрицательности.

Свойства решений ОЗЛП тесно связаны со свойствами выпуклых множеств. Рассмотрим на плоскости множество точек .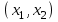

Множество точек на плоскости называется выпуклым, если оно вместе с любыми своими двумя точками содержит и весь отрезок, соединяющий их; в противном случае называется невыпуклым.

Примеры выпуклых и невыпуклых множеств показаны на рис.



Точка А называется внутренней точкой выпуклого множества, если в сколь угодно малой окрестности этой точки содержатся только точки этого множества.

Точка В называется граничной точкой выпуклого множества, если в сколь угодно малой окрестности этой точки содержатся как точки данного множества, так и не принадлежащие ему.

Точка С называется угловой точкой выпуклого множества, если она является граничной и не лежит внутри отрезка, соединяющего две другие точки этого множества.

Множество называется замкнутым, если оно включает все свои граничные точки.

Множество называется ограниченным, если существует окружность радиуса конечной длины с центром в любой точке множества, которое полностью содержит в себе данное множество; в противном случае называется неограниченным.

Пересечением выпуклых множеств называется множество, представляющее общую часть данных множеств.